Лекция №1 КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
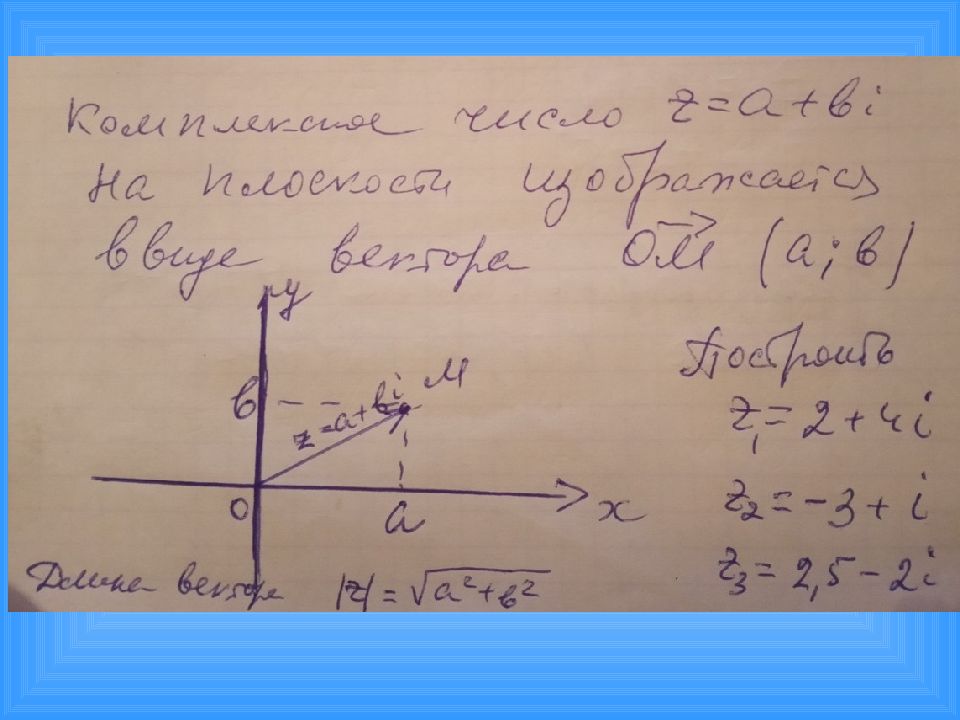
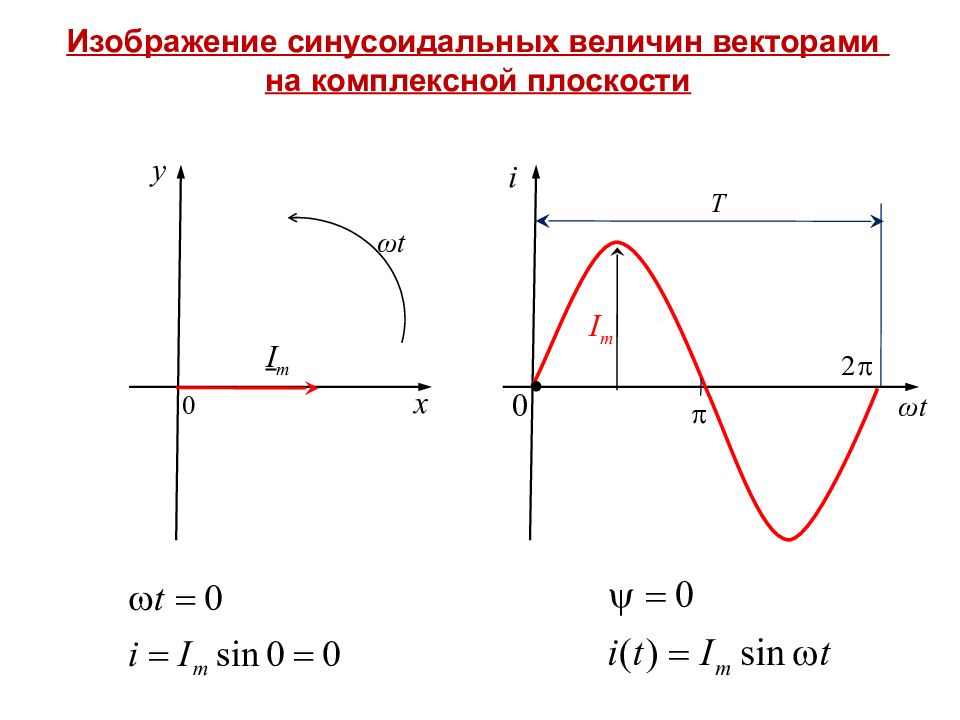
ПЛАН 1. Основные понятия. 2. Геометрическое изображение комплексных чисел. 3. Формы записи комплексных чисел. 4. Действия над комплексными числами. 5. Зачем изучать комплексные числа ?
М x y
На множестве С вводятся понятия функции, предела таким образом, что соответствующие понятия действительного анализа рассматриваются как частный случай. При этом сохраняются известные свойства функций действительного переменного: теоремы о пределах, правила дифференцирования, формулы интегрирования и т.д. Однако, благодаря расширению класса функций появляются новые свойства. Например, доказывается, что из существования производной функции следует существование её производных n -го порядка в области. Устанавливается, что все элементарные функции связаны между собой: тригонометрические функции выражаются через показательную функцию, а обратные тригонометрические функции – через логарифмическую. Значительно глубже, чем в анализе функций действительного переменного, развита геометрическая теория – конформные отображения. Благодаря сочетанию аналитических и геометрических методов теория функций комплексного переменного находит широкое применение в других разделах математики и прикладных задач.
Одним из важных приложений ТФКП является операционное исчисление, которое применяется для решения обыкновенных дифференциальных уравнений и разностных уравнений с постоянными коэффициентами.
