Общая схема исследования функции и построения графика Наибольшее и наименьшее значение функции на отрезке 1
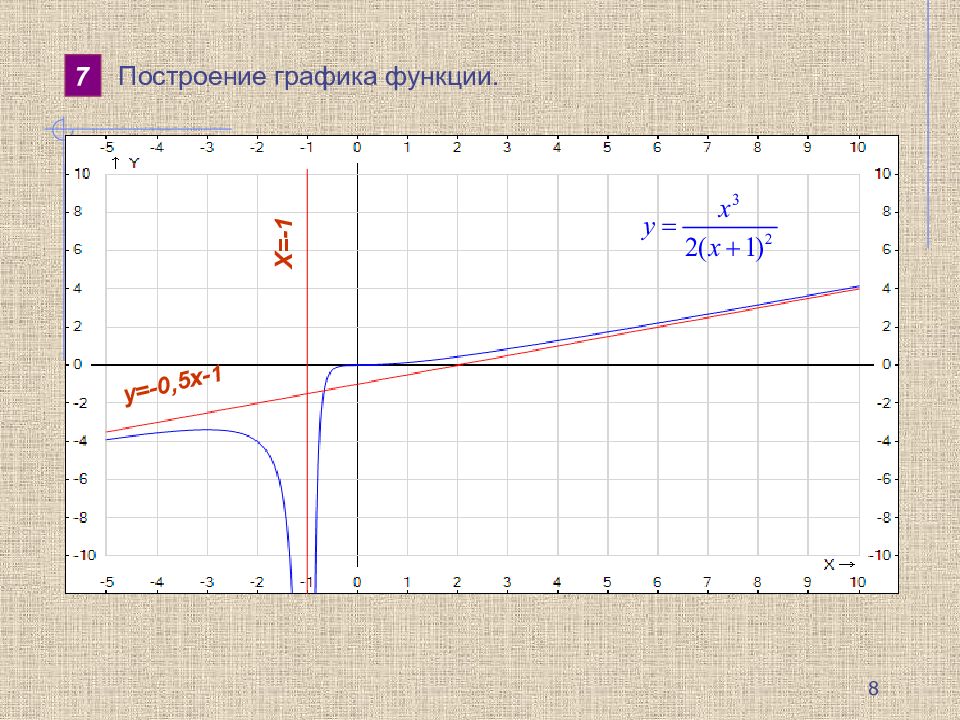
1 Нахождение области определения функции f(x) ; 2 Исследование функции на четность, нечетность 3 Исследование функции на монотонность и экстремум с помощью первой производной; 4 Нахождение асимптот графика функции; Исследование функции на выпуклость и точки перегиба с помощью второй производной; 5 6 Нахождение дополнительных точек (например нахождение точек пересечения графика с осями координат, если это возможно); 7 Построение графика функции. 2
3 1 Область определения: 2 Четность, нечетность функции: функция ни четная ни нечетная
4 3 Монотонность, точки экстремума: не существ. + + + _ -3 -1 0 Точка максимума - функция возрастает - функция убывает - точка максимума
5 4 Выпуклость, точки перегиба: не существ. _ + _ -1 0 Точка перегиба - функция выпукла - функция вогнута - точка перегиба
6 5 Асимптоты: - вертикальная асимптота Найдем наклонные асимптоты: - наклонная асимптота
7 Дополнительные точки: Точки пересечения с осями координат: С осью Ох: С осью Оу: -точка пересечения с осью Ох -точка пересечения с осью Оу
8 7 Построение графика функции. X=-1 y=-0,5x-1
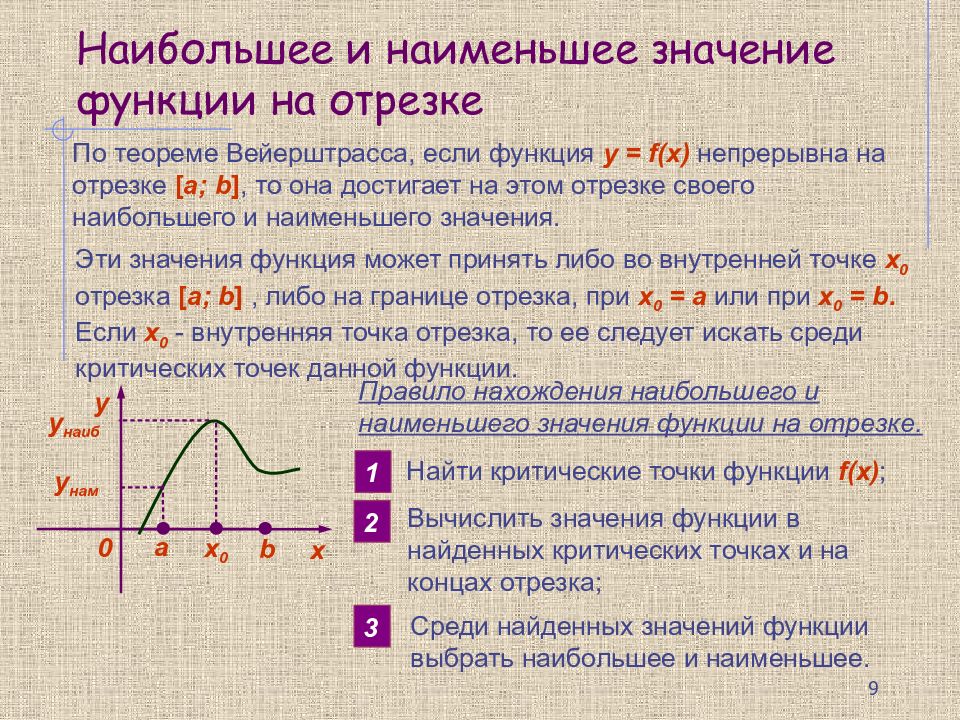
По теореме Вейерштрасса, если функция y = f( х ) непрерывна на отрезке [ a; b ], то она достигает на этом отрезке своего наибольшего и наименьшего значения. Эти значения функция может принять либо во внутренней точке х 0 отрезка [ a; b ], либо на границе отрезка, при х 0 = а или при х 0 = b. Если х 0 - внутренняя точка отрезка, то ее следует искать среди критических точек данной функции. y 0 х a b х 0 у наиб у нам Правило нахождения наибольшего и наименьшего значения функции на отрезке. 1 Найти критические точки функции f(x) ; 2 Вычислить значения функции в найденных критических точках и на концах отрезка; 3 Среди найденных значений функции выбрать наибольшее и наименьшее. 9
10 Совокупная выручка Требуется найти наибольшее значение этой функции на отрезке [1;9]. Найдем критические точки: Вычислим значение функции совокупной выручки на концах интервала и в критической точке: Следовательно, максимальная совокупная выручка составит 4 тыс. руб. при цене за порцию 4 руб. Наибольшее значение.
