Первый слайд презентации: Определение числовой функции и способы её задания
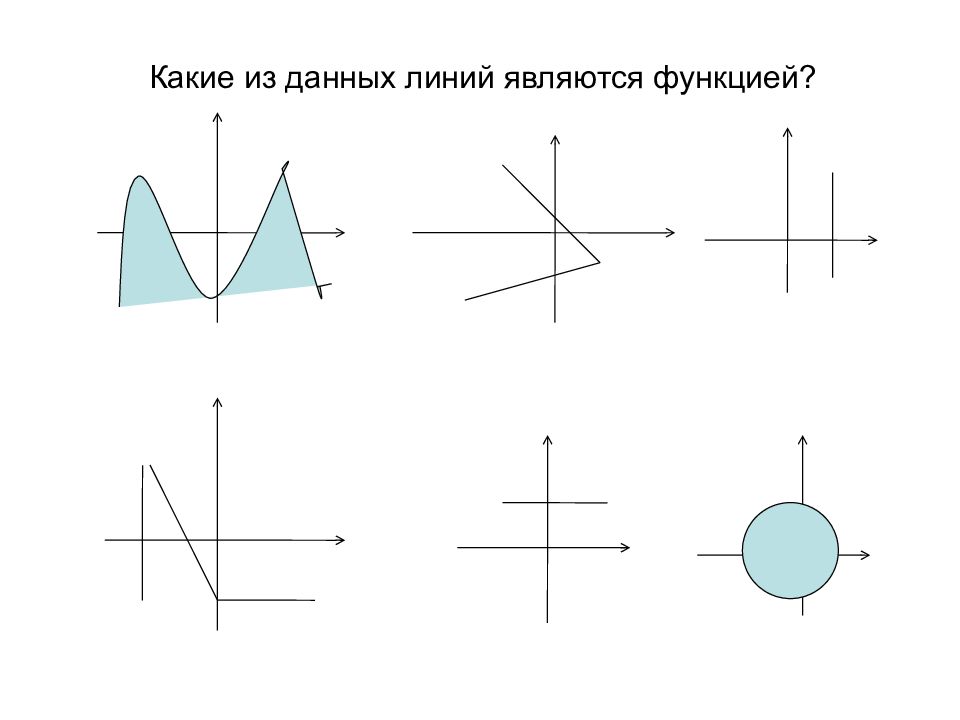
Слайд 2: Что такое функция
Определение. Соответствия, при которых каждому элементу одного множества сопоставляется единственный элемент другого множества называются функциями. Пишут: у = f(x), x Є X. Переменную х называют независимой переменной или аргументом. Множество всех допустимых значений независимой переменной является областью определения функции и обозначается D(y). Переменную у – зависимой переменной. Множество всех значений зависимой переменной является областью значений функции и обозначается Е(у ).
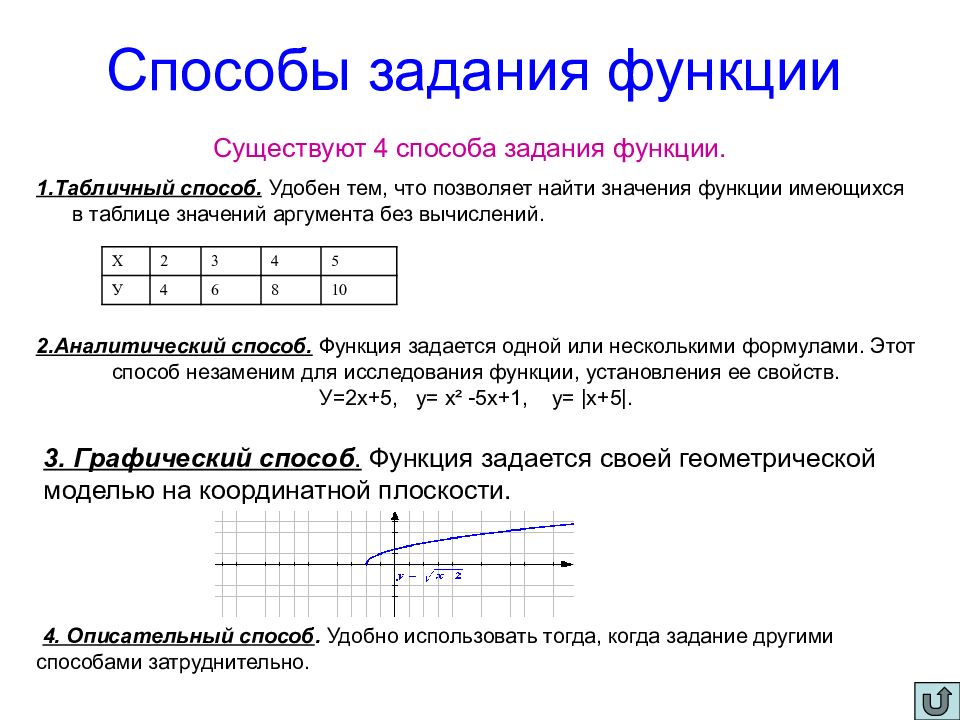
Слайд 3: Способы задания функции
Существуют 4 способа задания функции. 1.Табличный способ. Удобен тем, что позволяет найти значения функции имеющихся в таблице значений аргумента без вычислений. Х 2 3 4 5 У 4 6 8 10 2.Аналитический способ. Функция задается одной или несколькими формулами. Этот способ незаменим для исследования функции, установления ее свойств. У=2х+5, у= х² -5х+1, у= |х+5|. 3. Графический способ. Функция задается своей геометрической моделью на координатной плоскости. 4. Описательный способ. Удобно использовать тогда, когда задание другими способами затруднительно.
Слайд 4: 3
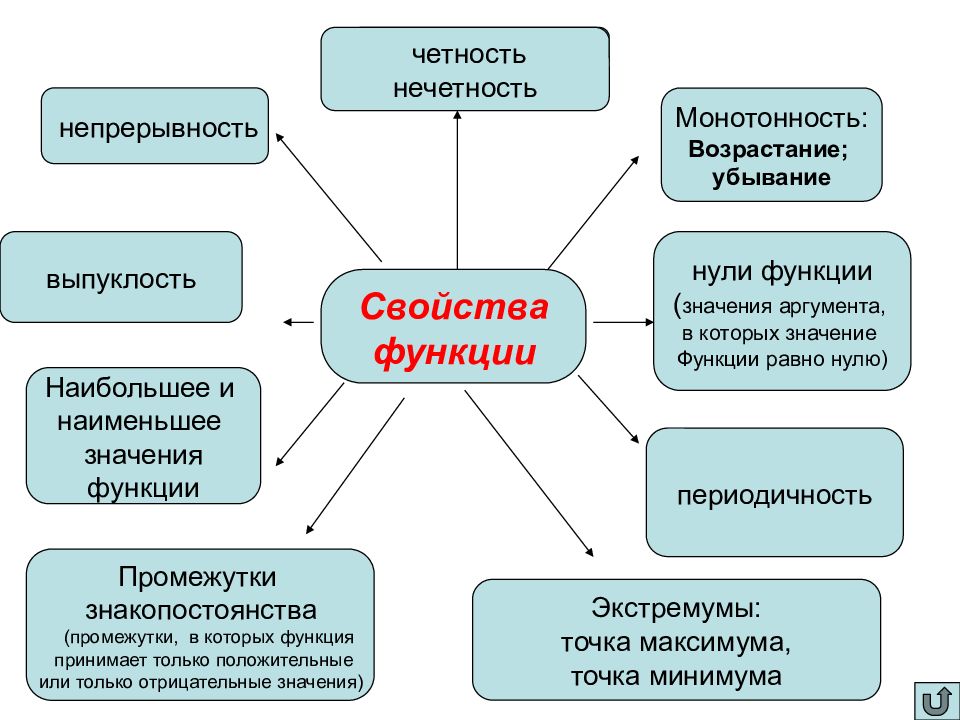
Свойства функции Монотонность: Возрастание; убывание нули функции ( значения аргумента, в которых значение Функции равно нулю) непрерывность периодичность четность нечетность Экстремумы: точка максимума, точка минимума выпуклость Наибольшее и наименьшее значения функции Промежутки знакопостоянства (промежутки, в которых функция принимает только положительные или только отрицательные значения)
Слайд 5: Линейная функция
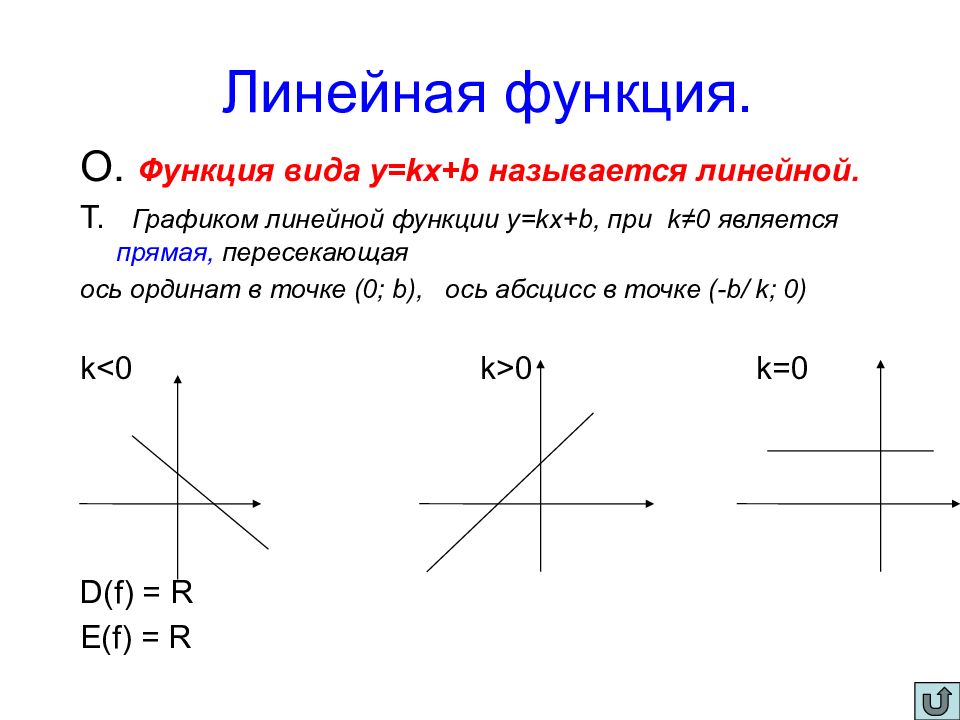
О. Функция вида y=kx+b называется линейной. Т. Графиком линейной функции y=kx+b, при k ≠ 0 является прямая, пересекающая ось ординат в точке (0; b ), ось абсцисс в точке (- b / k ; 0) k < 0 k > 0 k =0 D(f) = R E(f) = R
Слайд 6
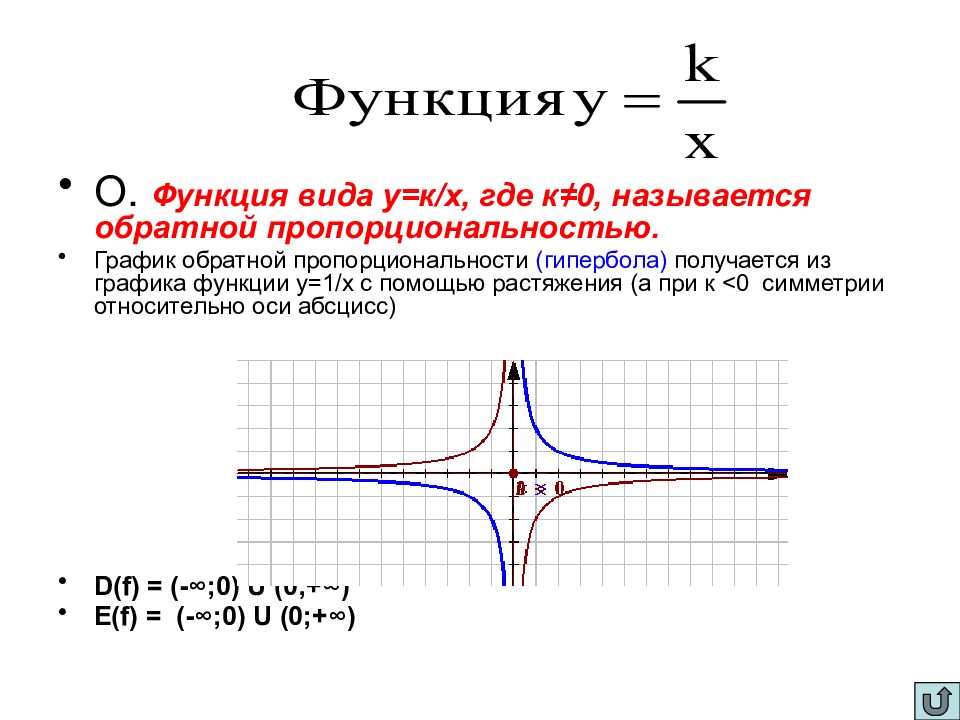
О. Функция вида у=к/х, где к ≠0, называется обратной пропорциональностью. График обратной пропорциональности (гипербола) получается из графика функции у=1/х с помощью растяжения (а при к < 0 симметрии относительно оси абсцисс) D(f) = (-∞;0) U (0;+∞) E(f) = (-∞;0) U (0;+∞)
Слайд 7: Степенная функция с целым показателем
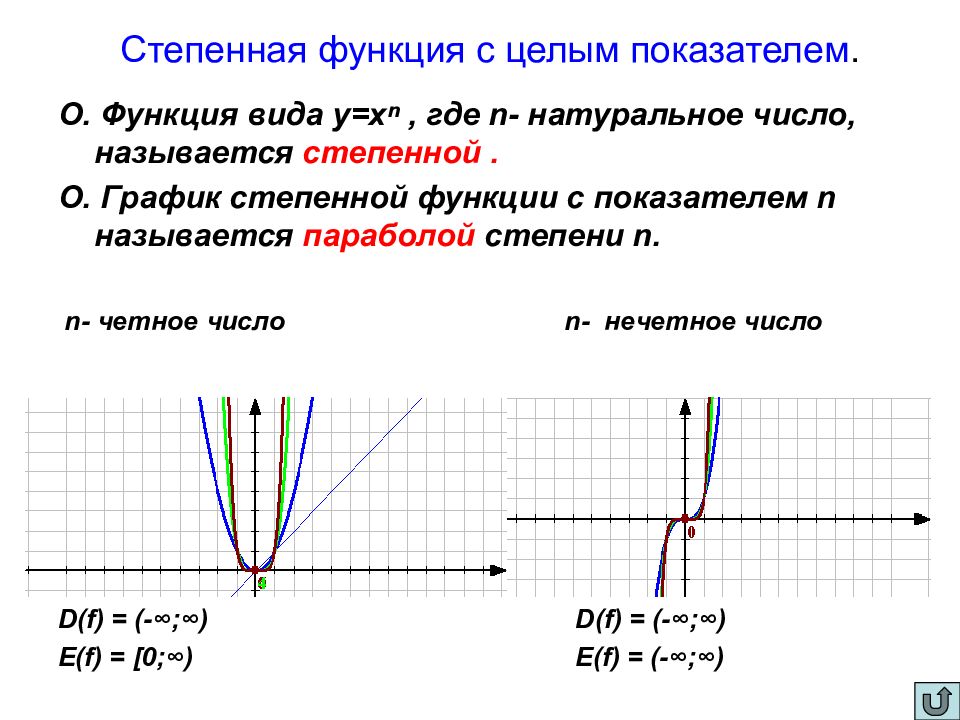
О. Функция вида у=х ⁿ, где n - натуральное число, называется степенной. О. График степенной функции с показателем n называется параболой степени n. n - четное число n - нечетное число D(f) = (-∞;∞) D(f) = (-∞;∞) E(f) = [0;∞) E(f) = (-∞;∞)
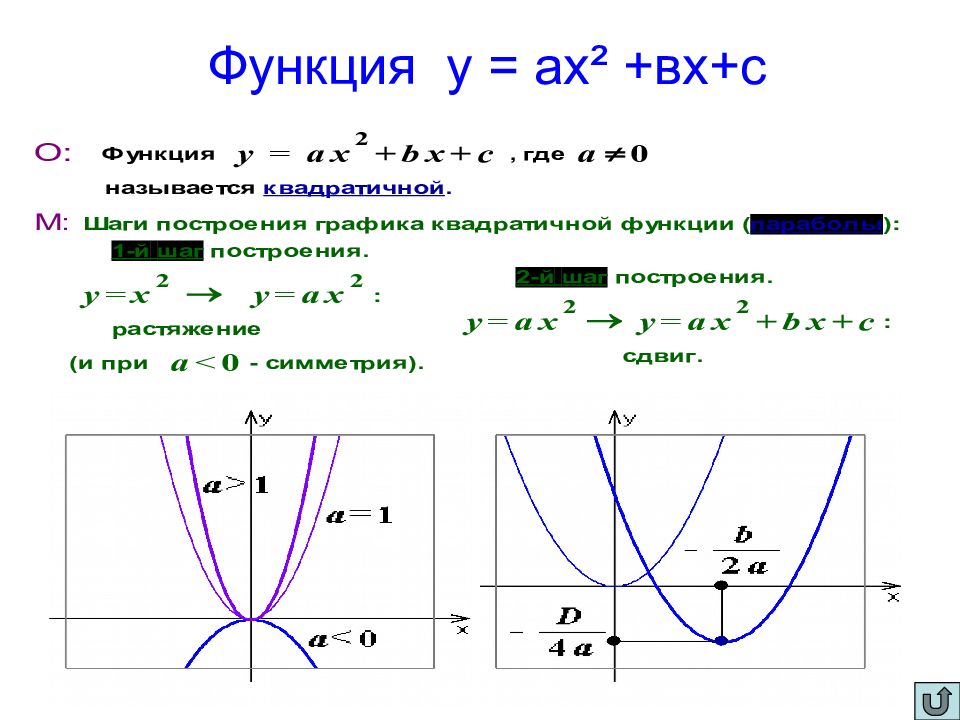
Слайд 8: Функция у = ах ² +вх+с
Слайд 9
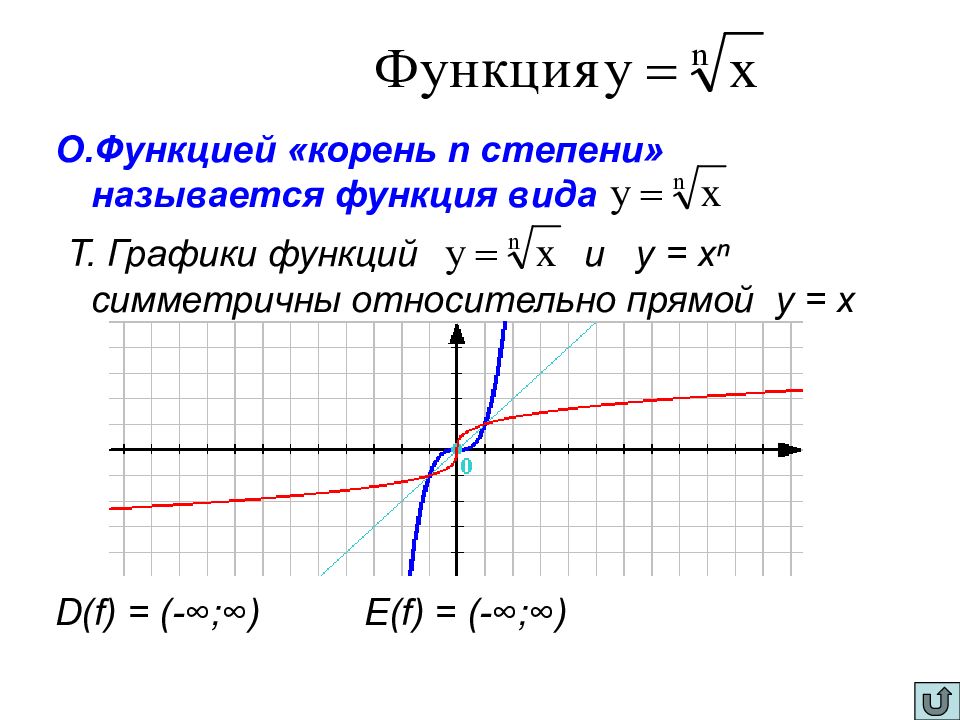
О.Функцией «корень n степени» называется функция вида Т. Графики функций и у = хⁿ симметричны относительно прямой у = х D(f) = (-∞;∞) E(f) = (-∞;∞)
Слайд 10: Функция у = | х |
у= | х | = х, если х≥0 -х, если х < 0 Функция задается кусочно. х < 0 х ≥0 Т. Область определения функции D( y)= (-∞ ; + ∞ ) Множество значений функции Е(у)= [ 0; + ∞ ) Т. Функция у = | х | убывает при х Є (-∞ ; 0 ] возрастает при х Є [ 0; + ∞ )
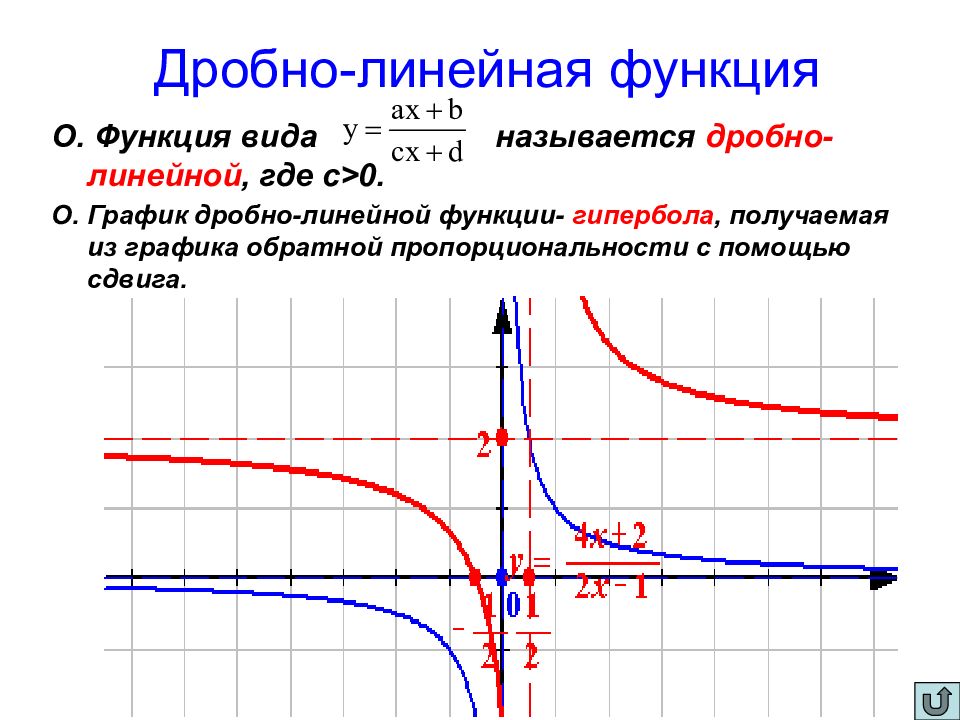
Слайд 11: Дробно-линейная функция
О. Функция вида называется дробно-линейной, где с > 0. О. График дробно-линейной функции- гипербола, получаемая из графика обратной пропорциональности с помощью сдвига.
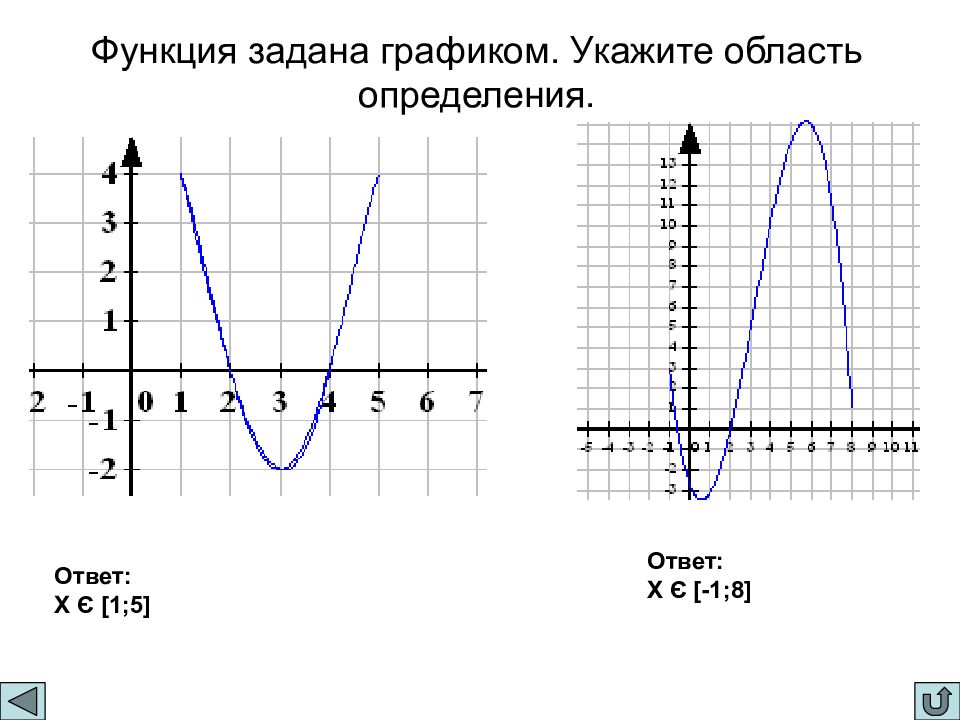
Слайд 13: Функция задана графиком. Укажите область определения
Ответ: X Є [ 1;5 ] Ответ: X Є [ -1;8 ]
Слайд 14: Множество значений функции
у= 2sin ²x-cos2x Решение: 2sin ²x-cos2x = 2sin²x-(1-2sin²x)=4sin²x-1 0 ≤ Sin²x ≤ 1, -1 ≤ 4sin²x-1 ≤ 3 Ответ: -1 ≤ у ≤ 3 у = 1 - 2 |cosx| Решение: -1 ≤ cosx ≤ 1, 0 ≤ |cosx| ≤ 1, -1 ≤ 1 - 2 |cosx| ≤ 1 ≤ 1 Ответ: -1 ≤ у ≤ 1 3.Функция задана графиком. Укажите множество значений этой функции. E(f)=(-2;2] E(f)= [-3;1] E(f)= (-∞;4]
Слайд 15: Решение неравенств
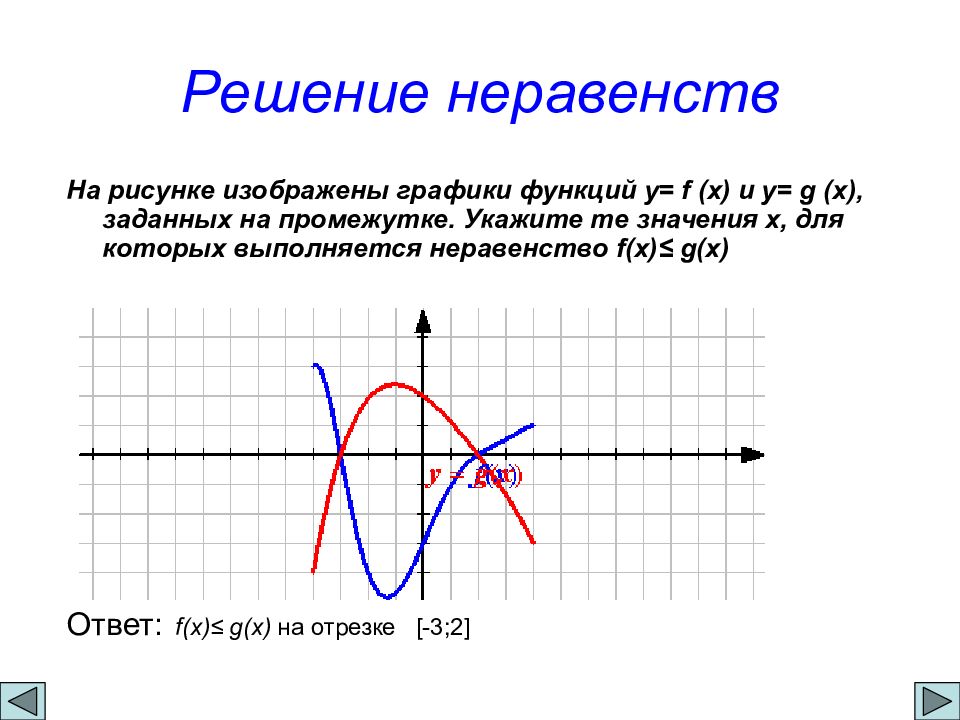
На рисунке изображены графики функций y= f (x) и y= g (x), заданных на промежутке. Укажите те значения х, для которых выполняется неравенство f(x) ≤ g(x) Ответ: f(x) ≤ g(x) на отрезке [ -3;2 ]
Слайд 16: На рисунке изображен график функции у = f(x), заданной на отрезке [ -4;7 ]. Укажите те значения х, для которых выполняется неравенство f(x)≤-2
Ответ: [ 0; 2 ]





![Определение числовой функции и способы её задания На рисунке изображен график функции у = f(x), заданной на отрезке [ -4;7 ]. Укажите те значения х, для которых выполняется неравенство f(x)≤-2](https://s1.showslide.ru/s_slide/a61a054156e45c55c33e458542c1c86d/355b96c6-5673-41df-aabb-fcbe8a3c2cfe.jpeg)