Автор: доцент кафедры информатики и математики Грязнов Сергей Александрович ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА
Предположим, что варианты выборки расположены в возрастающем порядке, т.е. в виде вариационного ряда.
Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.
Условными называют варианты, определяемые равенством : где С —ложный нуль (новое начало отсчета); h —шаг, т.е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).
Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными.
В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).
Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.
Найти условные варианты статистического распределения:
Выберем в качестве ложного нуля варианту 33,6 (эта варианта расположена в середине вариационного ряда). Найдем шаг:
Найдем условную варианту: Аналогично получим: и 2 = - 1, и 3 = 0, и 4 =1, и 5 =2. Мы видим, что условные варианты – небольшие целые числа. Разумеется, оперировать с ними проще, чем с первоначальными вариантами.
Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами. В отличии от теоретических эмпирические вычисляют по данным наблюдений.
Обычным эмпирическим моментом порядка k называют среднее значение k - x степеней разностей x i — С:
Начальным эмпирическим моментом порядка k называют обычный момент порядка k при С = 0
В частности, т.е. начальный эмпирический момент первого порядка равен выборочной средней.
Центральным эмпирическим моментом порядка k называют обычный момент порядка k при
В частности, т.е. центральный эмпирический момент второго порядка равен выборочной дисперсии.
Легко выразить центральные моменты через обычные :
Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчеты, заменяют первоначальные варианты условными.
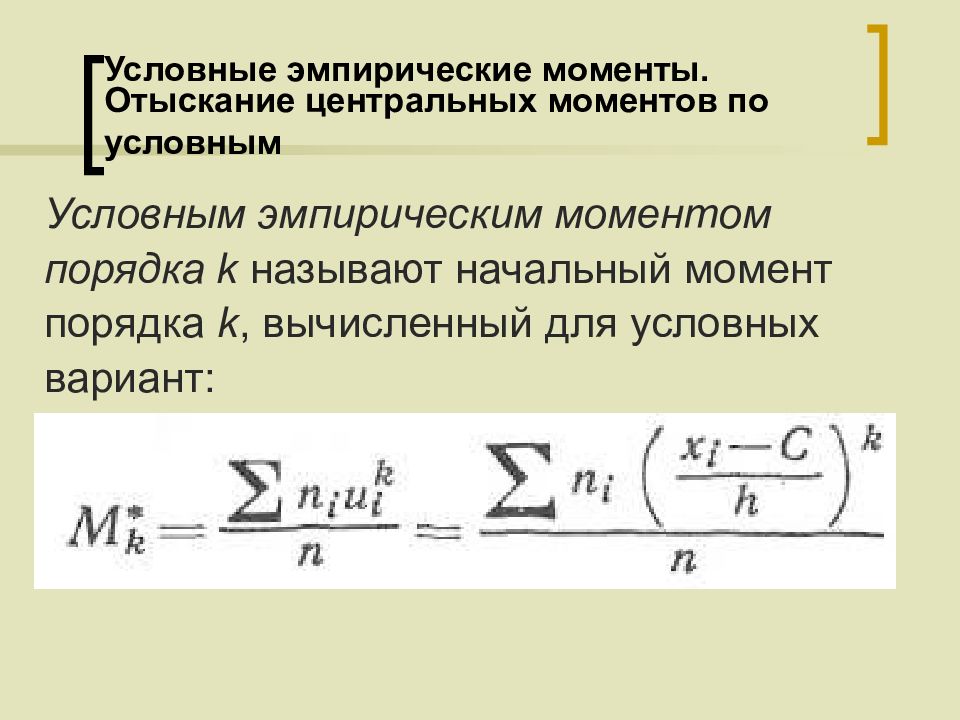
Условным эмпирическим моментом порядка k называют начальный момент порядка k, вычисленный для условных вариант:
В частности,
Отсюда, Таким образом, для того чтобы найти выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на h и к результату прибавить ложный нуль С.
Выразим обычные моменты через условные:
Отсюда, Таким образом, для того чтобы найти обычный момент порядка k, достаточно условный момент того же порядка умножить на h k.
Найдя же обычные моменты, легко найти цент- ральные моменты. В итоге получим удобные для вычислений формулы, выражающие цент- ральные моменты через условные:
В частности, получим формулу для вычисления выборочной дисперсии по условным моментам первого и второго порядков
Метод произведений дает удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная же условные моменты, нетрудно найти интересующие нас начальные и центральные эмпирические моменты.
В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется по следующим правилам:
1) в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;
2) во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n ) помещают в нижнюю клетку столбца;
3) в третий столбец записывают условные варианты u i = ( x i — C )/ h, причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над нулем пишут последовательно —1, —2, —3 и т.д., а под нулем — 1, 2, 3 и т.д.;
4) умножают частоты на условные варианты и записывают их произведения n i u i в четвертый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца;
5) умножают частоты на квадраты условных вариант и записывают их произведения n i u i 2 в пятый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца;
6) умножают частоты на квадраты условных вариант, увеличенных каждая на единицу, и записывают произведения в шестой контрольный столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца.
Целесообразно отдельно складывать отрицательные числа четвертого столбца (их сумму А 1 записывают в клетку строки, содержащей ложный нуль) и отдельно положительные числа (их сумму А 2 записывают в предпоследнюю клетку столбца); тогда
При вычислении произведений n i u i 2 пятого столбца целесообразно числа n i u i четвертого столбца умножать на u i.
После того как расчетная таблица заполнена и проверена правильность вычислений, вычисляют условные моменты:
Наконец, вычисляют выборочные среднюю и дисперсию:
Найти методом произведений выборочные среднюю и дисперсию следующего статистического распределения:
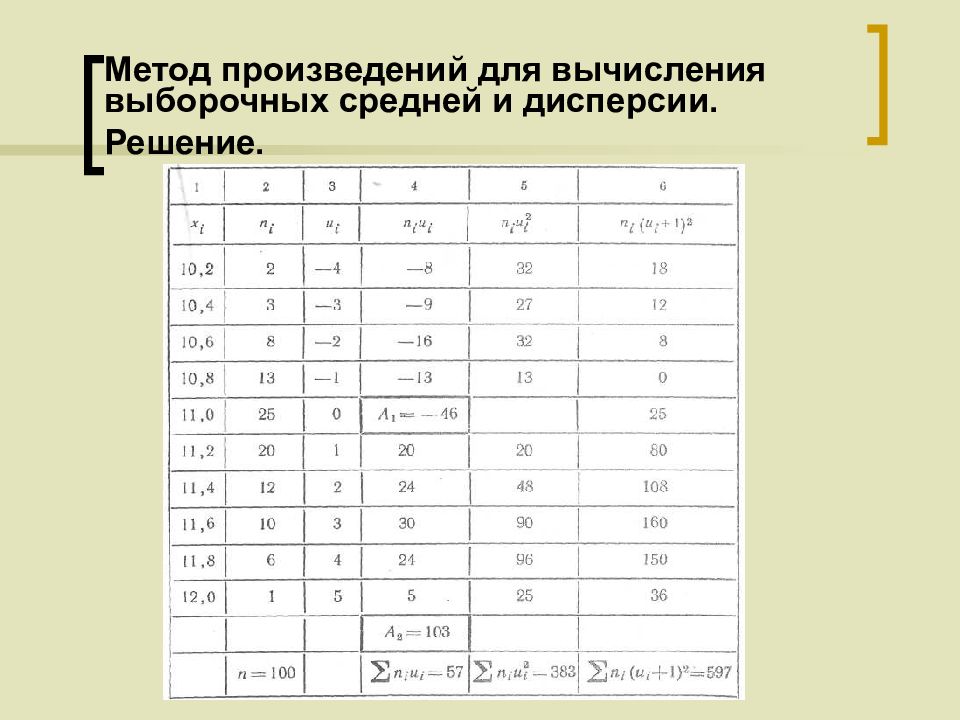
Составим расчетную таблицу, для чего: 1) запишем варианты в первый столбец; 2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца;
3) в качестве ложного нуля выберем варианту 11,0 (эта варианта расположена примерно в середине вариационного ряда); в клетке третьего столбца, которая принадлежит строке, содержащей выбранный ложный нуль, пишем 0; над нулем записываем последовательно —1, —2, —3, —4, а под нулем — 1, 2, 3, 4, 5;
4) произведения частот на условные варианты записываем в четвертый столбец; отдельно находим сумму (—46) отрицательных и отдельно сумму (103) положительных чисел; сложив эти числа, их сумму (57) помещаем в нижнюю клетку столбца;
5) произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (383) помещаем в нижнюю клетку столбца;
6) произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой контрольный столбец; сумму (597) чисел столбца помещаем в нижнюю клетку столбца.
Вычислим условные моменты первого и второго порядков:
Найдем шаг: Вычислим искомые выборочные среднюю и дисперсию:
Автор: доцент кафедры информатики и математики Грязнов Сергей Александрович ВЫСШАЯ ШКОЛА ПРИВАТИЗАЦИИ И ПРЕДПРИНИМАТЕЛЬСТВА
