Первый слайд презентации: Метод параллельного проектирования. Изображение пространственных фигур на плоскости
Воробьев Леонид Альбертович, г.Минск
Для решения этой задачи применяется метод параллельного проектирования. Выясним его суть на примере простейшей геометрической фигуры – точки. Итак, у нас есть геометрическая фигура в пространстве – точка А. А
Слайд 3
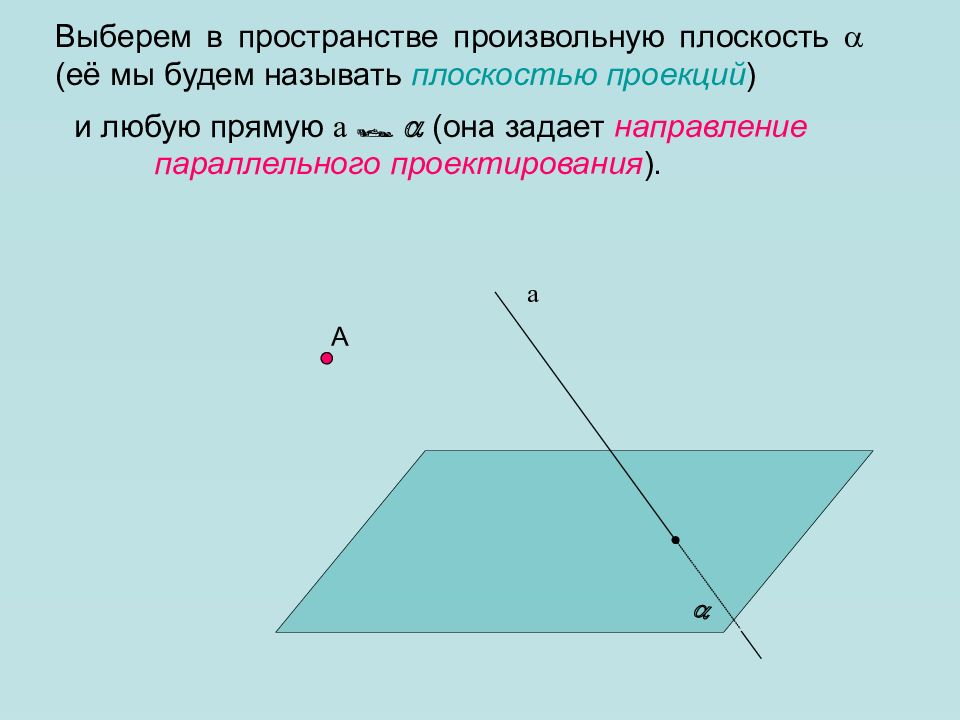
А Выберем в пространстве произвольную плоскость (её мы будем называть плоскостью проекций ) и любую прямую a (она задает направление параллель ного проектирования ). а
Слайд 4
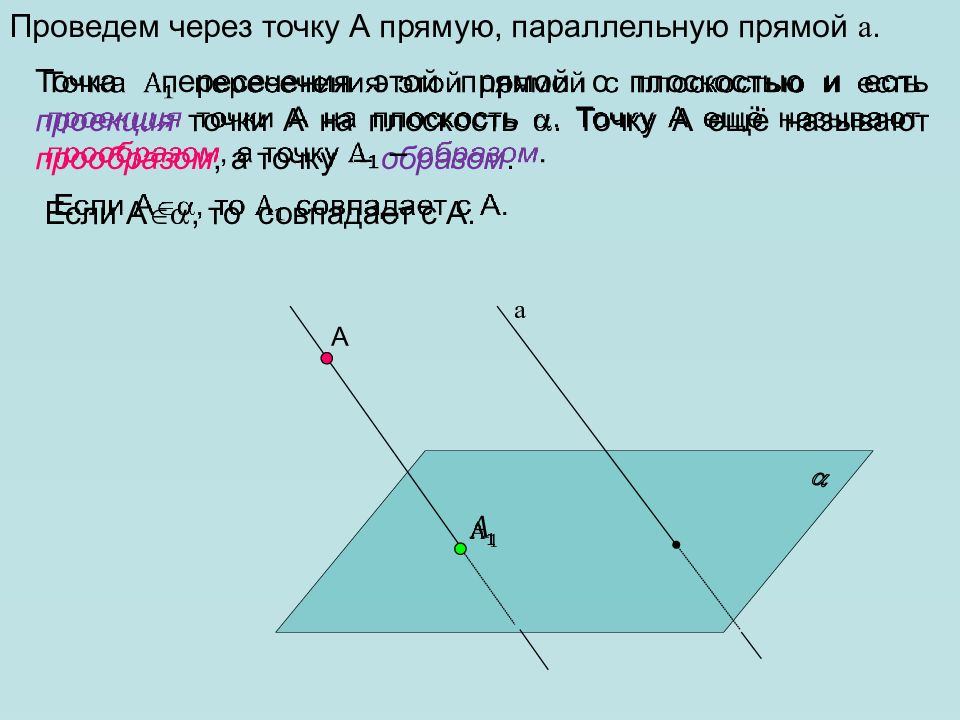
А а Проведем через точку А прямую, параллельную прямой а. Точка пересечения этой прямой с плоскостью и есть проекция точки А на плоскость . Точку А ещё называют прообразом, а точку – образом. Если А , то совпадает с А.
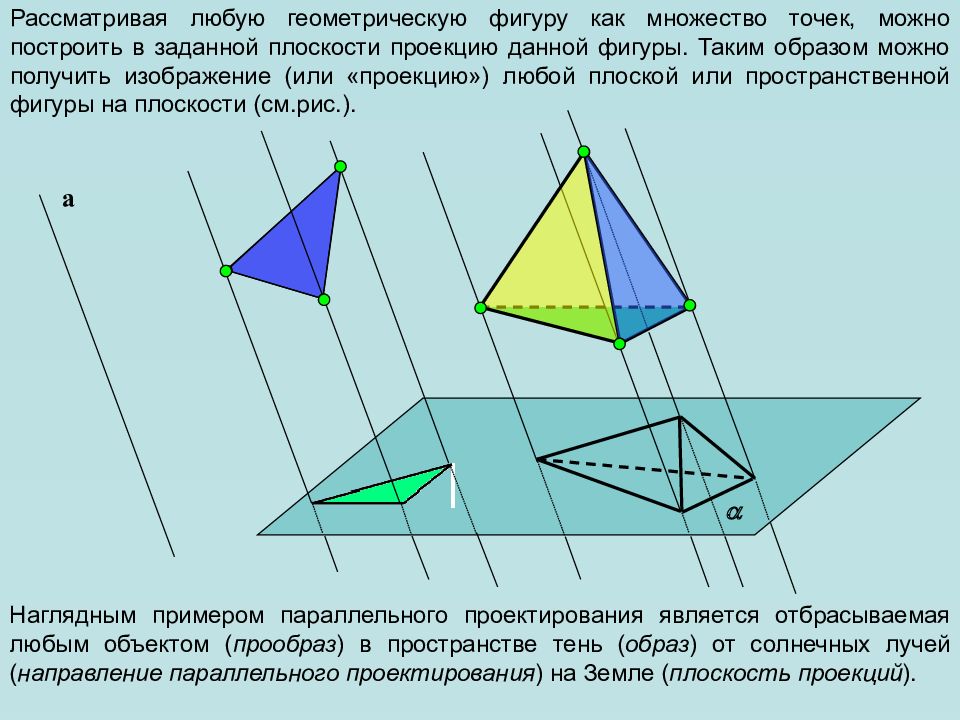
а Наглядным примером параллельного проектирования является отбрасываемая любым объектом ( прообраз ) в пространстве тень ( образ ) от солнечных лучей ( направление параллельного проектирования ) на Земле ( плоскость проекций ).
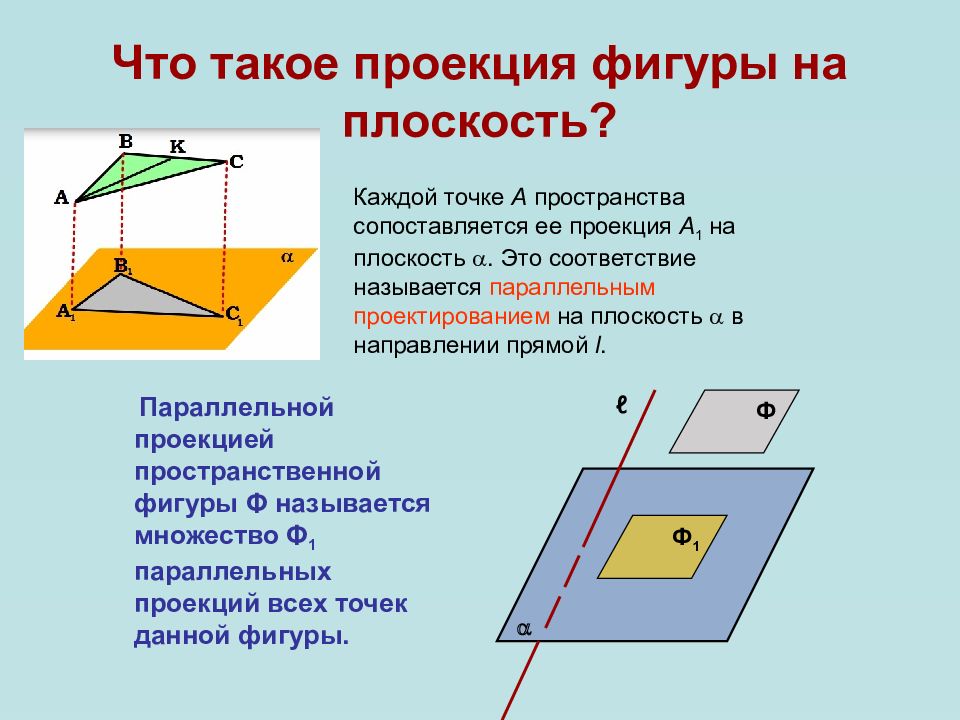
Параллельной проекцией пространственной фигуры Φ называется множество Φ 1 параллельных проекций всех точек данной фигуры. Ф Ф 1 ℓ Каждой точке A пространства сопоставляется ее проекция A 1 на плоскость . Это соответствие называется параллельным проектированием на плоскость в направлении прямой l.
Слайд 7
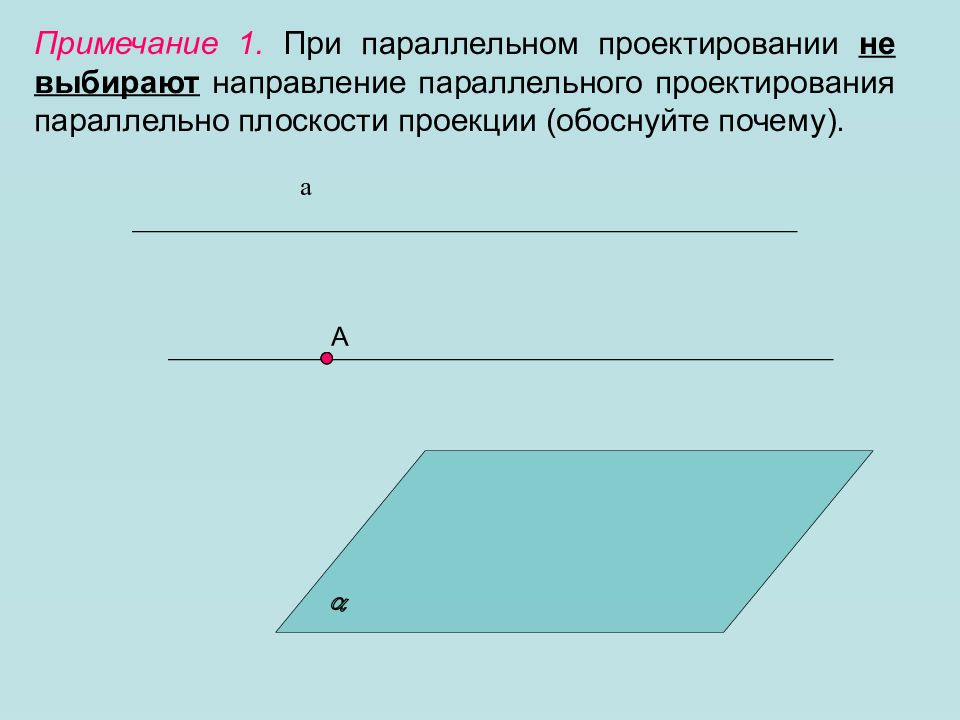
Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции (обоснуйте почему). А а
Слайд 8
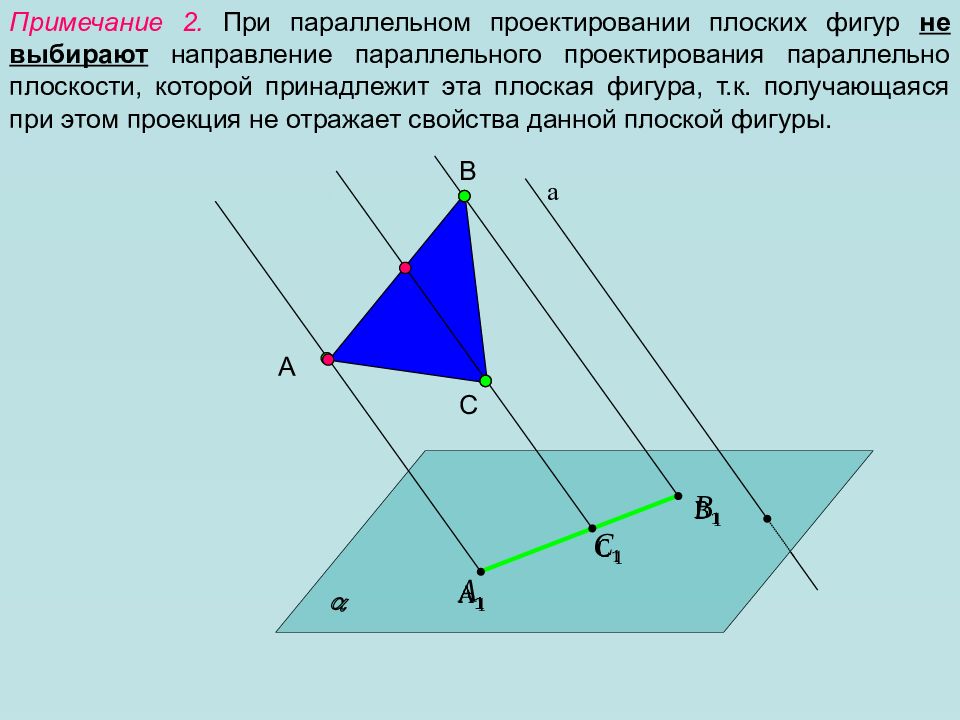
Примечание 2. При параллельном проектировании плоских фигур не выбирают направление параллельного проектирования параллельно плоскости, которой принадлежит эта плоская фигура, т.к. получающаяся при этом проекция не отражает свойства данной плоской фигуры. А а B C
Слайд 9
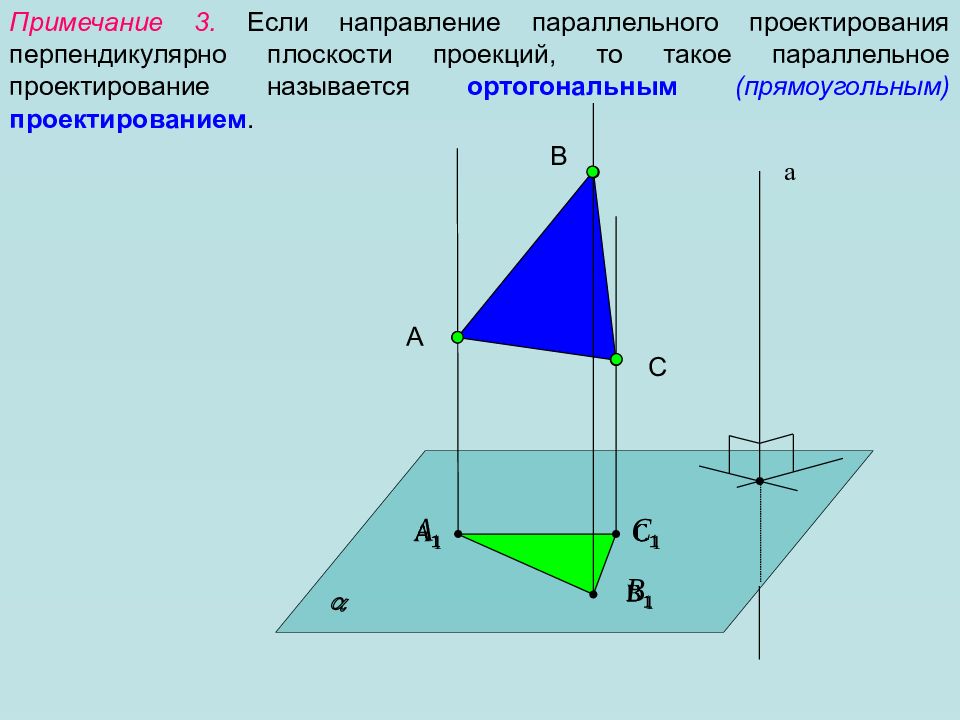
Примечание 3. Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным (прямоугольным) проектированием. А а B C
Слайд 10
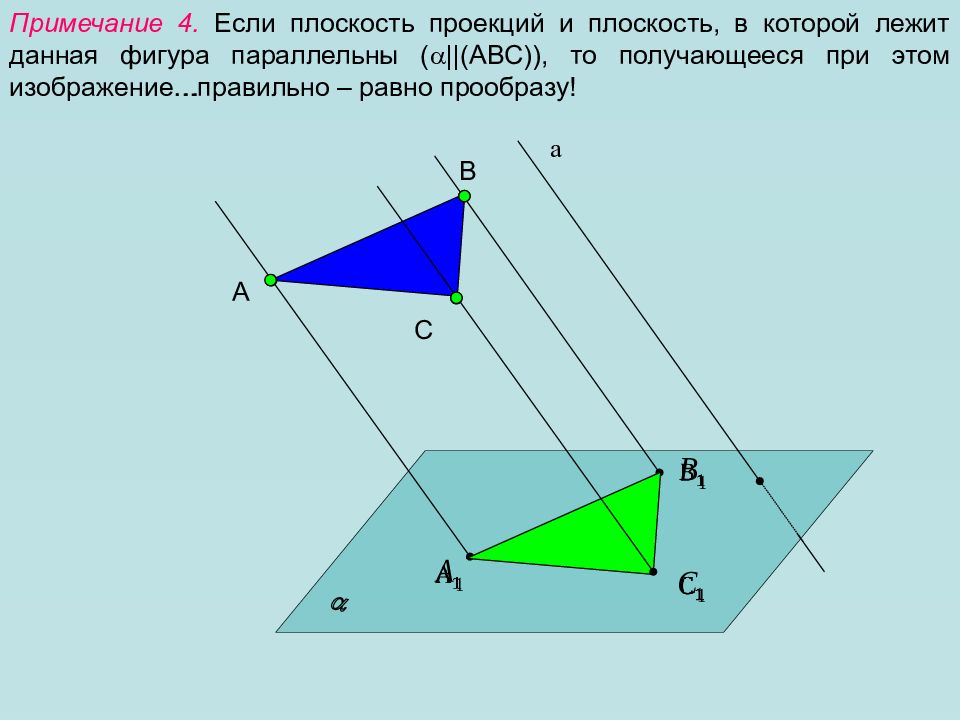
Примечание 4. Если плоскость проекций и плоскость, в которой лежит данная фигура параллельны ( || (АВС)), то получающееся при этом изображение… А а B C … правильно – равно прообразу!
Слайд 11
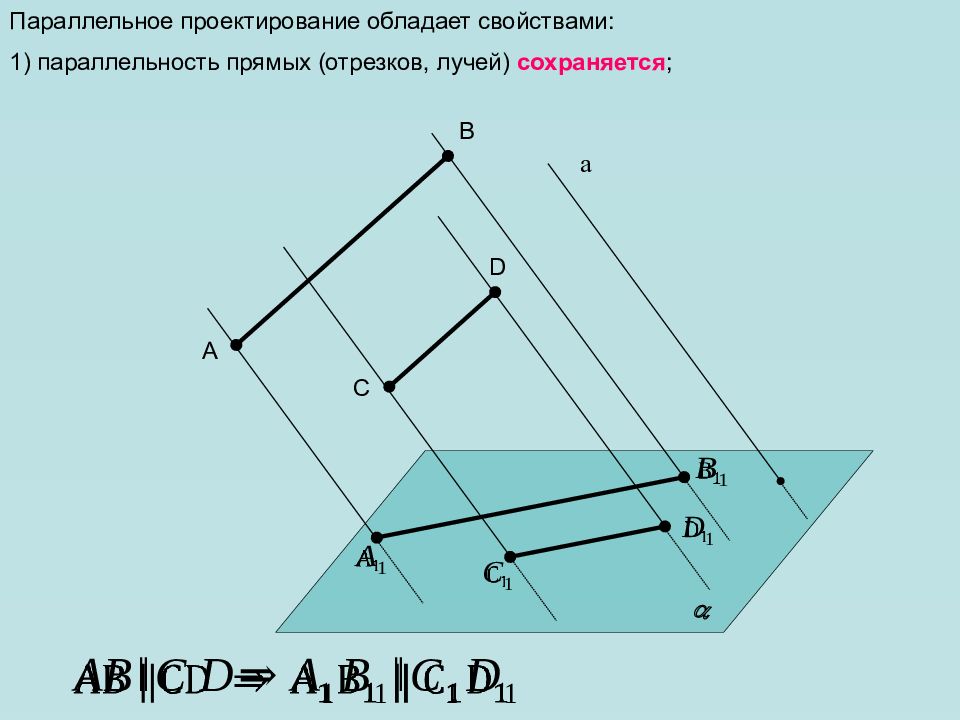
Параллельное проектирование обладает свойствами: 1) параллельность прямых (отрезков, лучей) сохраняется ; а A D C B
Слайд 12
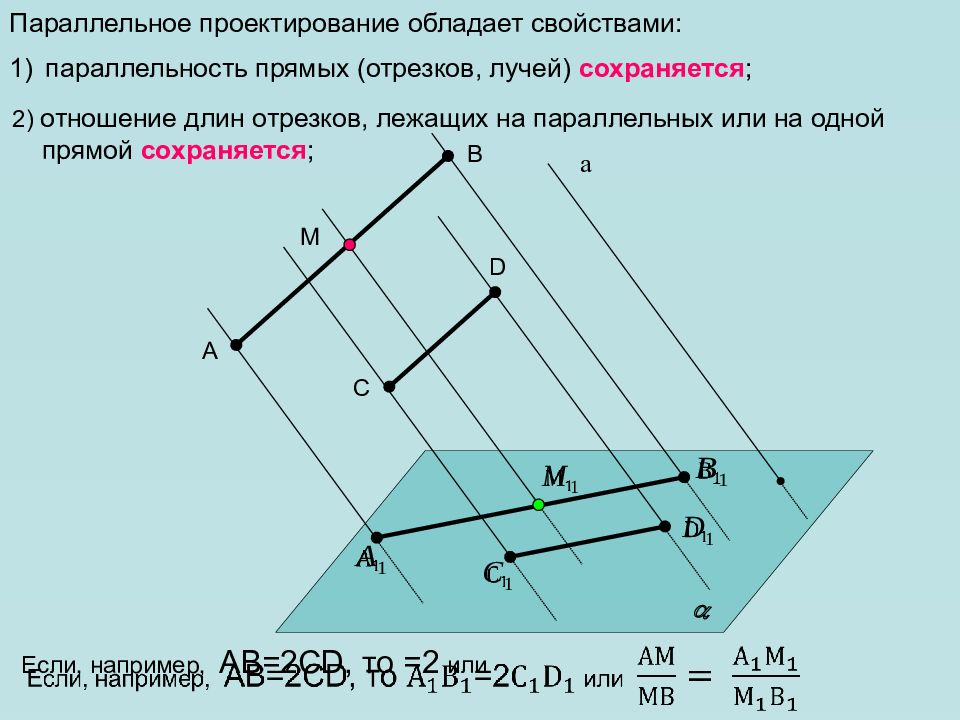
2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется ; Параллельное проектирование обладает свойствами: параллельность прямых (отрезков, лучей) сохраняется ; а A D C B Если, например, АВ=2 CD, то =2 или М
Слайд 13
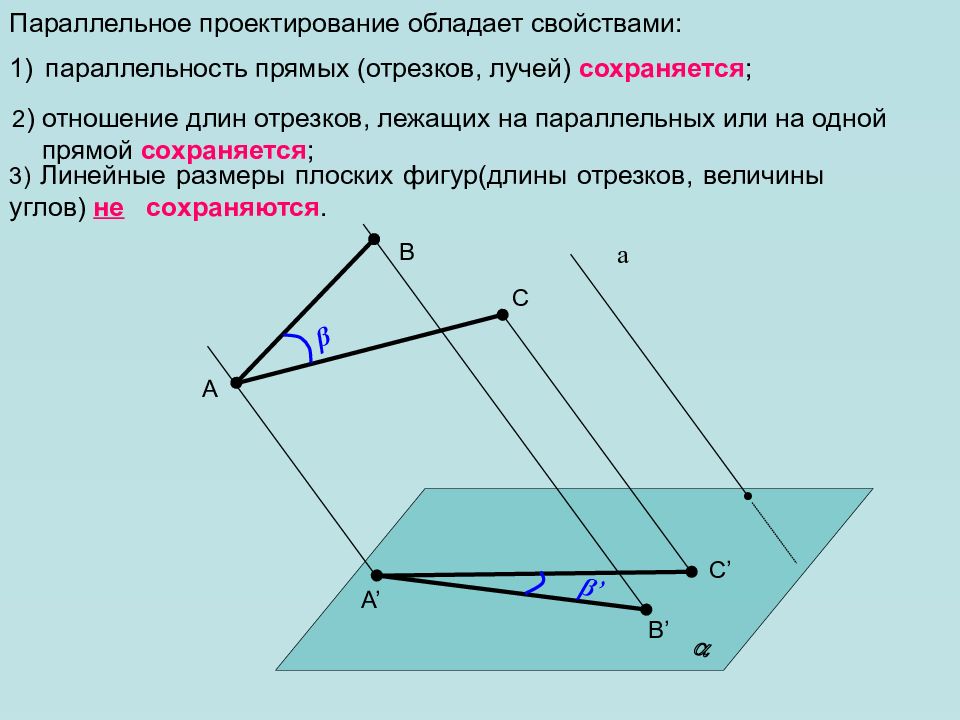
Параллельное проектирование обладает свойствами: параллельность прямых (отрезков, лучей) сохраняется ; а A B A’ B’ 3) Линейные размеры плоских фигур(длины отрезков, величины углов) не сохраняются. 2 ) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется ; β β ’ C C’
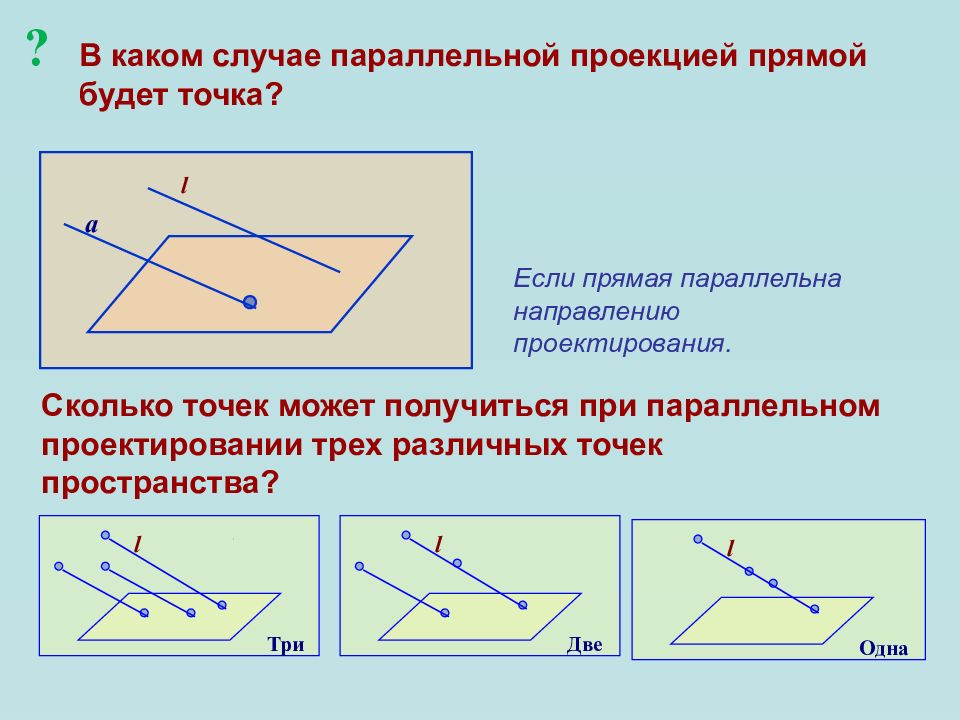
Слайд 14: В каком случае параллельной проекцией прямой будет точка?
l a Если прямая параллельна направлению проектирования. Сколько точек может получиться при параллельном проектировании трех различных точек пространства? l Три l Две l Одна ?
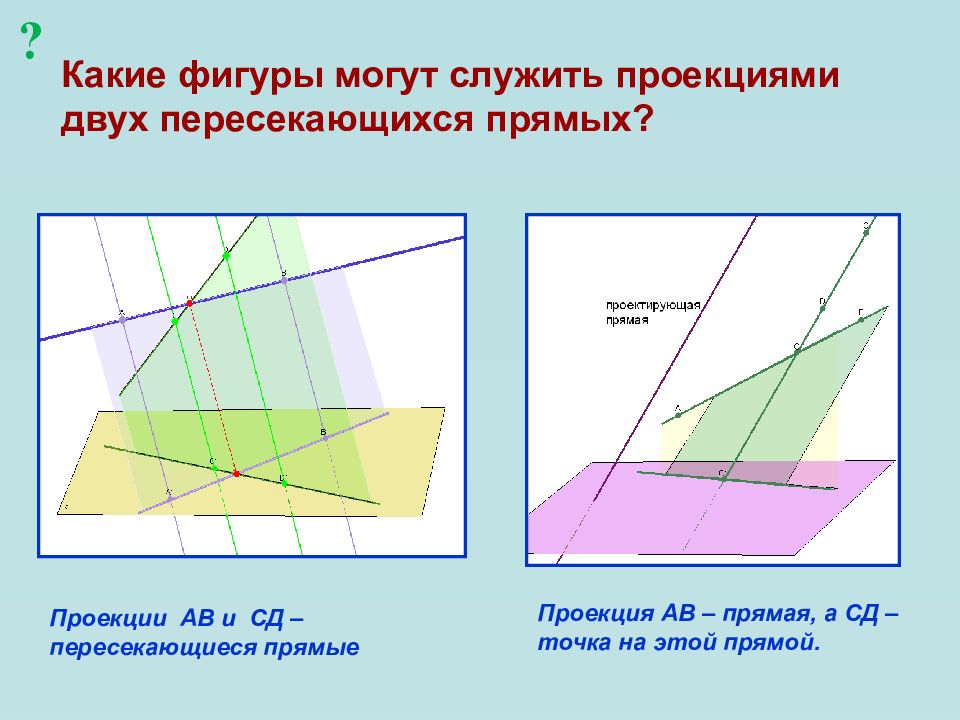
Слайд 15: Какие фигуры могут служить проекциями двух пересекающихся прямых?
? Проекции АВ и СД – пересекающиеся прямые Проекция АВ – прямая, а СД – точка на этой прямой.
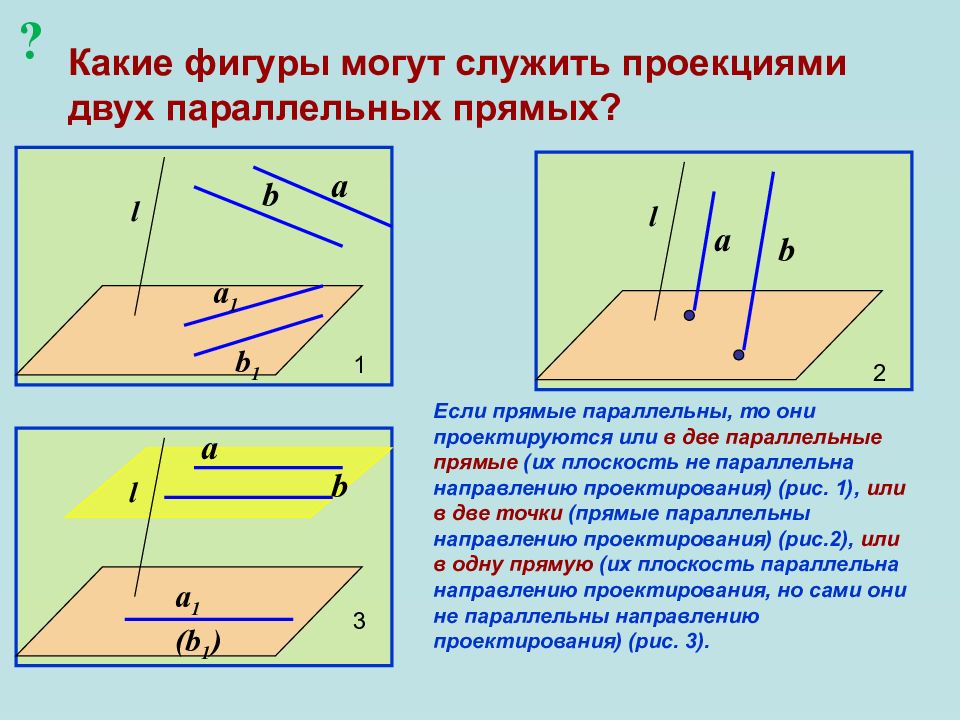
Слайд 16: Какие фигуры могут служить проекциями двух параллельных прямых?
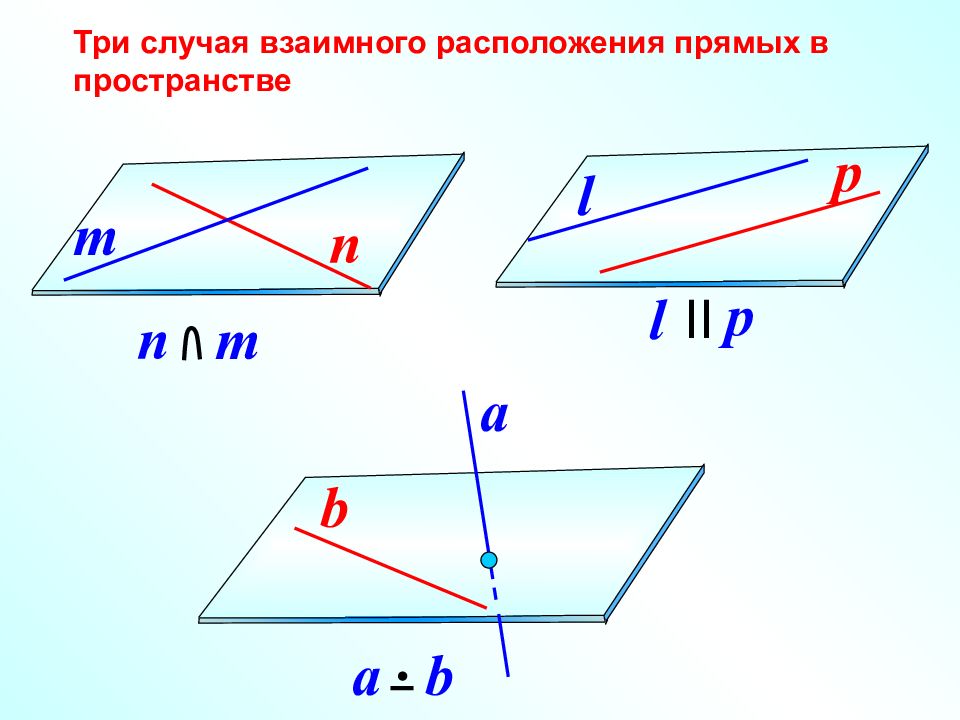
a b b 1 a 1 l a b l a b l a 1 (b 1 ) 1 2 3 Если прямые параллельны, то они проектируются или в две параллельные прямые (их плоскость не параллельна направлению проектирования) (рис. 1), или в две точки (прямые параллельны направлению проектирования) (рис.2), или в одну прямую (их плоскость параллельна направлению проектирования, но сами они не параллельны направлению проектирования) (рис. 3). ?
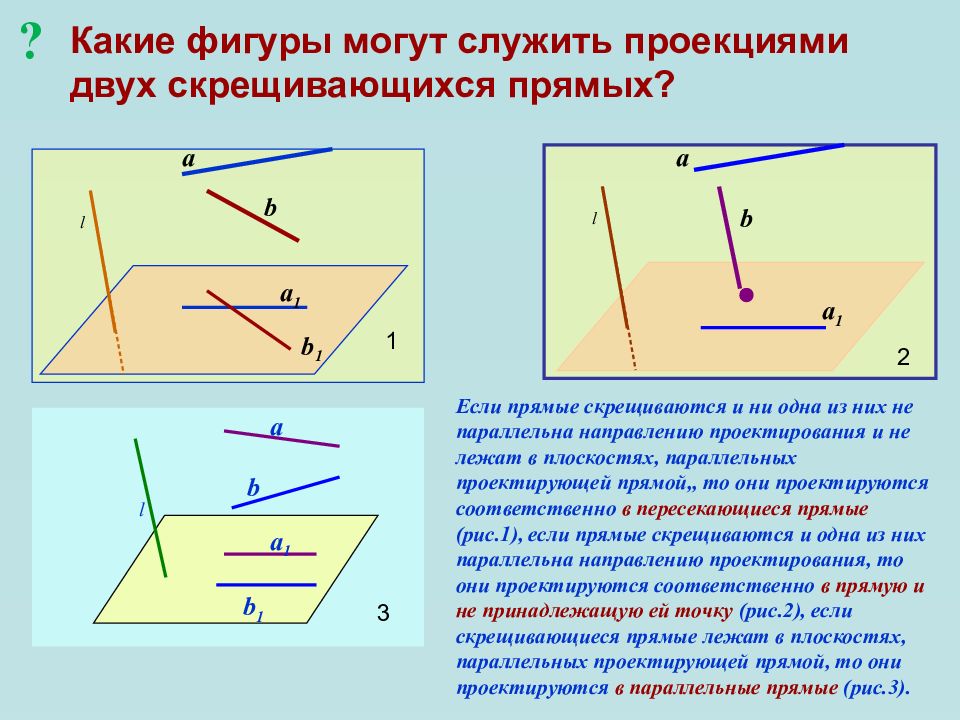
Слайд 17: Какие фигуры могут служить проекциями двух скрещивающихся прямых?
a b a 1 b 1 l a b a 1 l Если прямые скрещиваются и ни одна из них не параллельна направлению проектирования и не лежат в плоскостях, параллельных проектирующей прямой,, то они проектируются соответственно в пересекающиеся прямые (рис.1), если прямые скрещиваются и одна из них параллельна направлению проектирования, то они проектируются соответственно в прямую и не принадлежащую ей точку (рис.2), если скрещивающиеся прямые лежат в плоскостях, параллельных проектирующей прямой, то они проектируются в параллельные прямые (рис.3). 1 2 b a 1 b 1 l a 3 ?
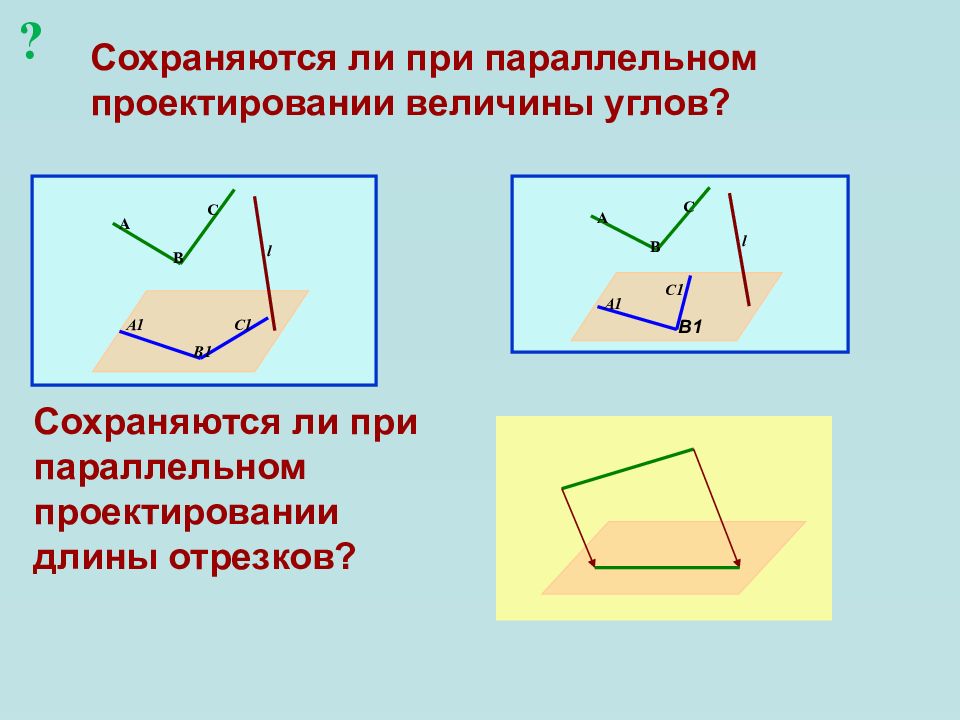
Слайд 18: Сохраняются ли при параллельном проектировании величины углов?
l A B C A1 B1 C1 l A B C A1 C1 Сохраняются ли при параллельном проектировании длины отрезков? B1 ?
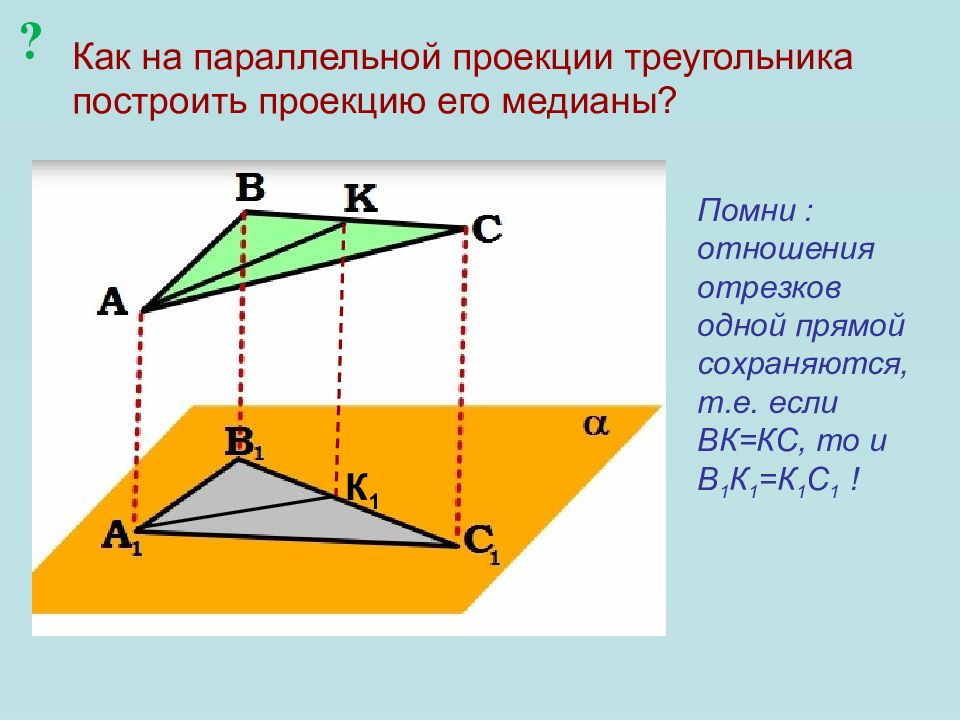
Слайд 19: Как на параллельной проекции треугольника построить проекцию его медианы?
К 1 Помни : отношения отрезков одной прямой сохраняются, т.е. если ВК=КС, то и В 1 К 1 =К 1 С 1 ! ?
Слайд 20
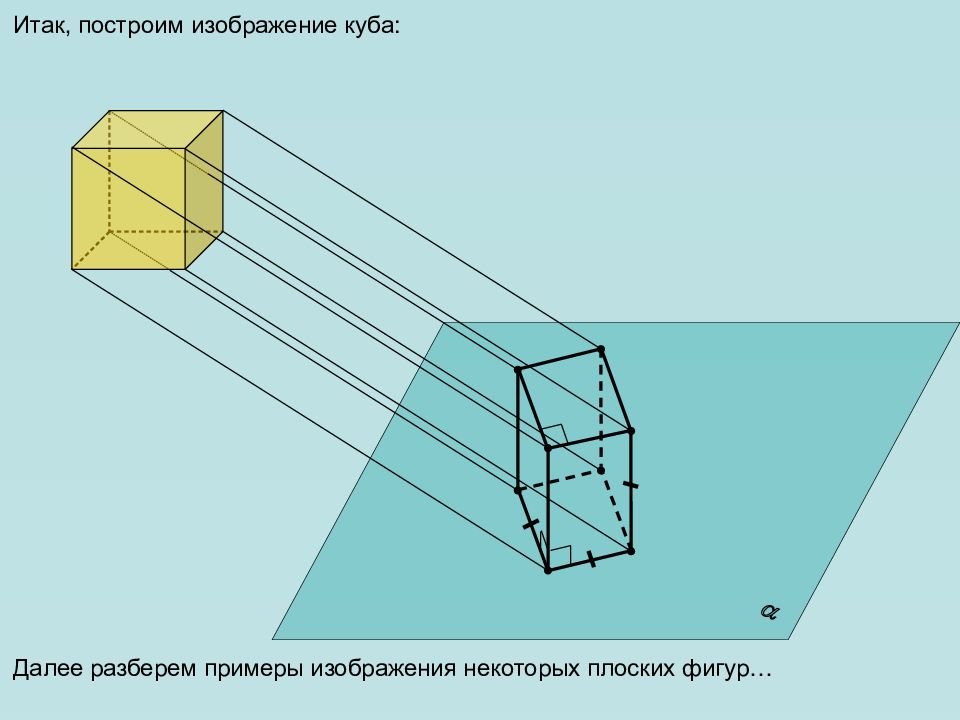
Итак, построим изображение куба: Далее разберем примеры изображения некоторых плоских фигур…
Слайд 21
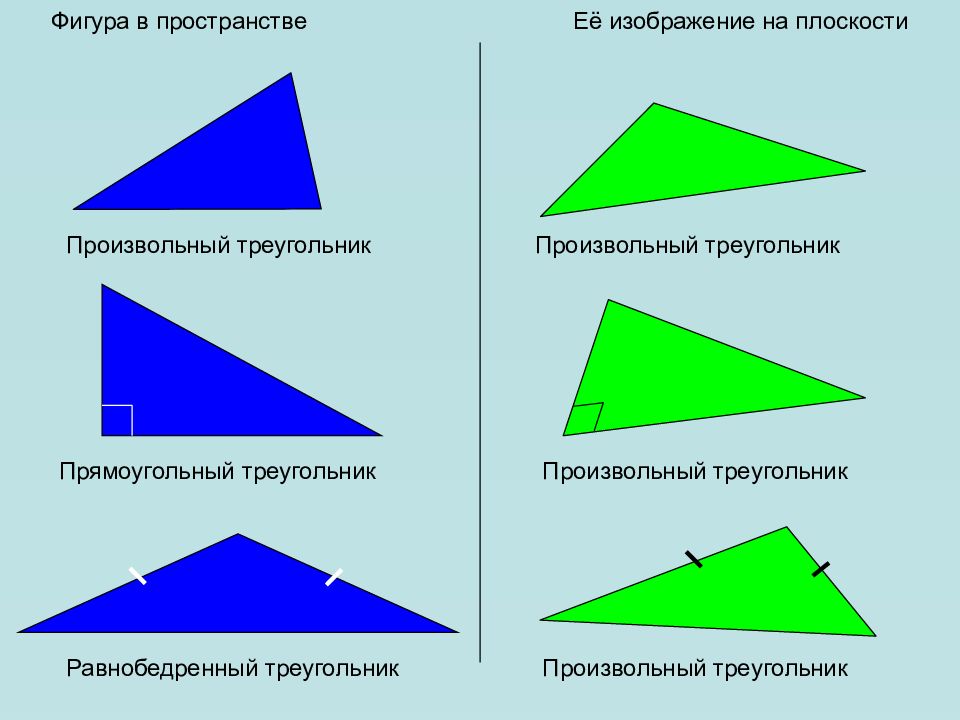
Фигура в пространстве Её изображение на плоскости Произвольный треугольник Произвольный треугольник Прямоугольный треугольник Произвольный треугольник Равнобедренный треугольник Произвольный треугольник
Слайд 22
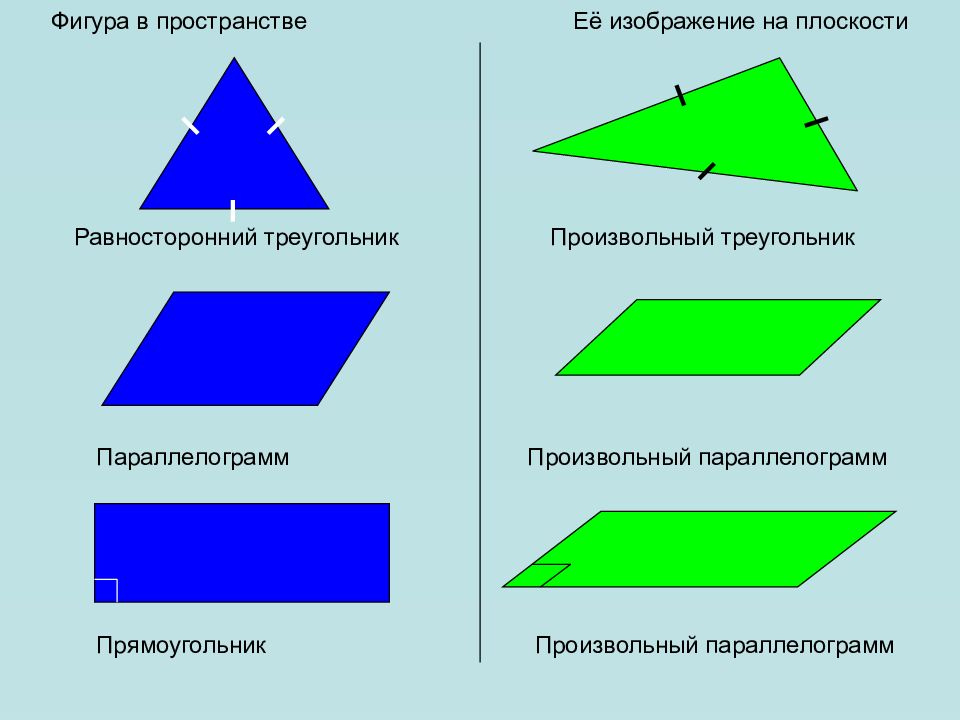
Фигура в пространстве Её изображение на плоскости Равносторонний треугольник Произвольный треугольник Параллелограмм Произвольный параллелограмм Прямоугольник Произвольный параллелограмм
Слайд 23
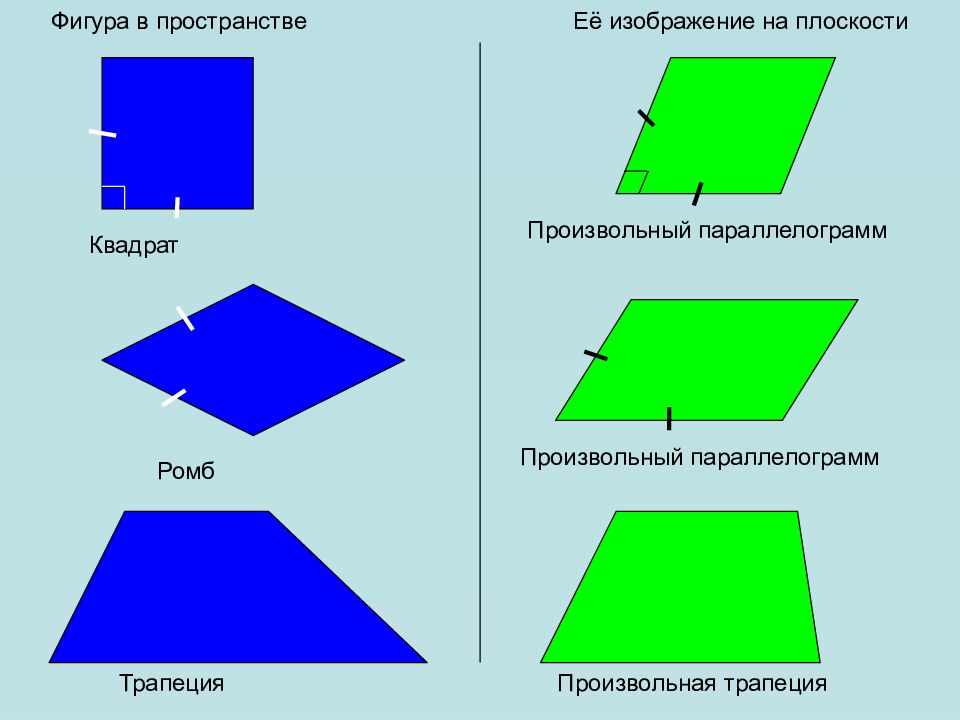
Фигура в пространстве Её изображение на плоскости Квадрат Произвольный параллелограмм Трапеция Произвольная трапеция Произвольный параллелограмм Ромб
Слайд 24
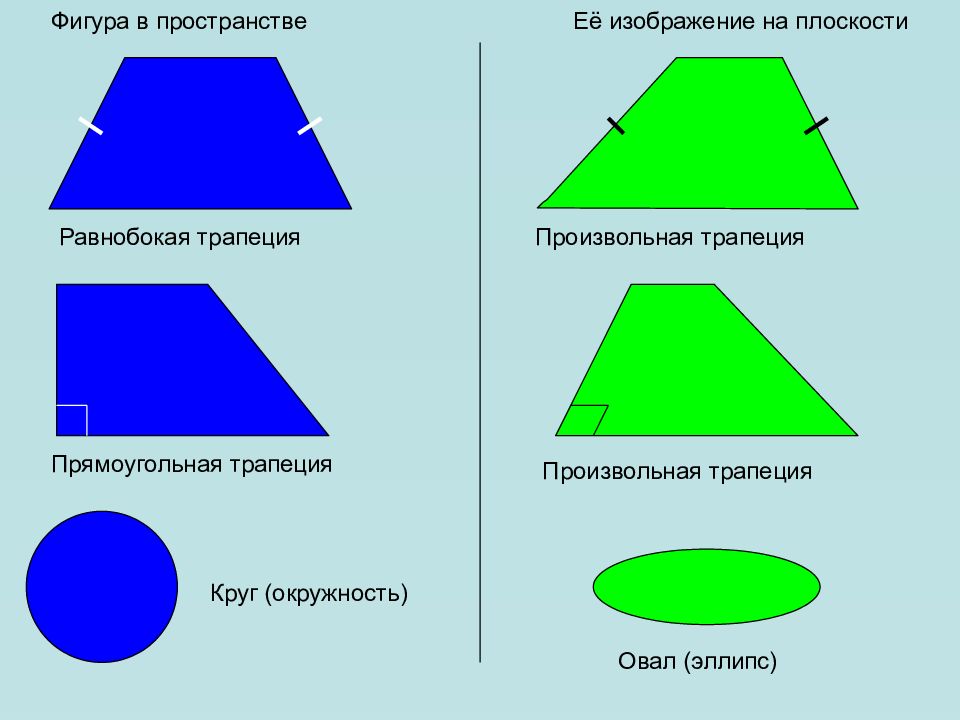
Фигура в пространстве Её изображение на плоскости Равнобокая трапеция Произвольная трапеция Прямоугольная трапеция Произвольная трапеция Круг (окружность) Овал (эллипс)
Слайд 25
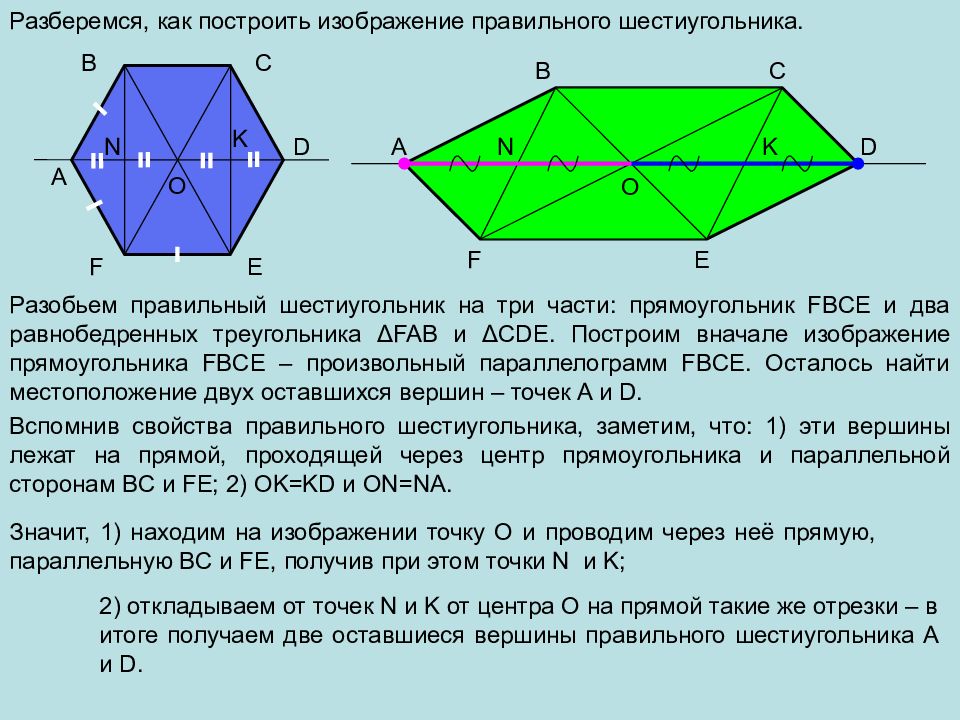
A B C D E F O Разберемся, как построить изображение правильного шестиугольника. F A B C D E Разобьем правильный шестиугольник на три части: прямоугольник FBCE и два равнобедренных треугольника Δ FAB и Δ CDE. Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE. Осталось найти местоположение двух оставшихся вершин – точек A и D. Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE ; 2) OK=KD и ON=NA. K N Значит, 1) находим на изображении точку О и проводим через неё прямую, параллельную BC и FE, получив при этом точки N и K ; O N K 2) откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D.
Слайд 26
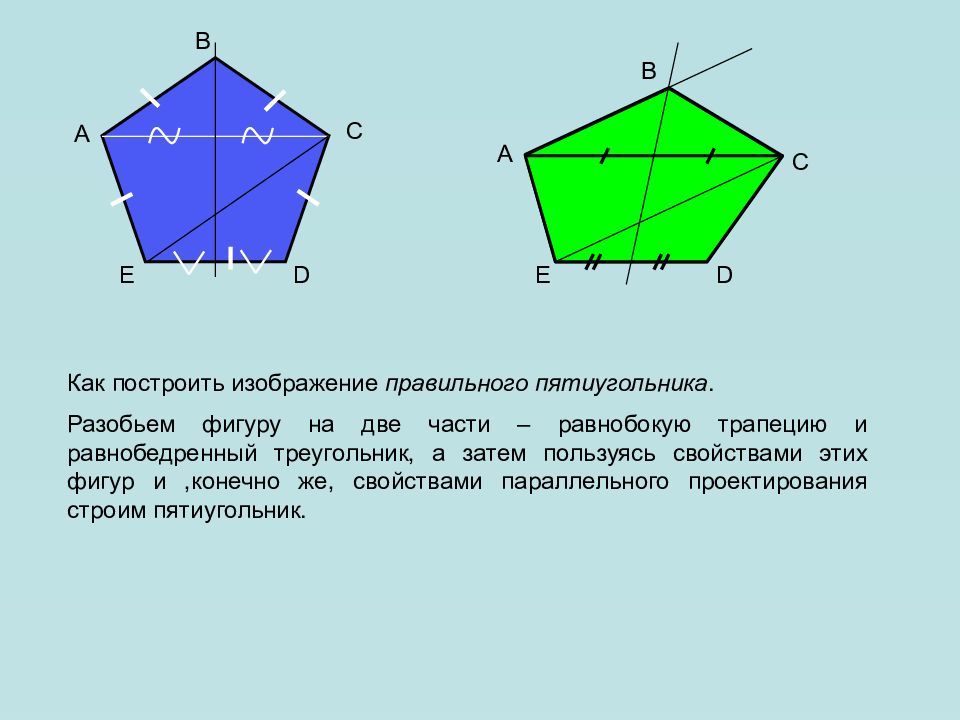
A B C D E Как построить изображение правильного пятиугольника. Разобьем фигуру на две части – равнобокую трапецию и равнобедренный треугольник, а затем пользуясь свойствами этих фигур и,конечно же, свойствами параллельного проектирования строим пятиугольник. A C D E B
Слайд 27
S AB 1 C =S ABC cos Теорема 16: Площадь ортогональной проекции треугольника равна произведению площади треугольника на косинус угла между их плоскостями. Дано: АВС АВС1 – ортогональная проекция на плоскость . Доказать:
Слайд 28
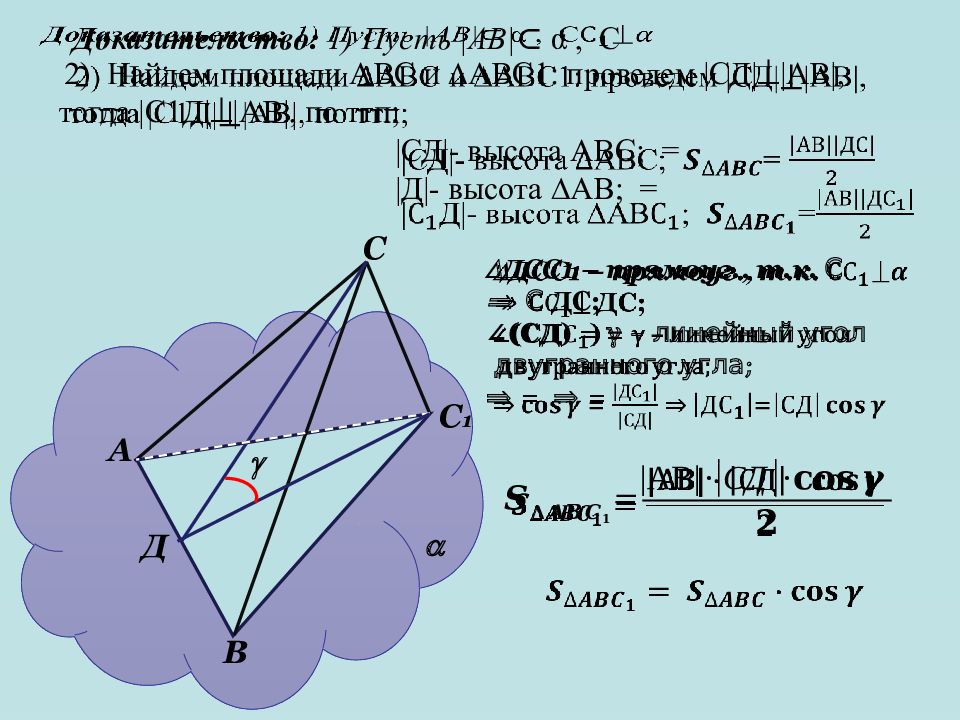
Д А С С 1 В Доказательство: 1) Пусть |АВ| ⊂ α, С 2 ) Найдем площади АВС и АВС1: проведем |СД| ⟘|АВ|, тогда |С1Д| ⟘|АВ|, по ттп ; |СД|- высота АВС; = | Д|- высота АВ ; = ДСС1 – прямоуг., т.к. С ⇒ С ДС; ∠(СД ) = γ – линейный угол двугранного угла; ⇒ = ⇒ =
Слайд 29: Теорема:
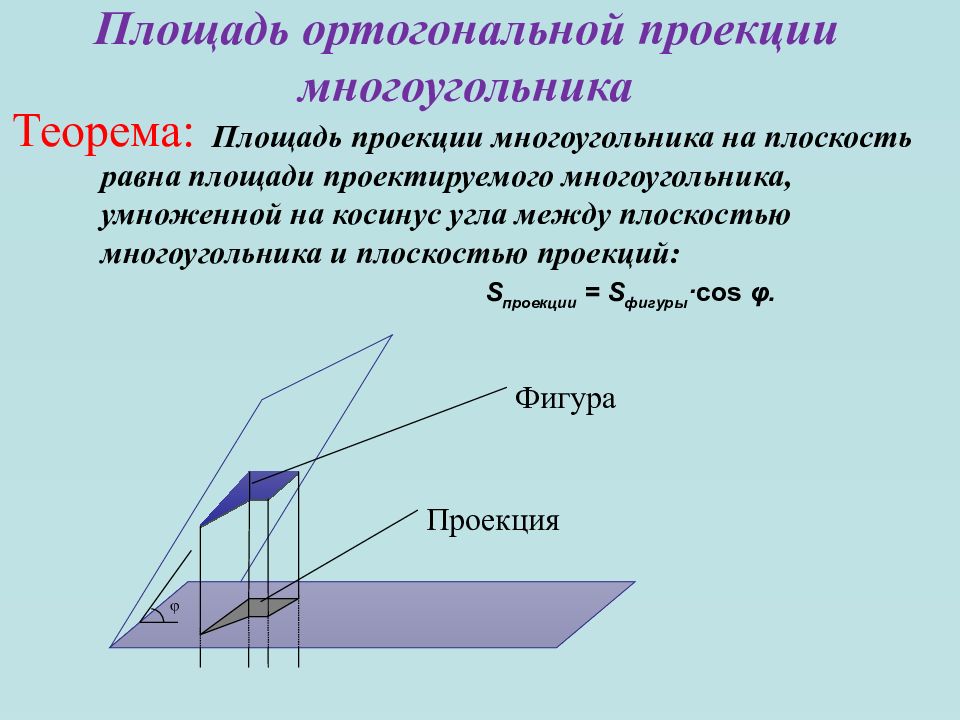
Площадь проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций: S проекции = S фигуры · cos φ. φ Фигура Проекция Площадь ортогональной проекции многоугольника
Слайд 30
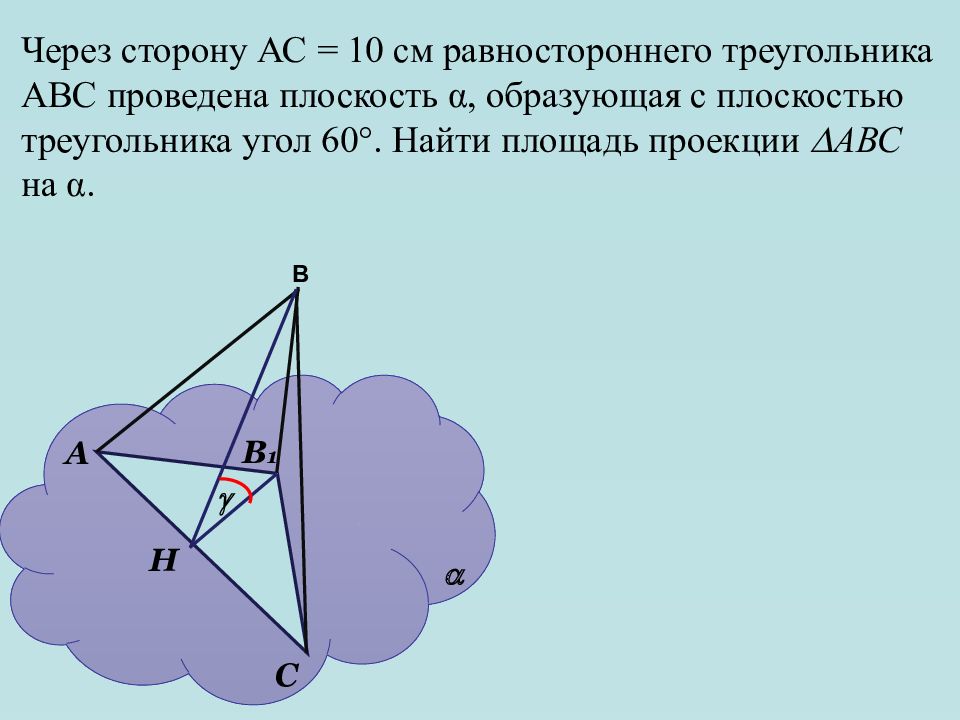
Через сторону АС = 10 см равностороннего треугольника АВС проведена плоскость α, образующая с плоскостью треугольника угол 60 °. Найти площадь проекции АВС на α. А С В 1 Н В