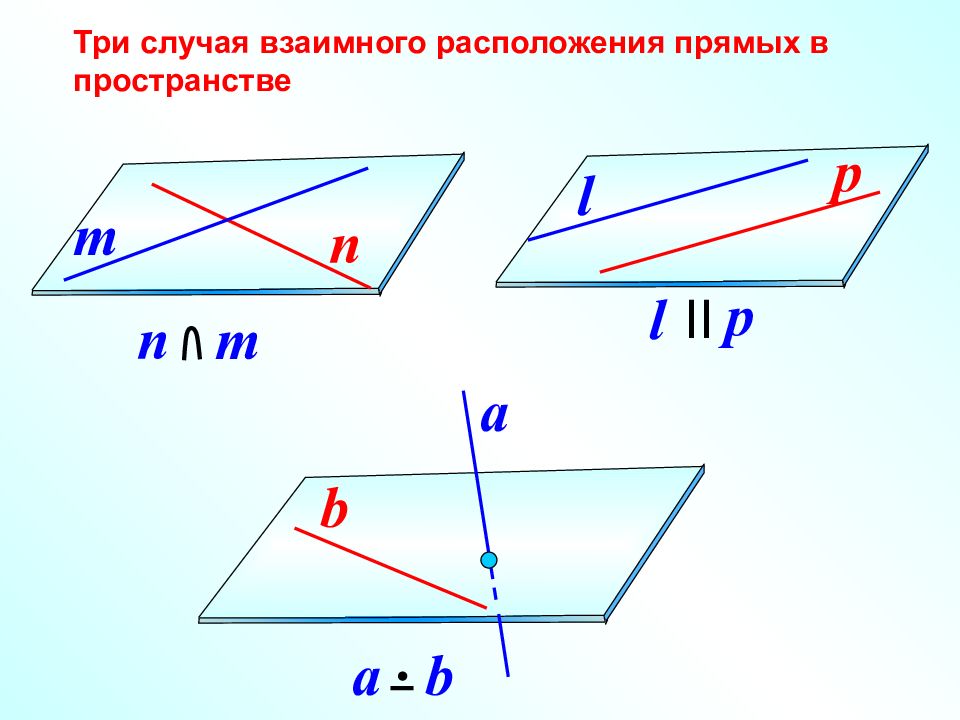
b a b Три случая взаимного расположения прямых в пространстве n m l p n m l p II a
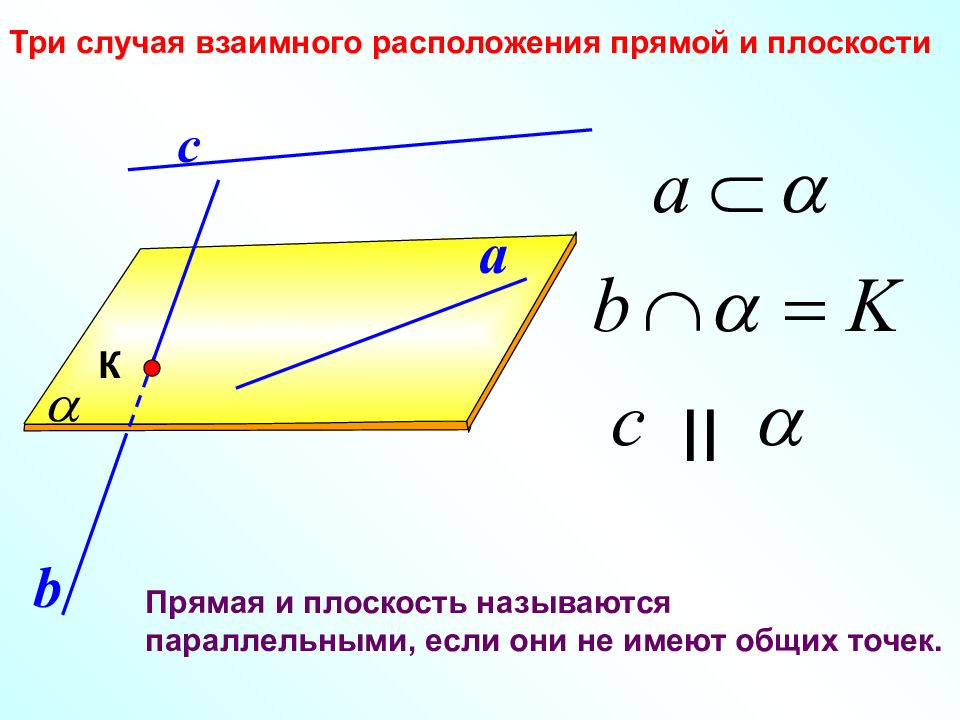
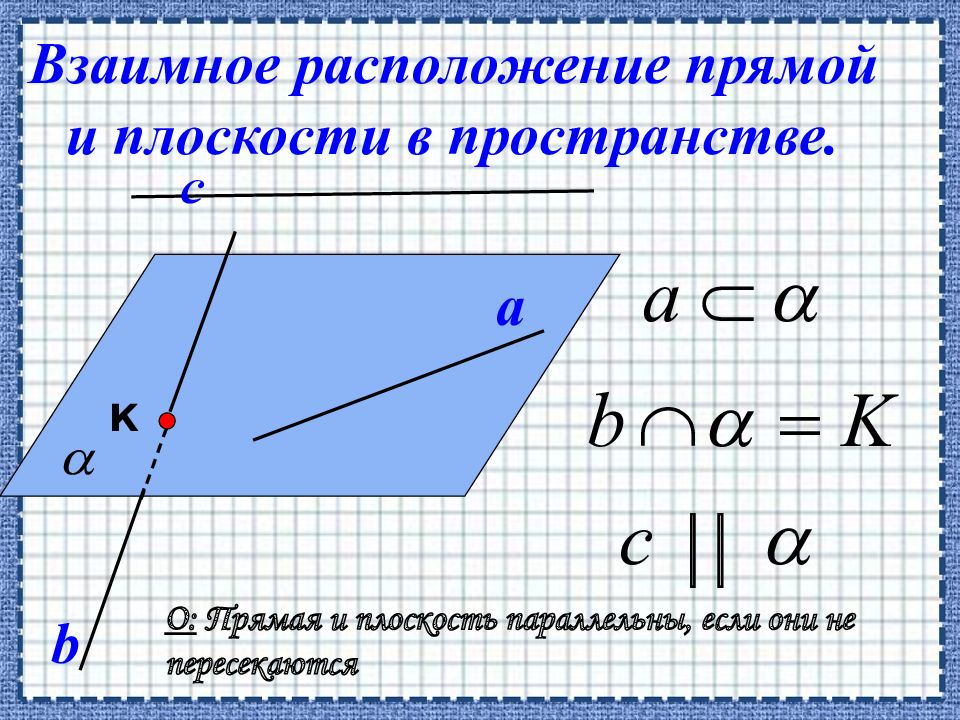
a с Три случая взаимного расположения прямой и плоскости II b К Прямая и плоскость называются параллельными, если они не имеют общих точек.
Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори, Мурманской обл. Параллельность прямой и плоскости Геометрия 10
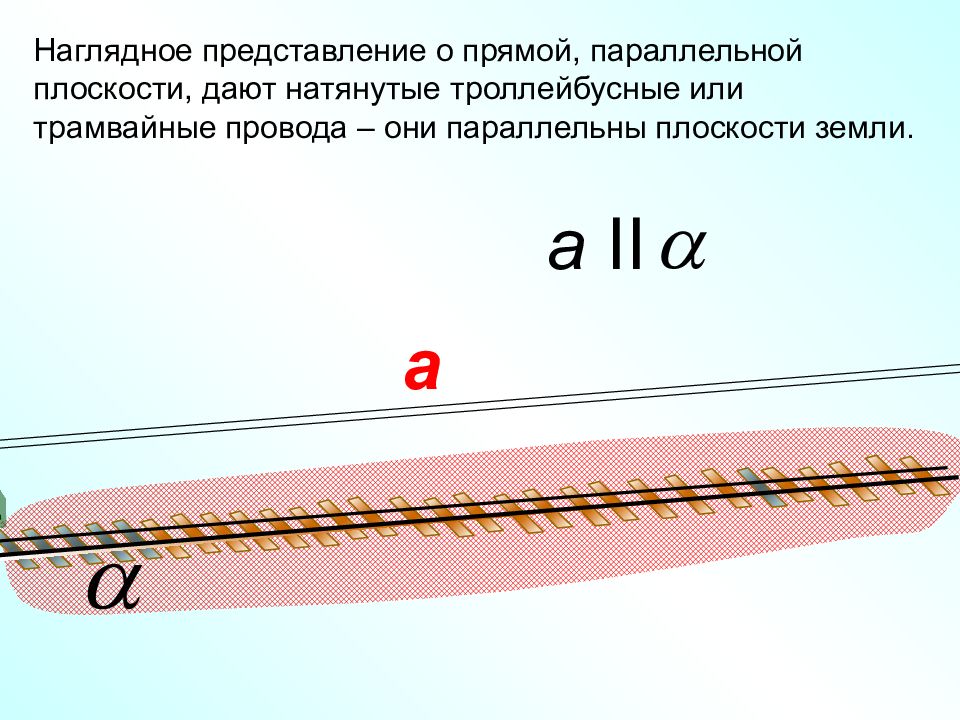
а a II Наглядное представление о прямой, параллельной плоскости, дают натянутые троллейбусные или трамвайные провода – они параллельны плоскости земли.
а
а b
А В С D D 1 С 1 В 1 А 1 Назовите прямые, параллельные данной плоскости
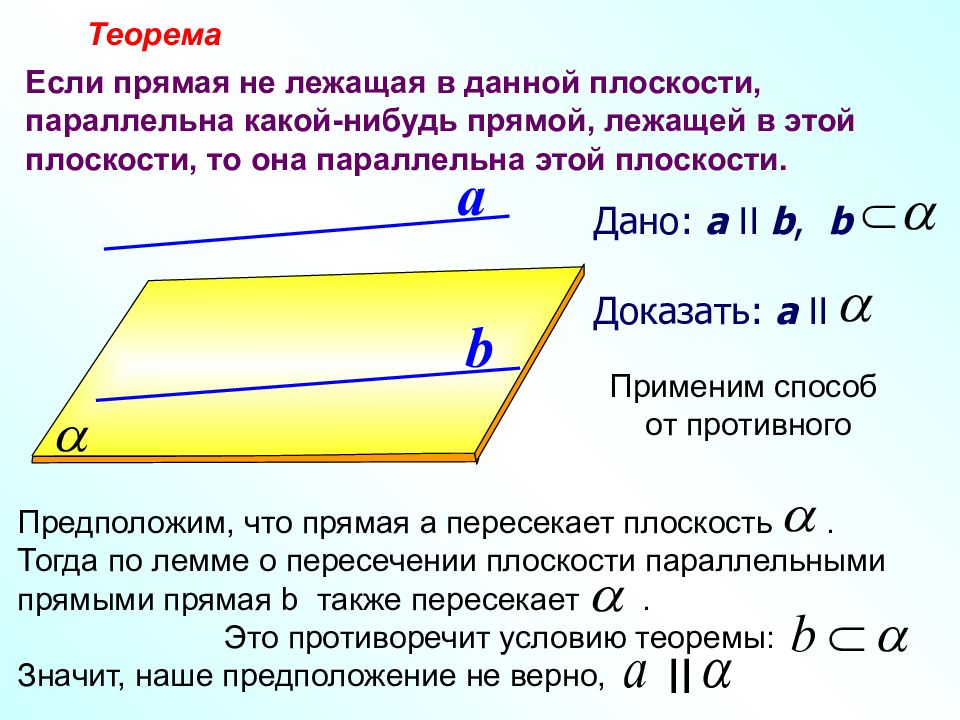
Дано: a II b, b Доказать: a II a b Теорема Если прямая не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна этой плоскости. Применим способ от противного Предположим, что прямая а пересекает плоскость. Тогда по лемме о пересечении плоскости параллельными прямыми прямая b также пересекает. Это противоречит условию теоремы: Значит, наше предположение не верно, II
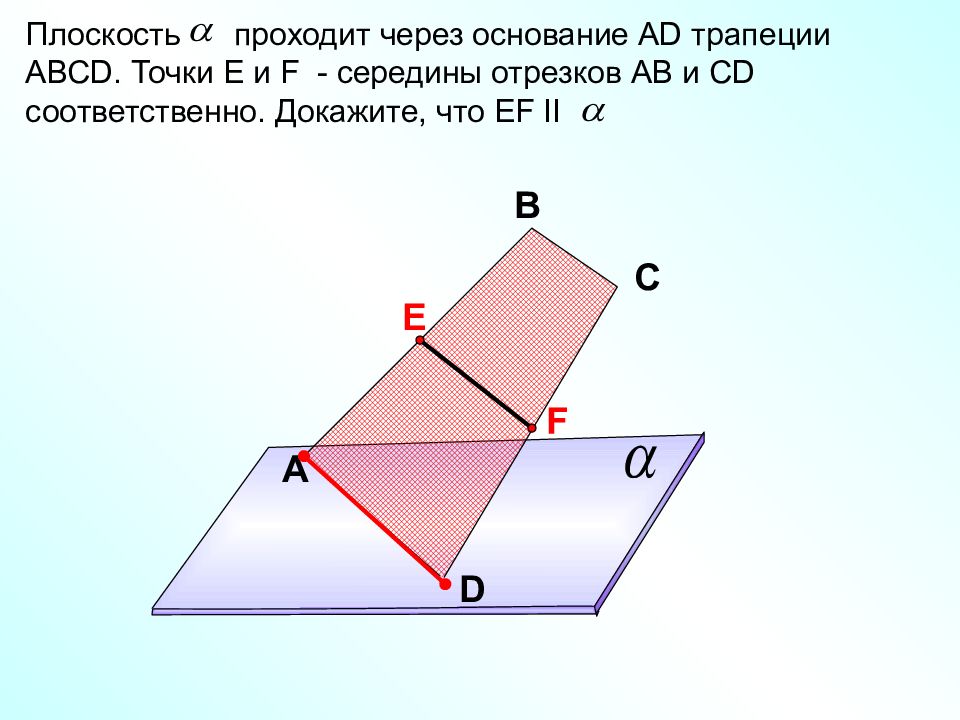
A В С D Плоскость проходит через основание А D трапеции АВС D. Точки Е и F - середины отрезков АВ и С D соответственно. Докажите, что EF II Е F
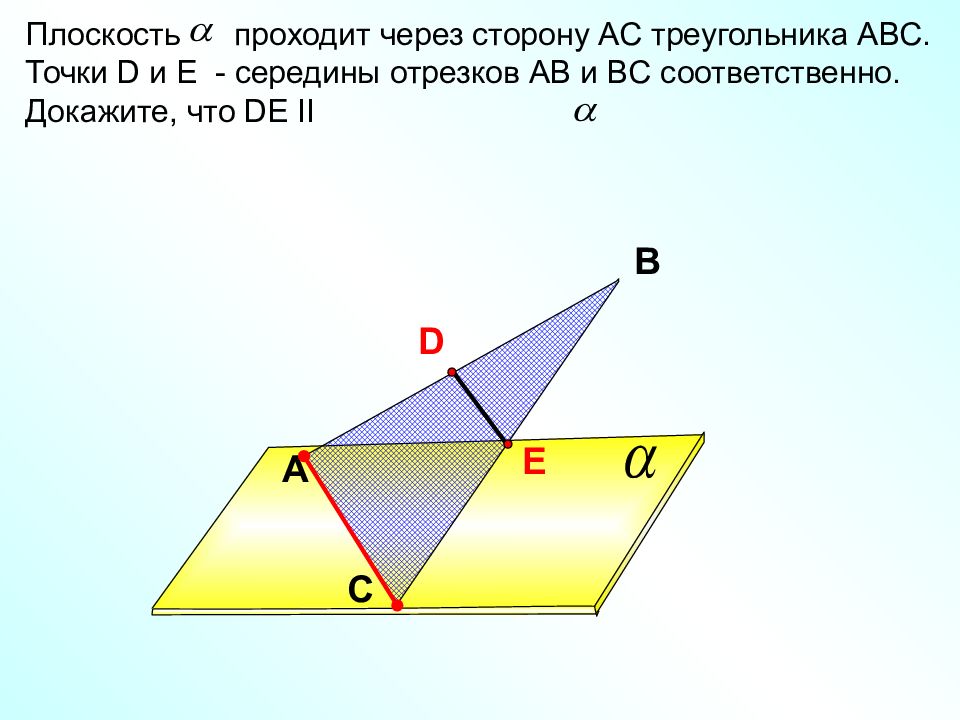
A В С Плоскость проходит через сторону АС треугольника АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE II D E
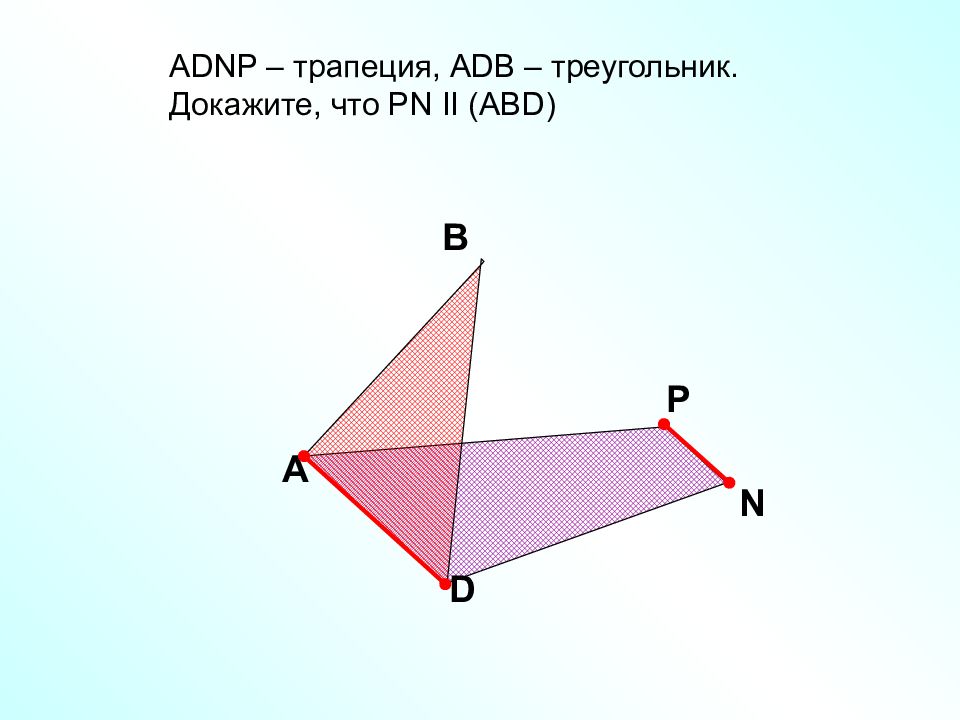
A В D А DNP – трапеция, А DB – треугольник. Докажите, что Р N II (ABD) Р N
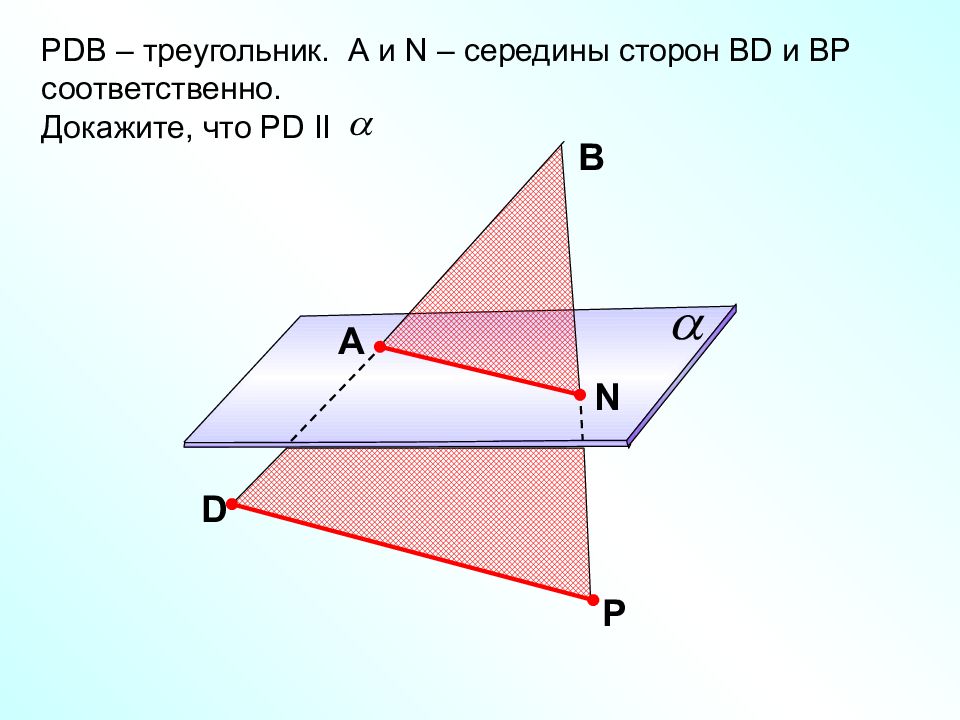
Р DB – треугольник. А и N – середины сторон В D и ВР соответственно. Докажите, что Р D II D Р В A N
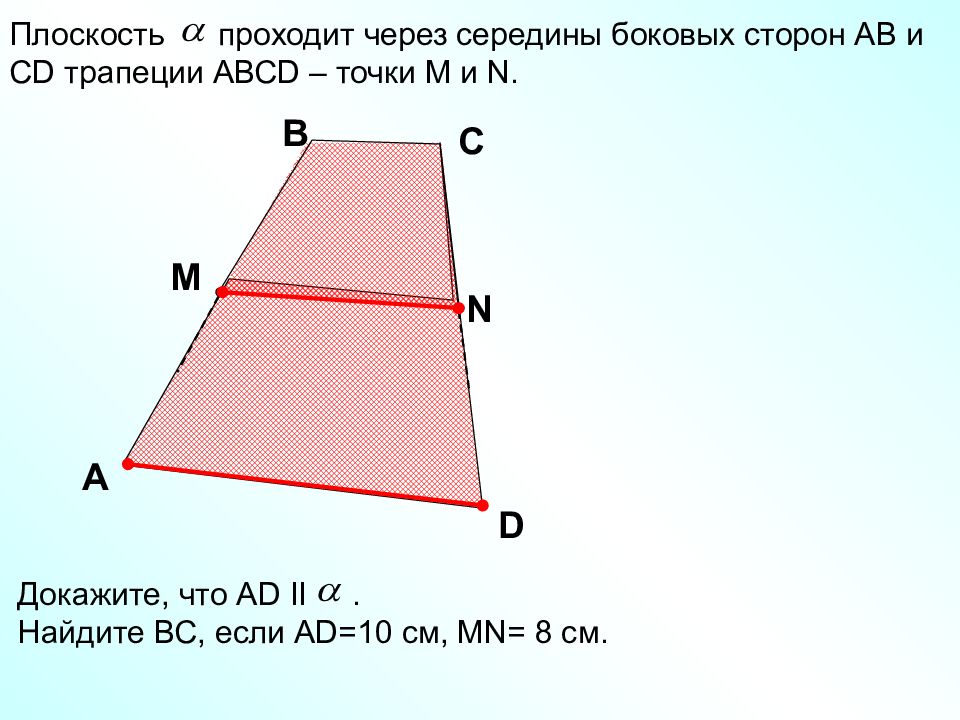
Плоскость проходит через середины боковых сторон АВ и С D трапеции АВС D – точки М и N. A D С M N Докажите, что А D II. Найдите ВС, если А D= 10 см, MN= 8 см. B
Домашняя работа:
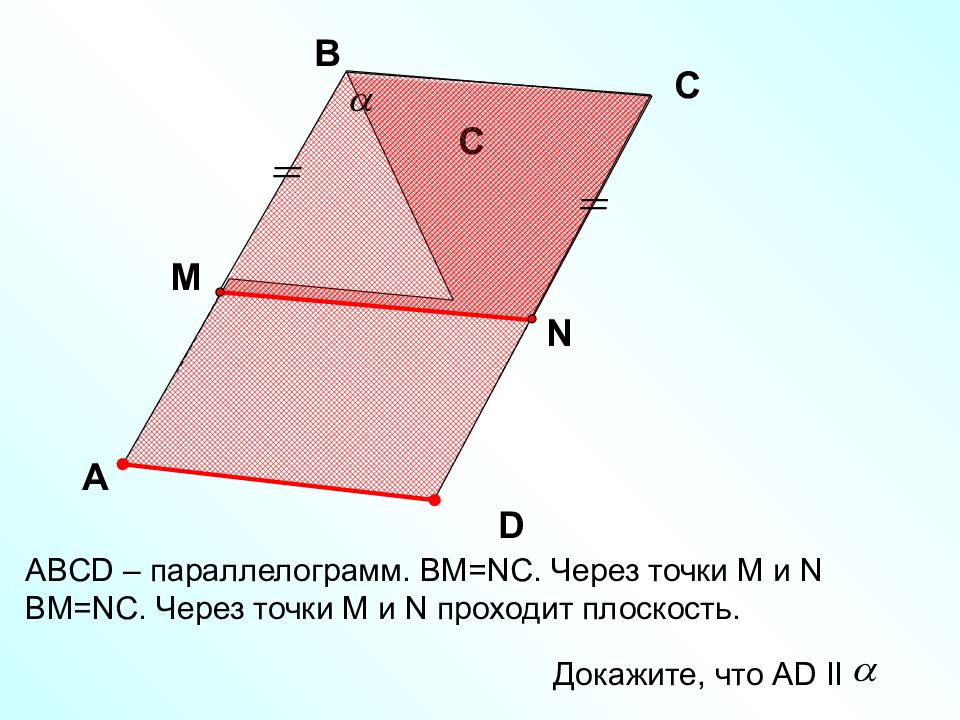
ABCD – параллелограмм. ВМ= NC. Через точки М и N ВМ= NC. Через точки М и N проходит плоскость. A D С C Докажите, что А D II B M N
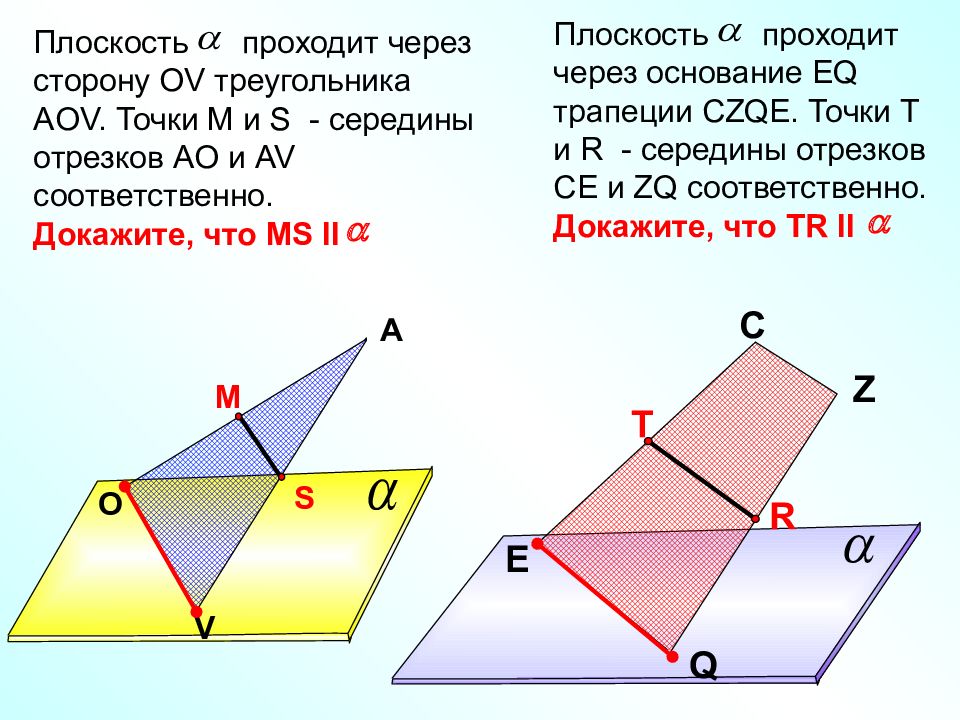
O A V M S Плоскость проходит через сторону OV треугольника А OV. Точки M и S - середины отрезков А O и AV соответственно. Докажите, что MS II a E C Z Q T R Плоскость проходит через основание EQ трапеции CZQE. Точки T и R - середины отрезков CE и ZQ соответственно. Докажите, что TR II a
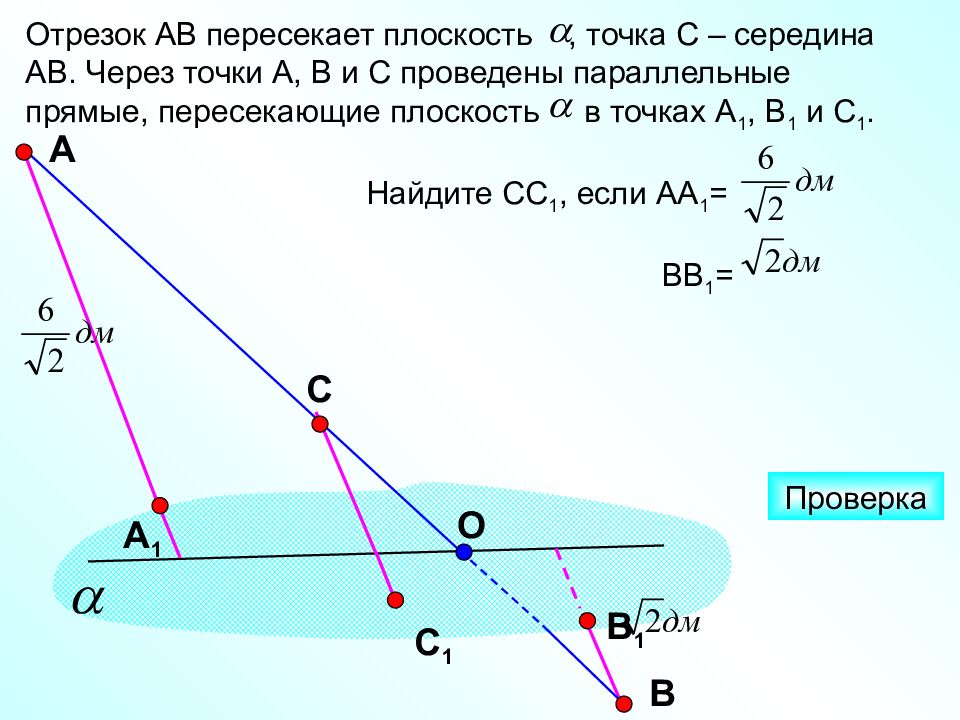
Отрезок АВ пересекает плоскость, точка С – середина АВ. Через точки А, В и С проведены параллельные прямые, пересекающие плоскость в точках А 1, В 1 и С 1. Найдите СС 1, если АА 1 = ВВ 1 = А С Проверка А 1 С 1 В 1 В О
