Первый слайд презентации
Тема «Решение систем линейных уравнений методом Крамера»
Слайд 2: 1. Область применения метода Крамера
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения. Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение. 1. Область применения метода Крамера
Слайд 3
Рассмотрим систему двух уравнений с двумя неизвестными x и y : Числа Такую запись системы, в которой свободные члены находятся в правых частях, будем называть стандартной. Определение: Решением системы двух уравнений с двумя неизвестными называется всякая пара чисел (x,y), обращающая эту систему в тождество. Если существует только одна такая пара, то решение называется единственным. Например, называются коэффициентами системы ; - свободными членами. В записи коэффициентов индекс называется номером строки (уравнения), а индекс называется номером столбца (неизвестного). (1)
Слайд 4
Введем в рассмотрение следующие три определителя для системы (1): Определитель, составленный из коэффициентов системы, называется определителем системы. Определители,,полученные из определителя системы заменой соответствующего столбца столбцом свободных членов, называются вспомогательными. 2. Теорема Крамера
Слайд 5
Теорема (правило Крамера ). Есл и 0, то система имеет единственное решение, которое находится по формулам Данные формулы называются формулами Крамера. Пример 1. Решить по правилу Крамера систему уравнений Решение. Вычислим определитель системы
Слайд 6
Так как определитель системы отличен от нуля, то, согласно правилу Крамера, решение системы существует, единственно и находится по формулам Крамера. Вычислим определители : По формулам Крамера находим неизвестные и
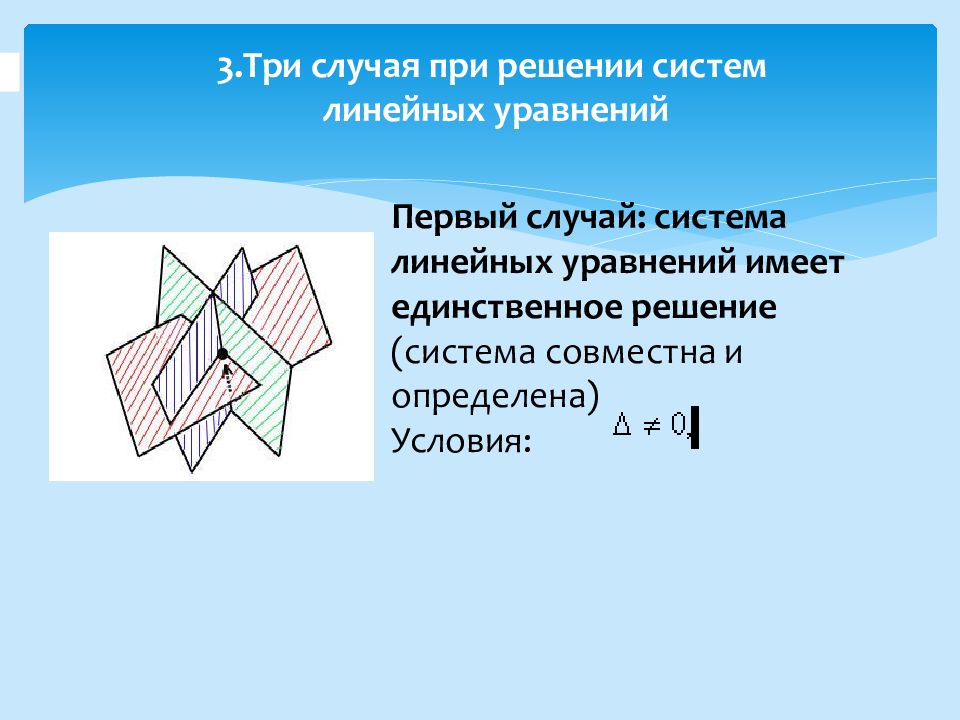
Первый случай: система линейных уравнений имеет единственное решение (система совместна и определена) Условия:
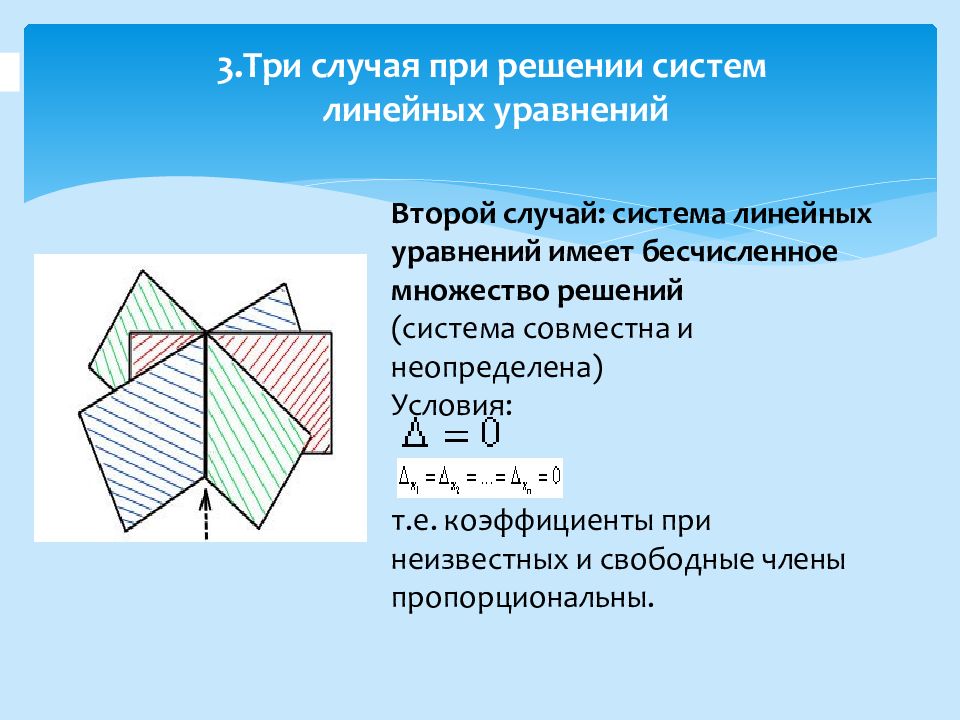
Второй случай: система линейных уравнений имеет бесчисленное множество решений (система совместна и неопределена) Условия: т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
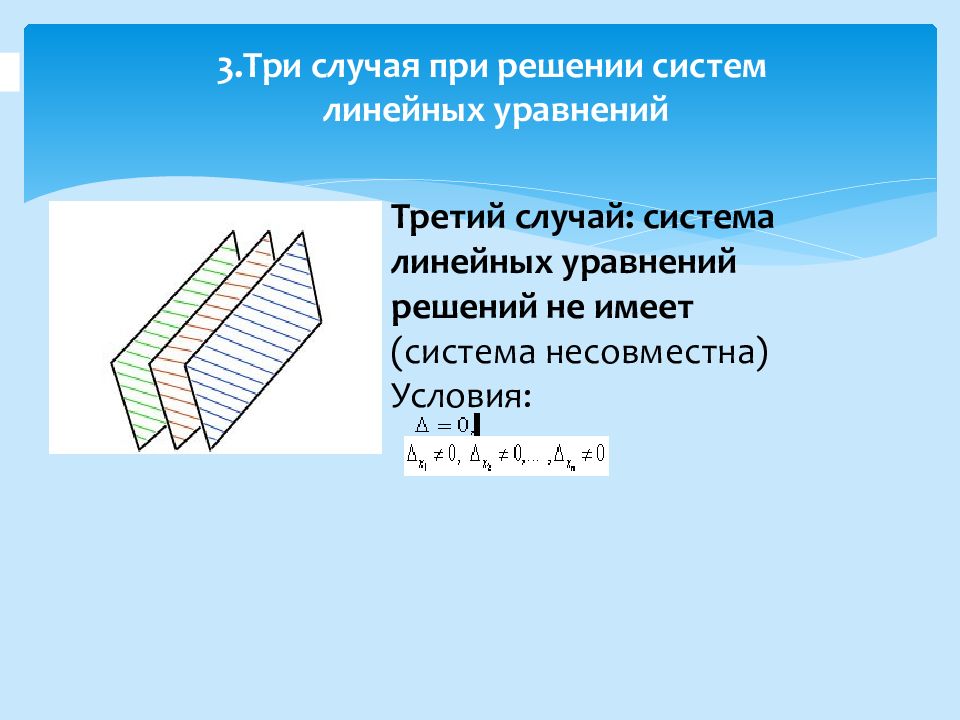
Третий случай: система линейных уравнений решений не имеет (система несовместна) Условия:
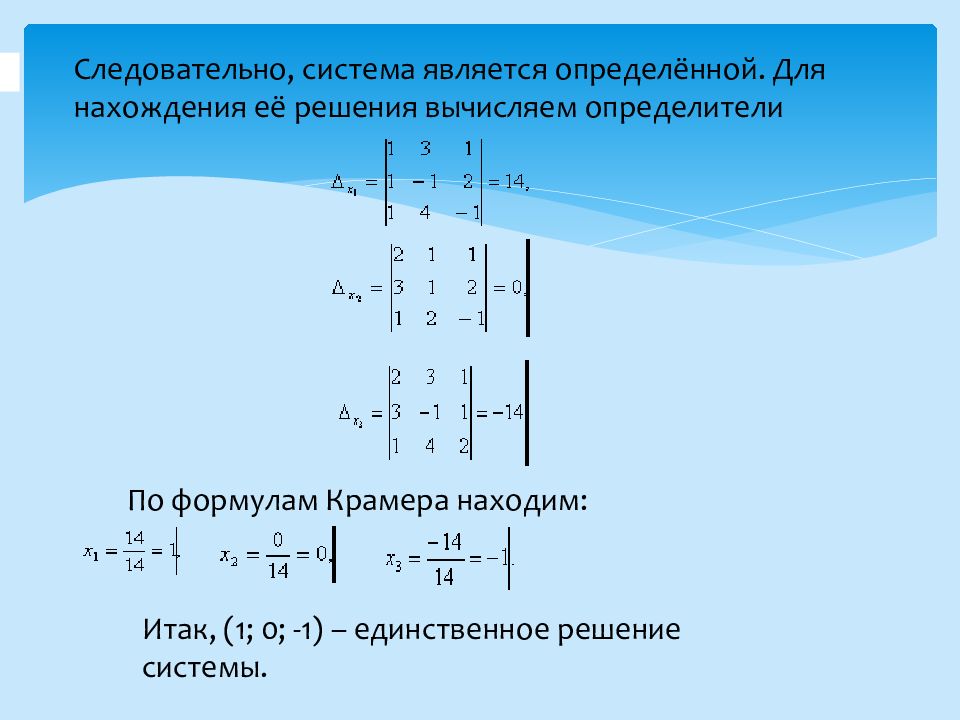
Слайд 10: 4. Примеры решения систем
Пример. Решить систему линейных уравнений методом Крамера: Решение. Находим определитель системы: