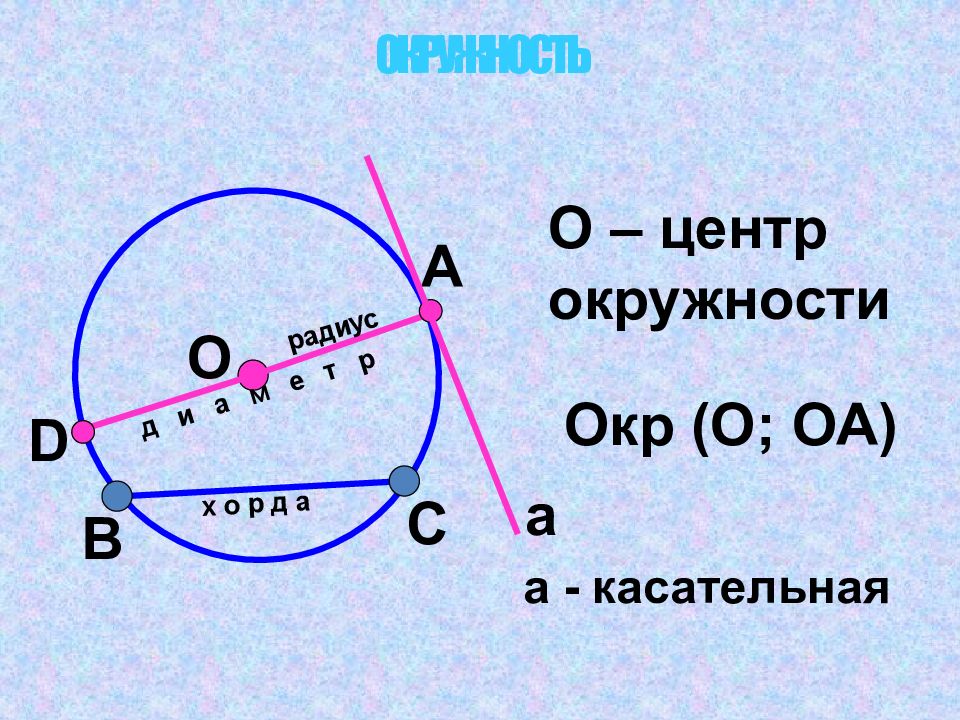
Слайд 3
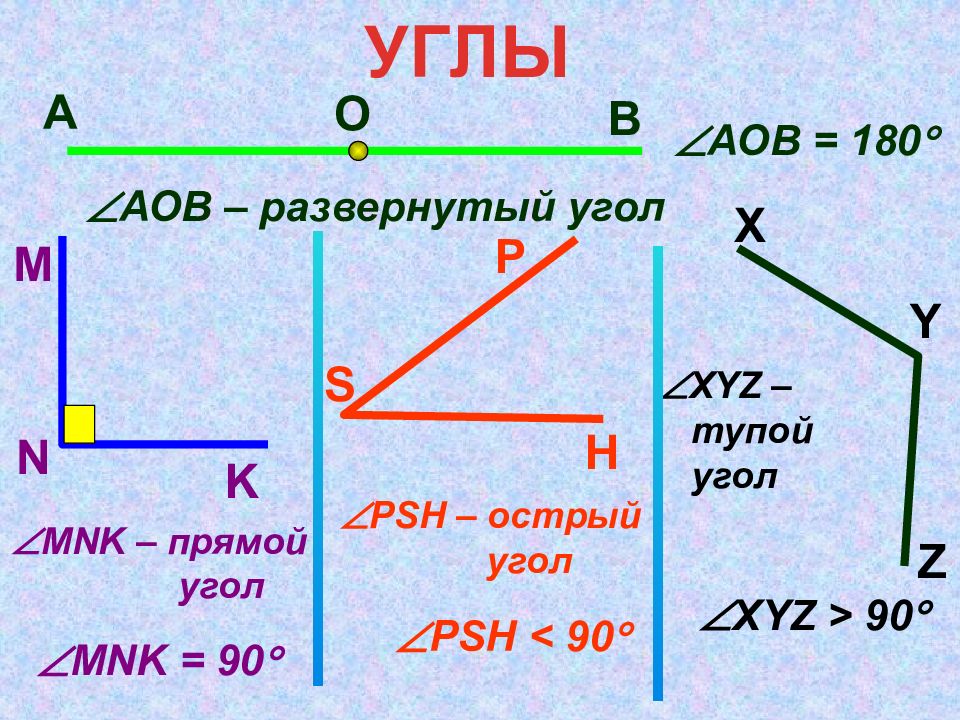
А О В АОВ – развернутый угол M N K MNK – прямой угол АОВ = 180 MNK = 9 0 P S H PSH – острый угол PSH < 9 0 X Y Z XYZ – тупой угол XYZ > 9 0 УГЛЫ
Слайд 4
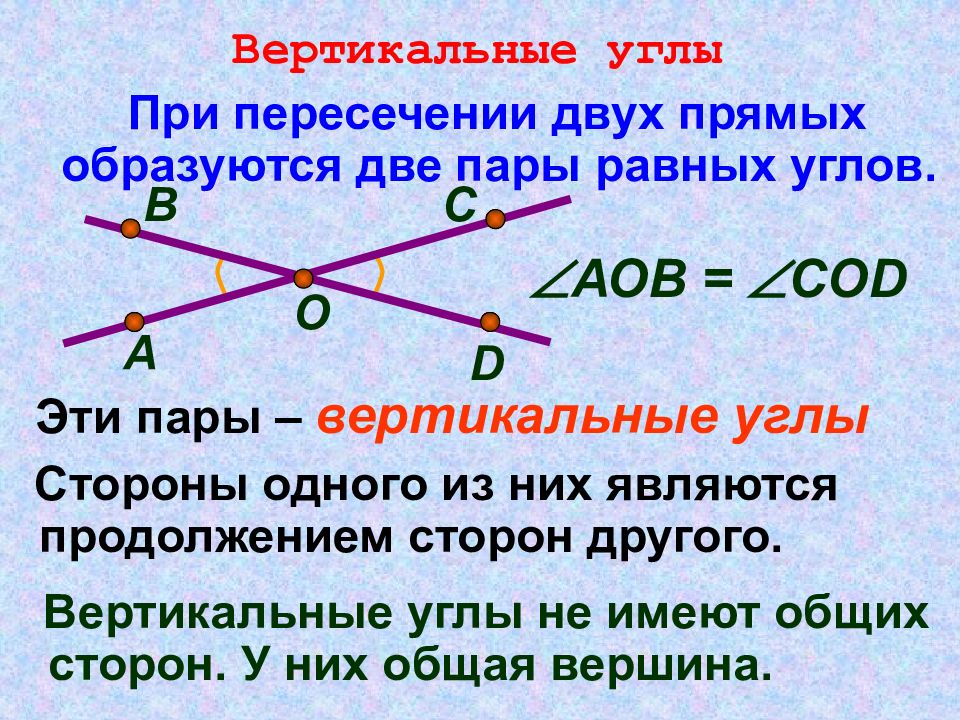
Вертикальные углы При пересечении двух прямых образуются две пары равных углов. О А С D В АО B = COD Эти пары – вертикальные углы Стороны одного из них являются продолжением сторон другого. Вертикальные углы не имеют общих сторон. У них общая вершина.
Слайд 5
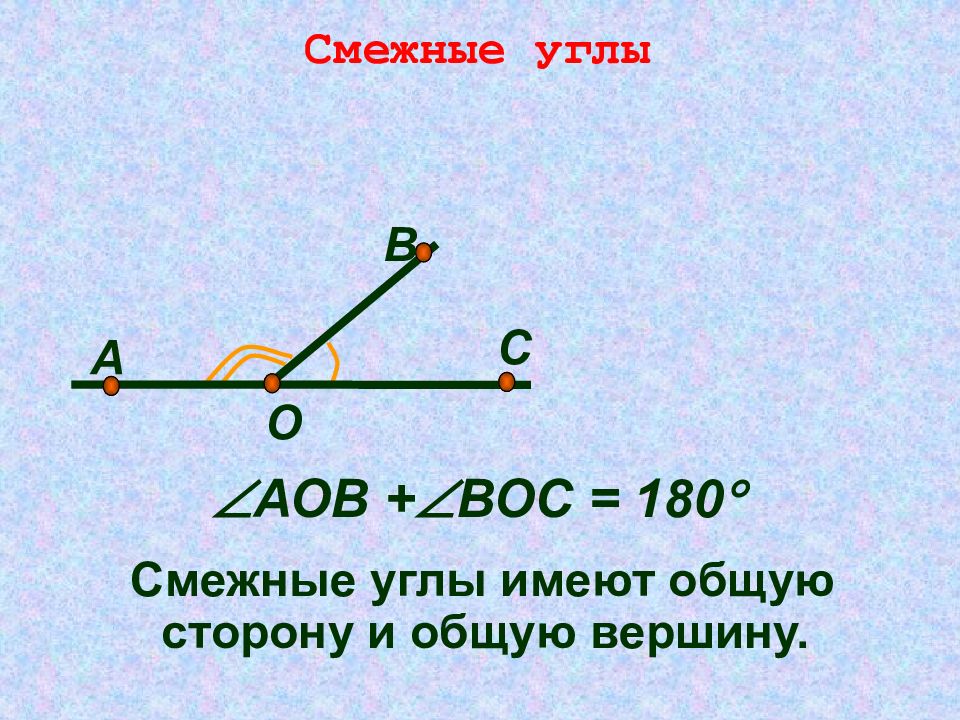
Смежные углы О А В С АО B + ВОС = 180 Смежные углы имеют общую сторону и общую вершину.
Слайд 6
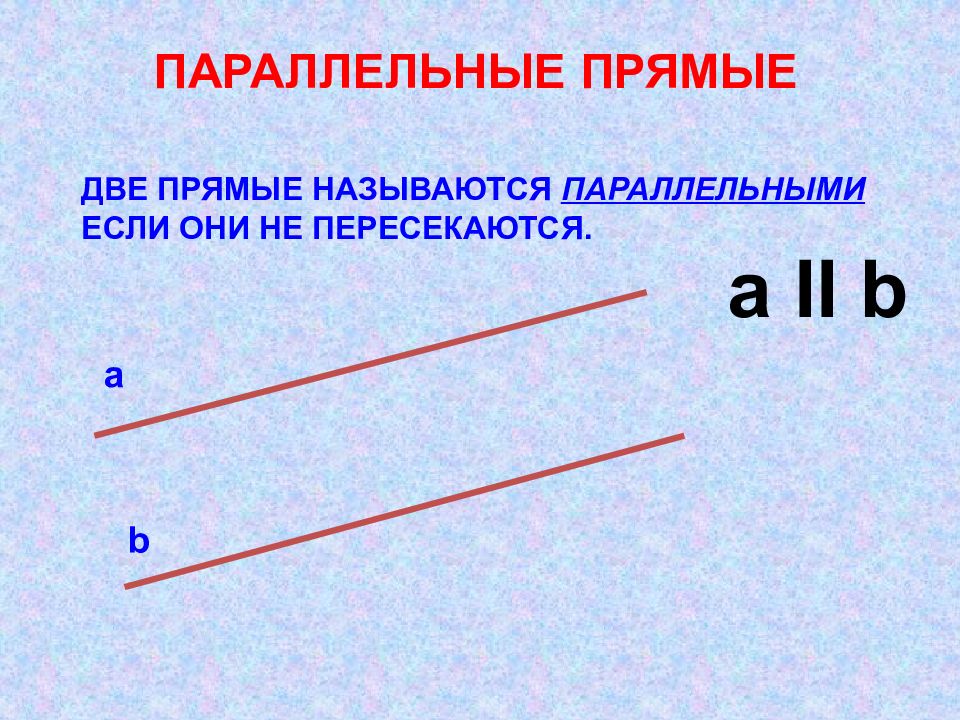
ДВЕ ПРЯМЫЕ НАЗЫВАЮТСЯ ПАРАЛЛЕЛЬНЫМИ ЕСЛИ ОНИ НЕ ПЕРЕСЕКАЮТСЯ. а b а II b ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Слайд 7
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ Две прямые называются перпендикулярными, если они пересекаются под прямым углом. а в а | в
Слайд 8
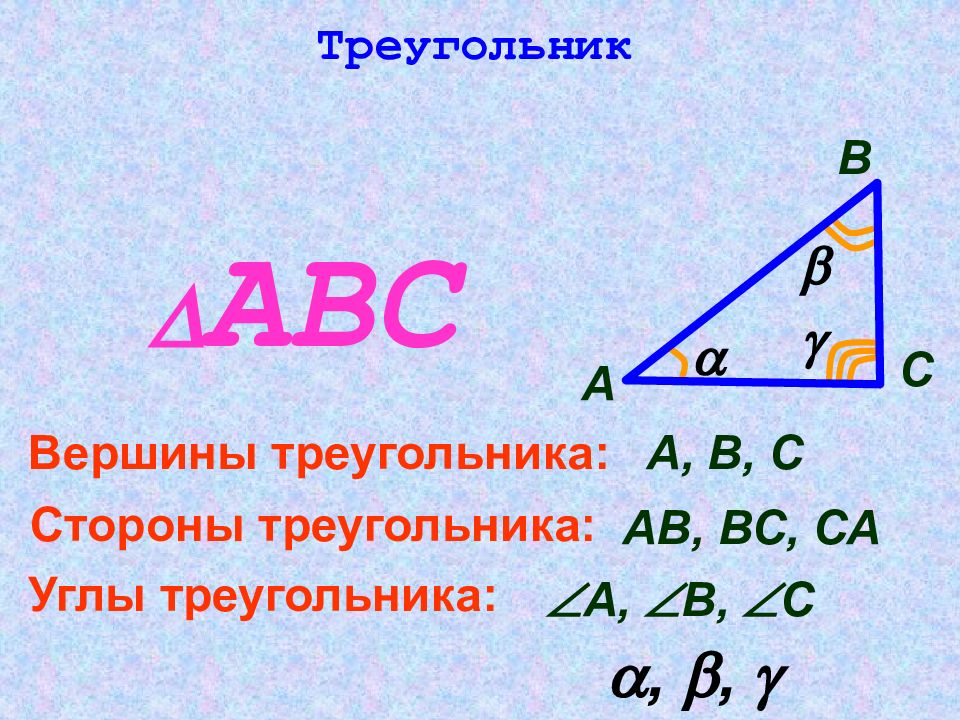
Треугольник А В С А, В, С Вершины треугольника: АВ, ВС, СА Стороны треугольника: А, В, С Углы треугольника: , , АВС
Слайд 9
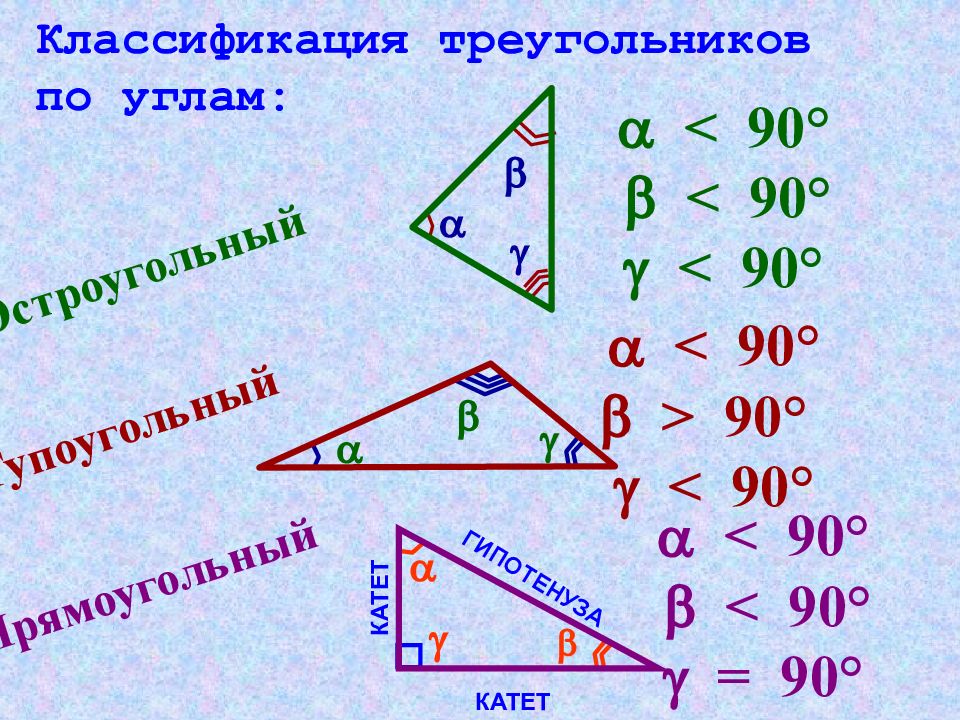
Остроугольный < 90 ° < 90° < 90° Тупоугольный < 90 ° > 90° < 90° Прямоугольный < 90 ° < 90° = 90° Классификация треугольников по углам: ГИПОТЕНУЗА КАТЕТ КАТЕТ
Слайд 10
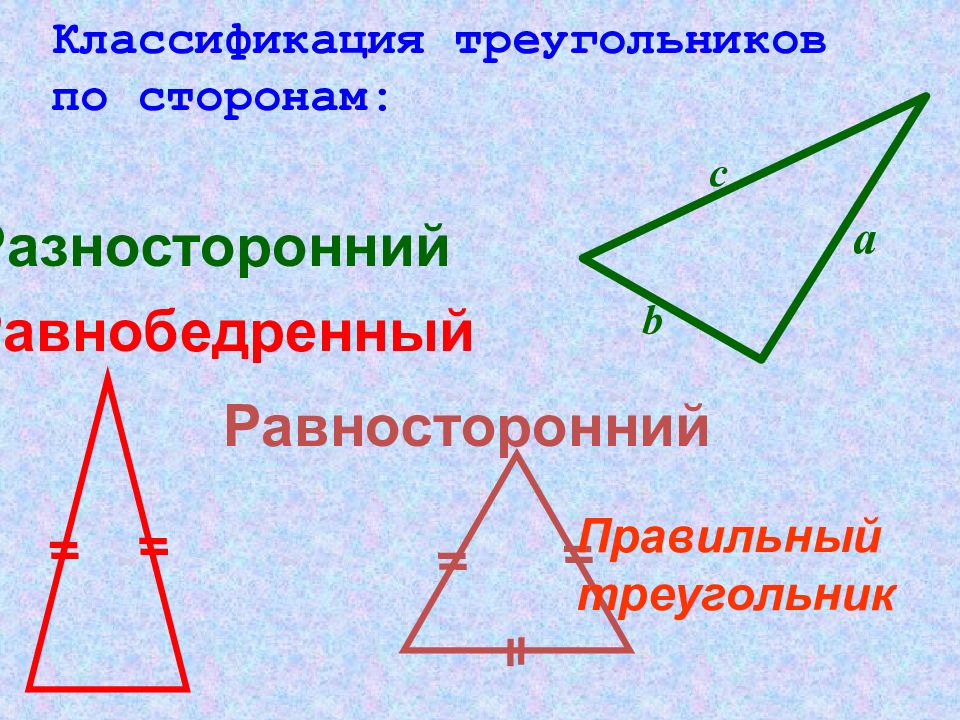
Разносторонний Равнобедренный Равносторонний а b c Классификация треугольников по сторонам: Правильный треугольник
Слайд 11
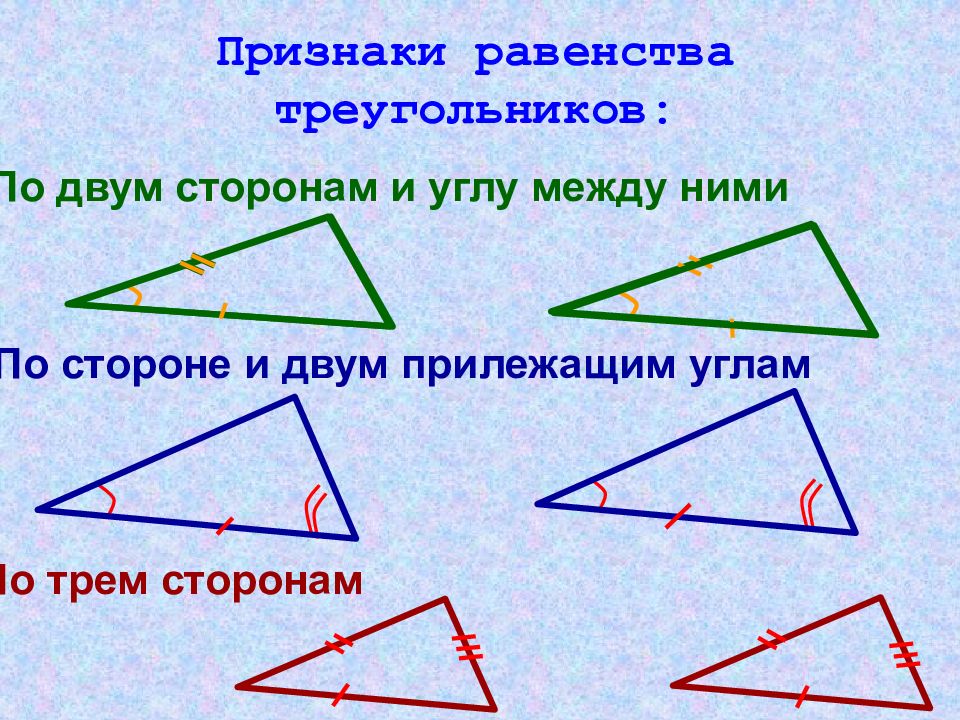
По двум сторонам и углу между ними По стороне и двум прилежащим углам По трем сторонам Признаки равенства треугольников:
Слайд 12
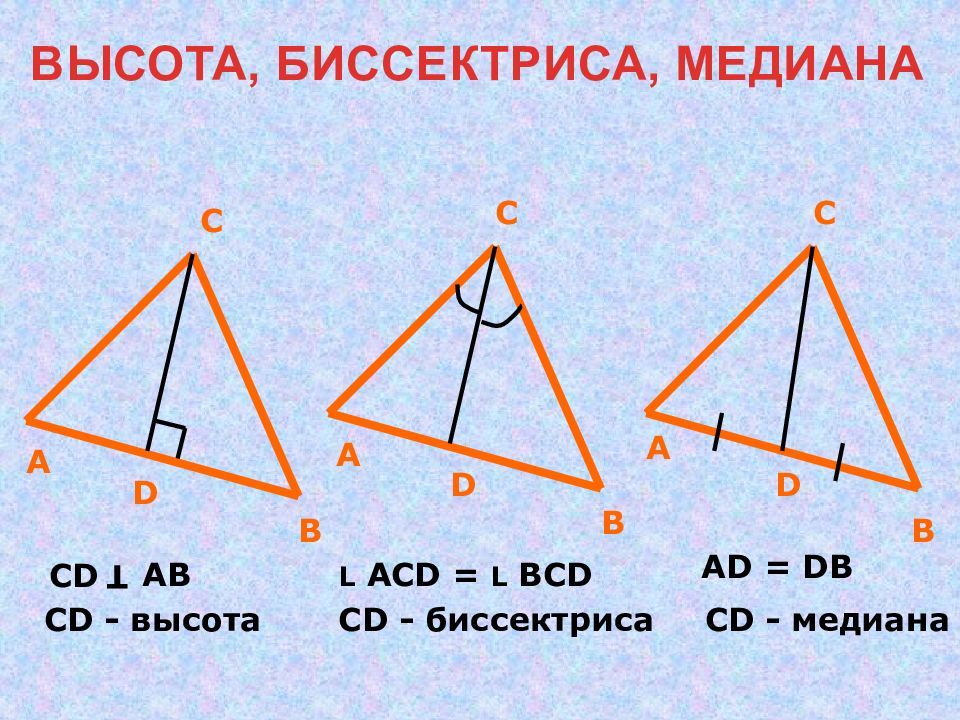
А В С А В С А В С D CD Т АВ С D - высота D L АС D = L ВС D CD - биссектриса D AD = D В С D - медиана ВЫСОТА, БИССЕКТРИСА, МЕДИАНА
Слайд 13
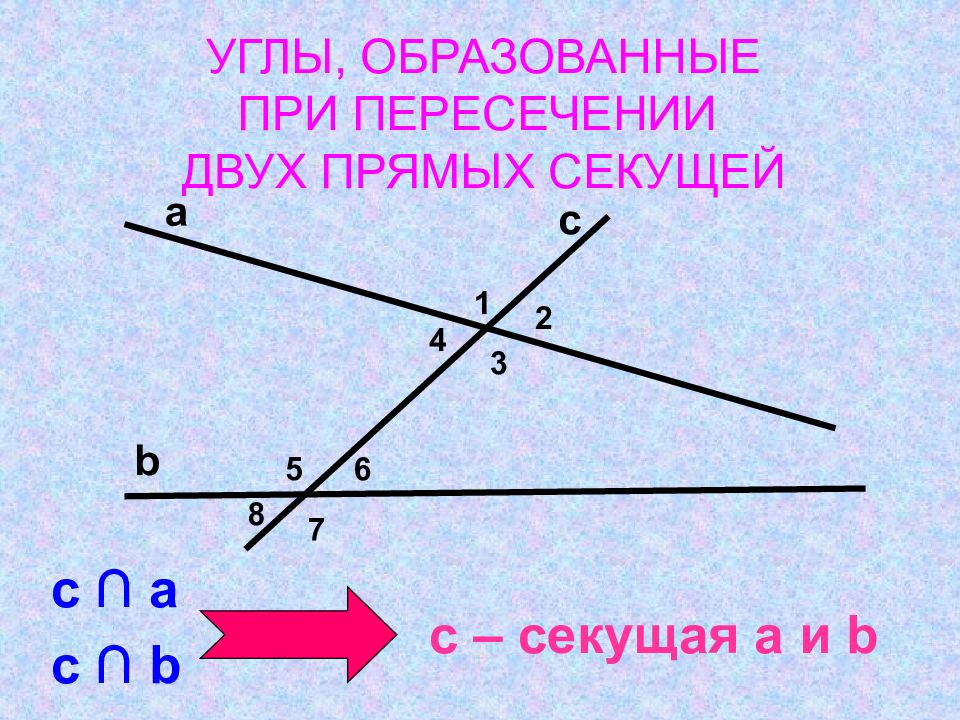
а b с с ∩ а с ∩ b с – секущая а и b 1 2 3 4 5 6 7 8 УГЛЫ, ОБРАЗОВАННЫЕ ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ
Слайд 14
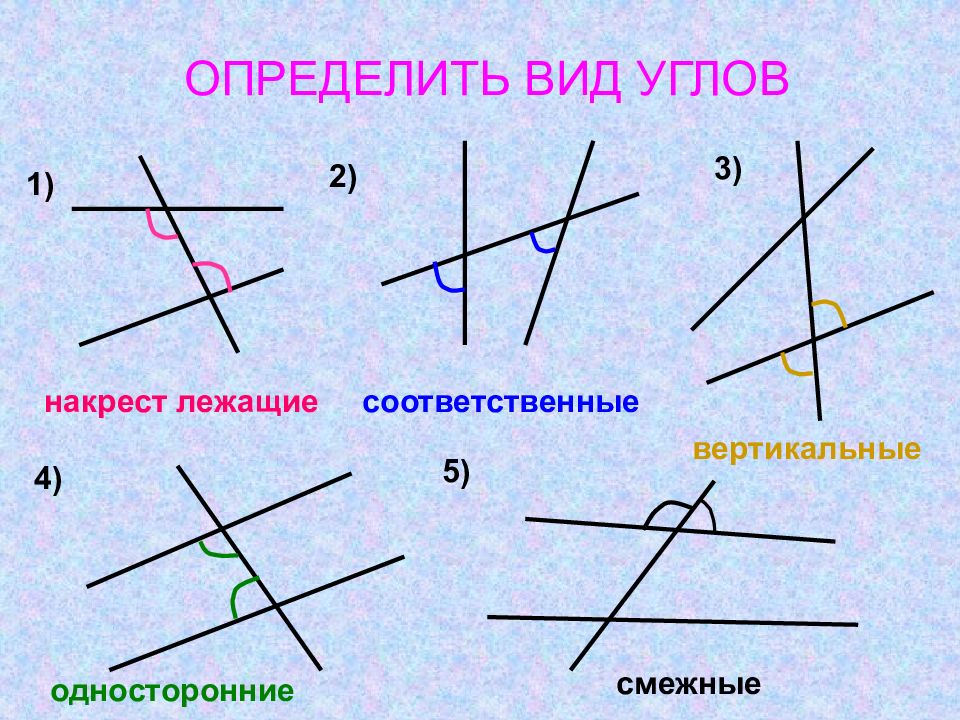
1) 2) 3) 4) накрест лежащие соответственные вертикальные односторонние 5) смежные ОПРЕДЕЛИТЬ ВИД УГЛОВ