Первый слайд презентации
ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ НАЧЕРТЕТЕЛЬНОЙ ГЕОМЕТРИИ
Слайд 2
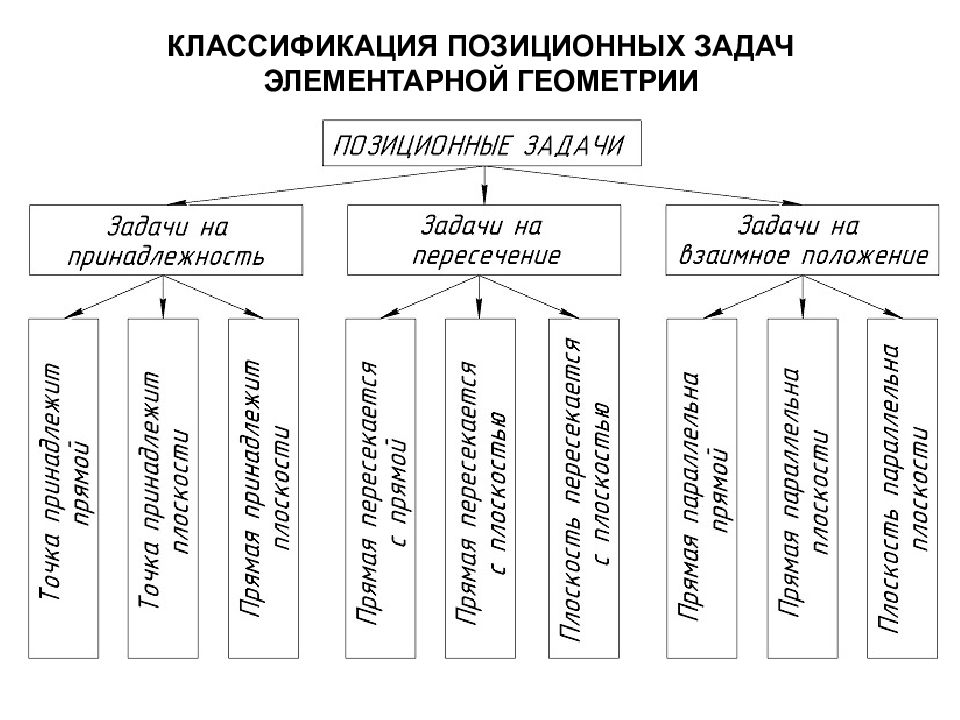
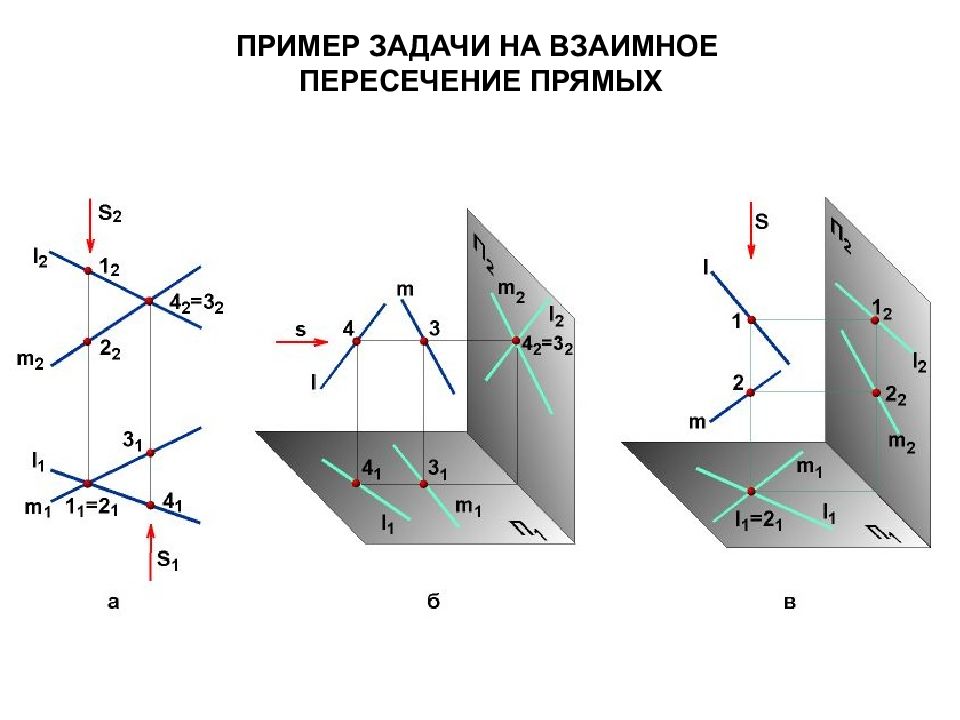
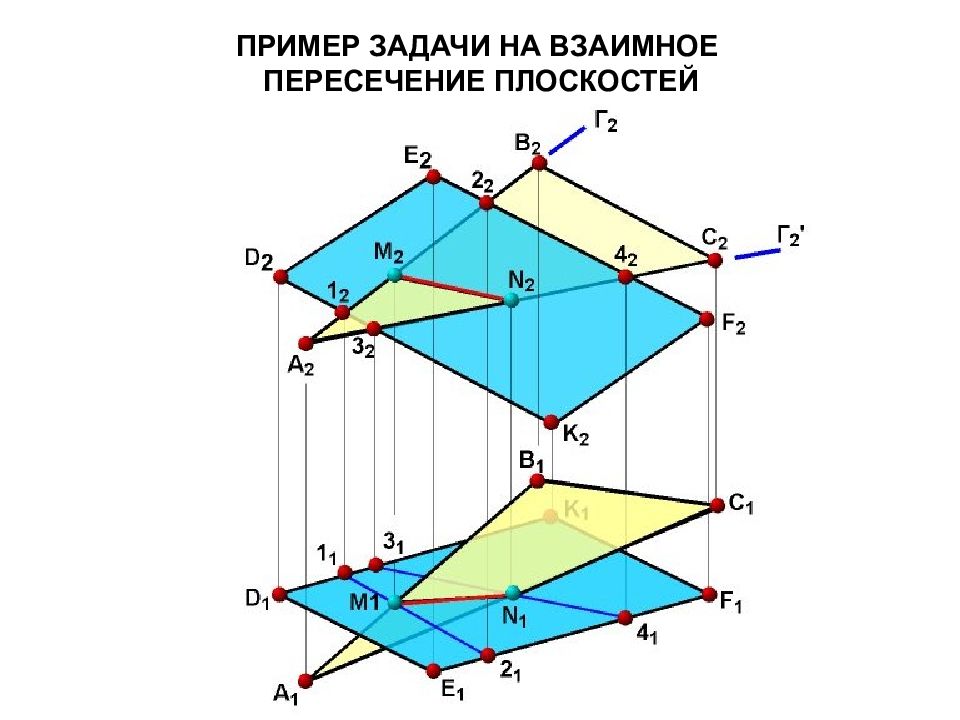
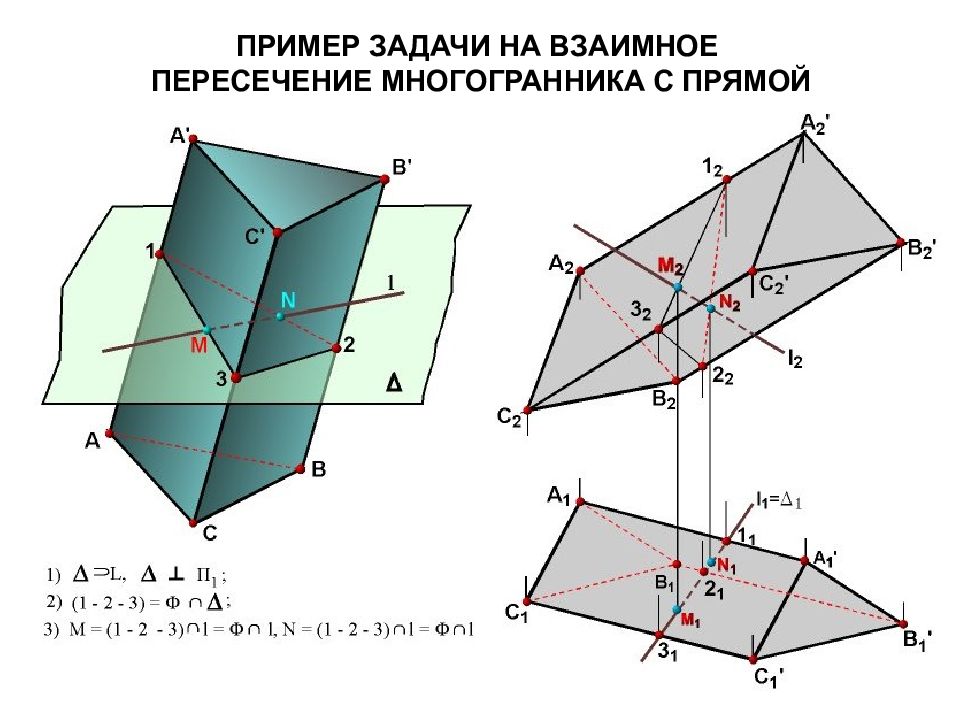
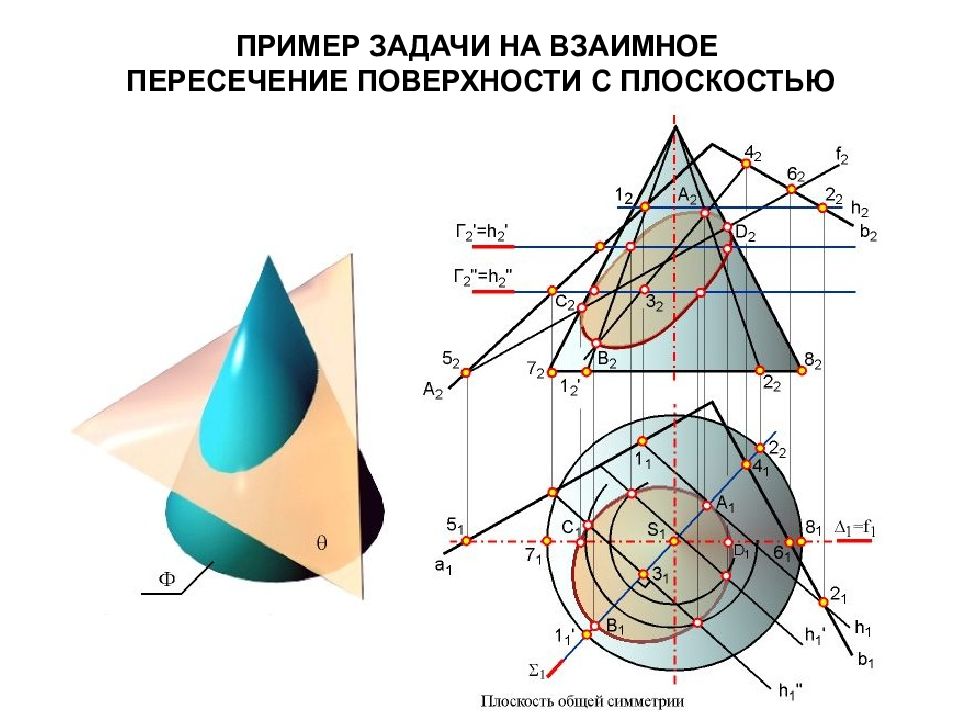
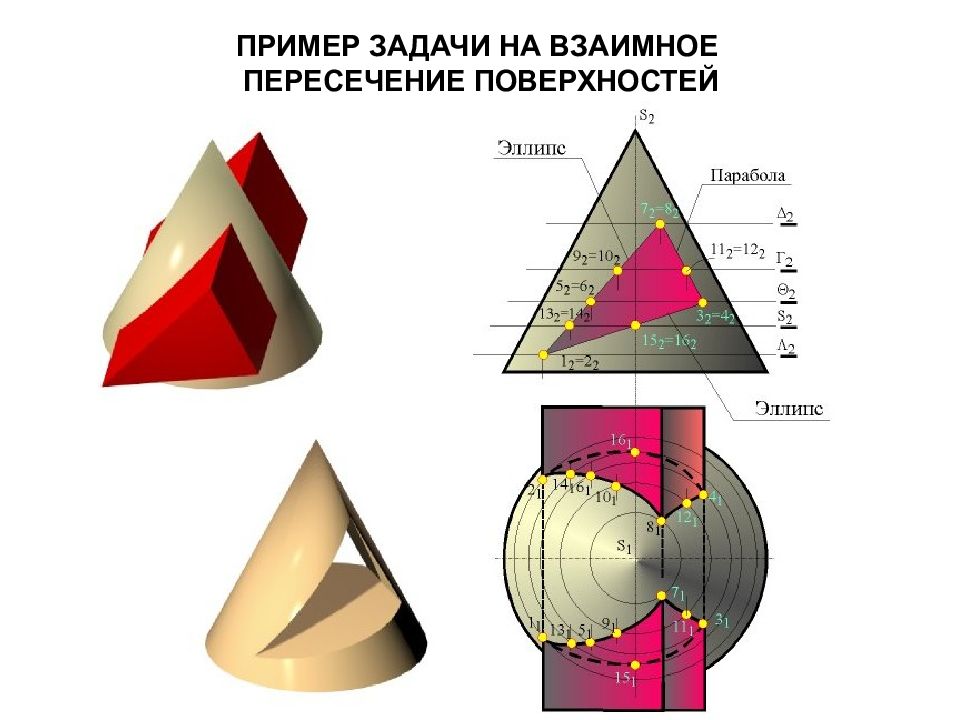
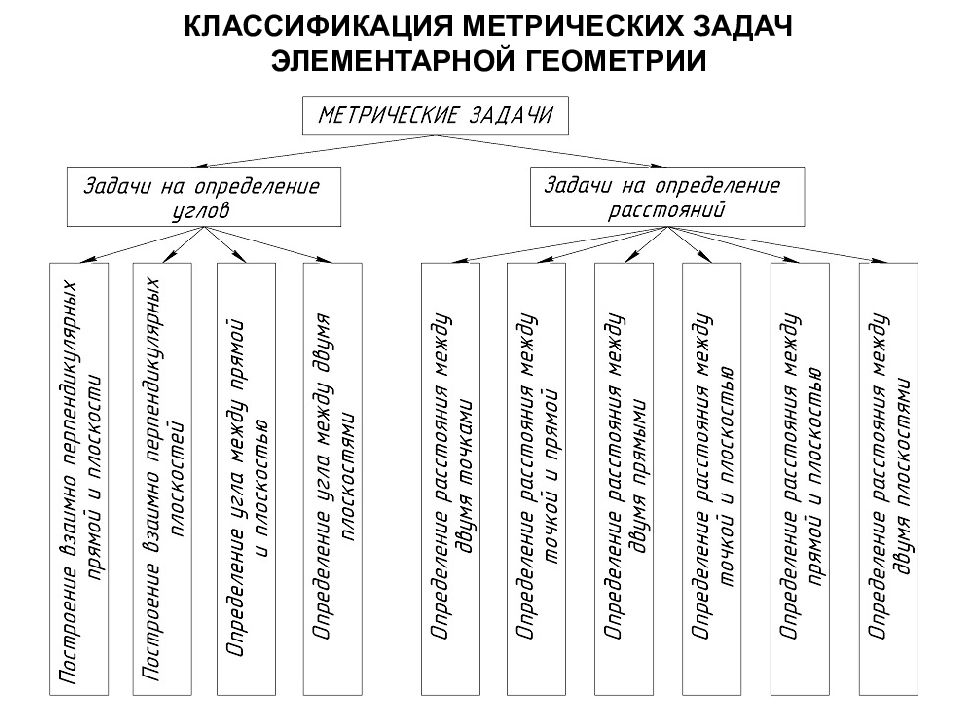
Позиционными задачами называются задачи на построение элементов, общих для взаимодействующих объектов, и задачи на взаимное положение геометрических объектов. Метрические задачи – это задачи на определение линейных или угловых размеров геометрических объектов, а также расстояний и углов между ними.
Слайд 11
Для решения метрических задач в инженерной графике используются способы преобразования проекций: способ вращения (вращение, совмещение, плоско-параллельное перемещение); - способ замены плоскостей проекций.
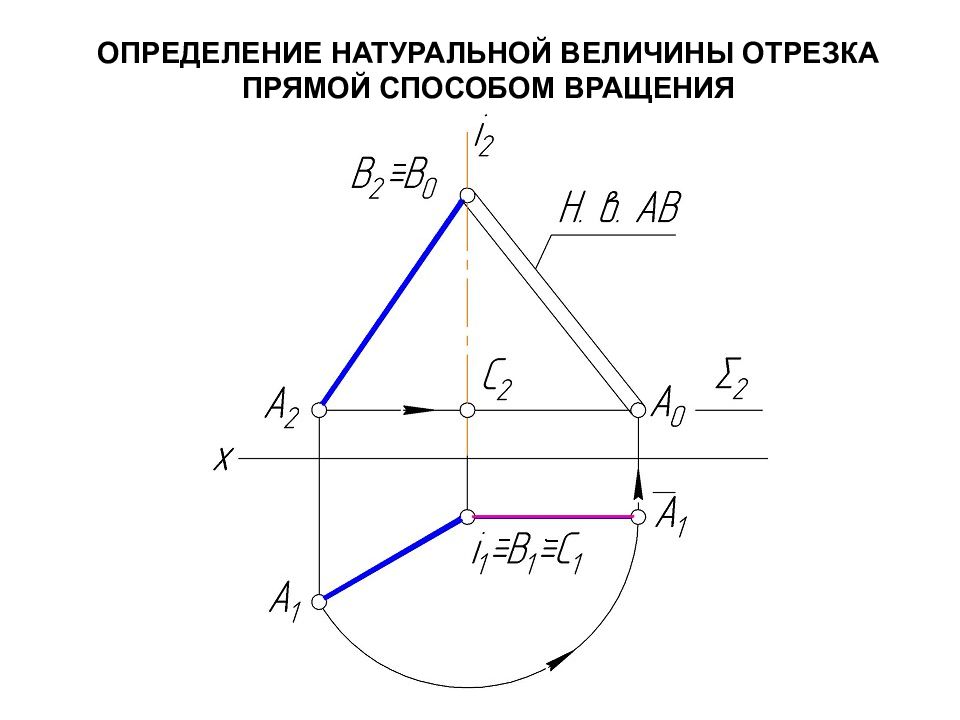
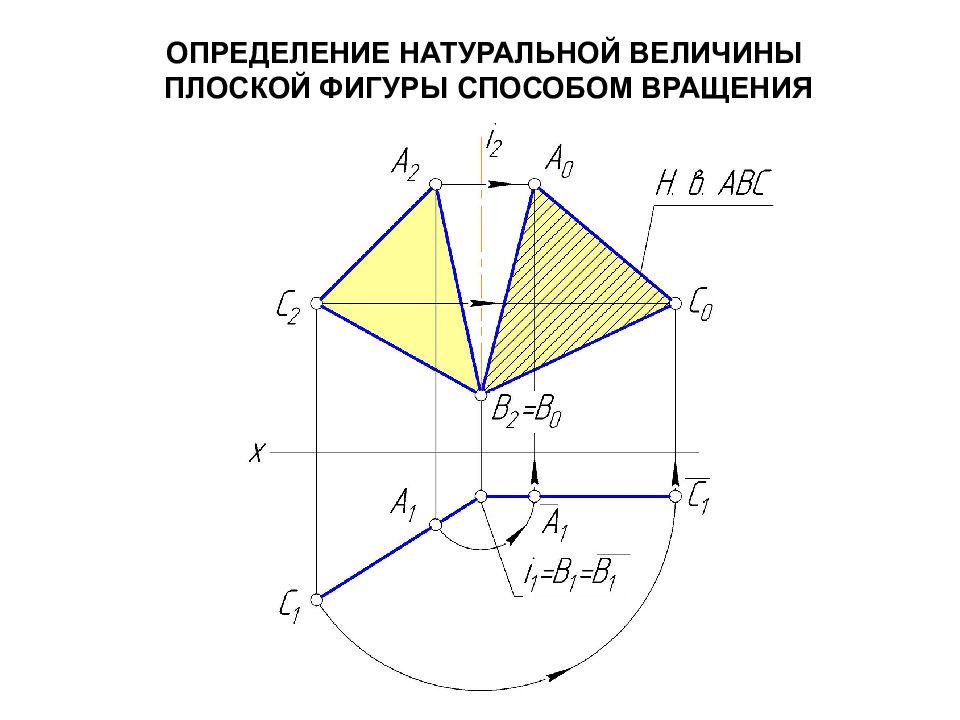
Слайд 12: СПОСОБ ВРАЩЕНИЯ
Способ вращения вокруг неподвижной оси используется для определения натуральной величины плоских фигур Элементы способа: а) ось вращения і – прямая, вокруг которой вращается точка. Ось вращения берут перпендикулярной к плоскостям проекций π 1 или π 2 ; б) плоскость вращения, т. е. плоскость, в которой точка перемещается и которая перпендикулярна к оси вращения; в) центр вращения – точка пересечения оси с плоскостью вращения; г) радиус вращения – расстояние от точки до центра вращения.
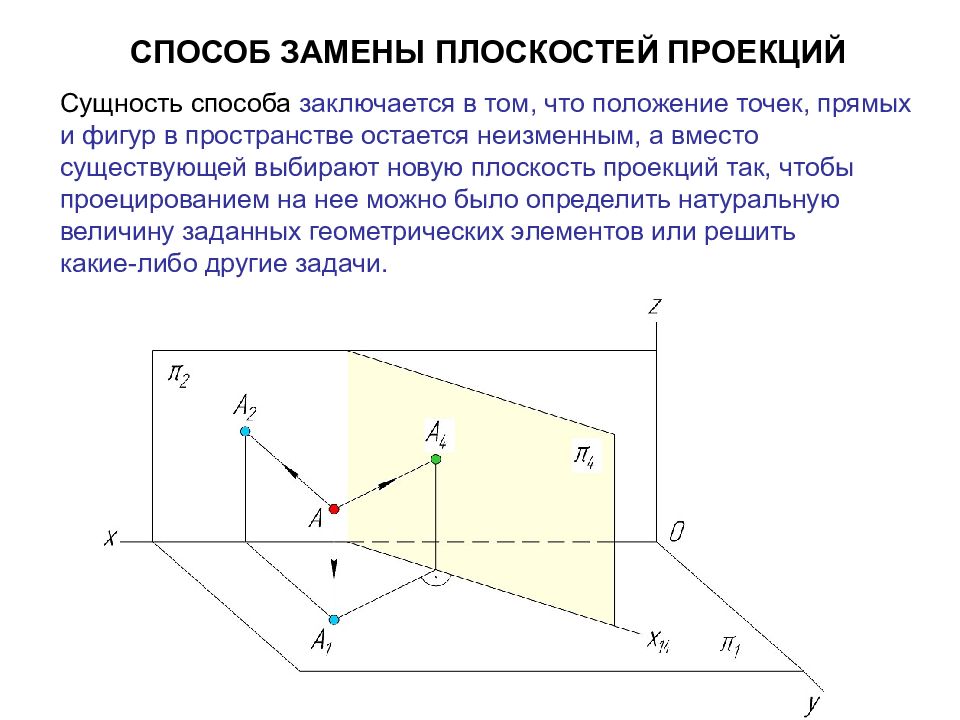
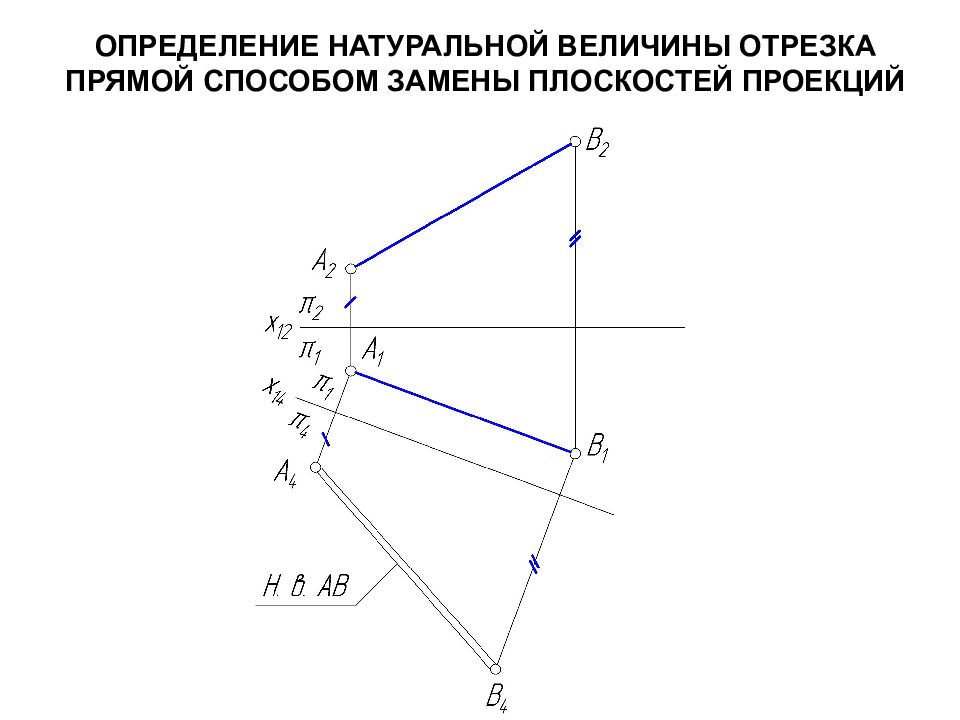
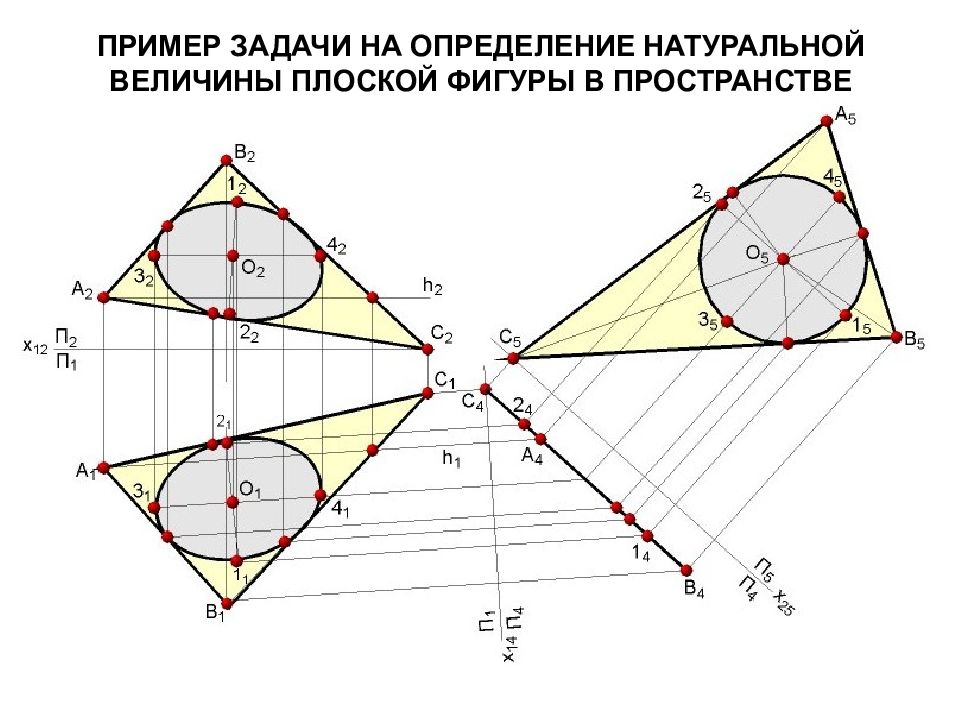
Слайд 15: СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Сущность способа заключается в том, что положение точек, прямых и фигур в пространстве остается неизменным, а вместо существующей выбирают новую плоскость проекций так, чтобы проецированием на нее можно было определить натуральную величину заданных геометрических элементов или решить какие-либо другие задачи.