Слайд 2: Развёртка поверхности
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга). Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся. Основные свойства развертки: длины двух соответствующих линий поверхности и ее развертки равны между собой; угол между линиями на поверхности равен углу между соответствующими им линиями на развертке; прямой на поверхности соответствует также прямая на развертке; параллельным прямым на поверхности соответствуют также параллельные прямые на развертке; если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.
Слайд 3: РАЗВЕРТКА ПОВЕРХНОСТИ МНОГОГРАННИКОВ
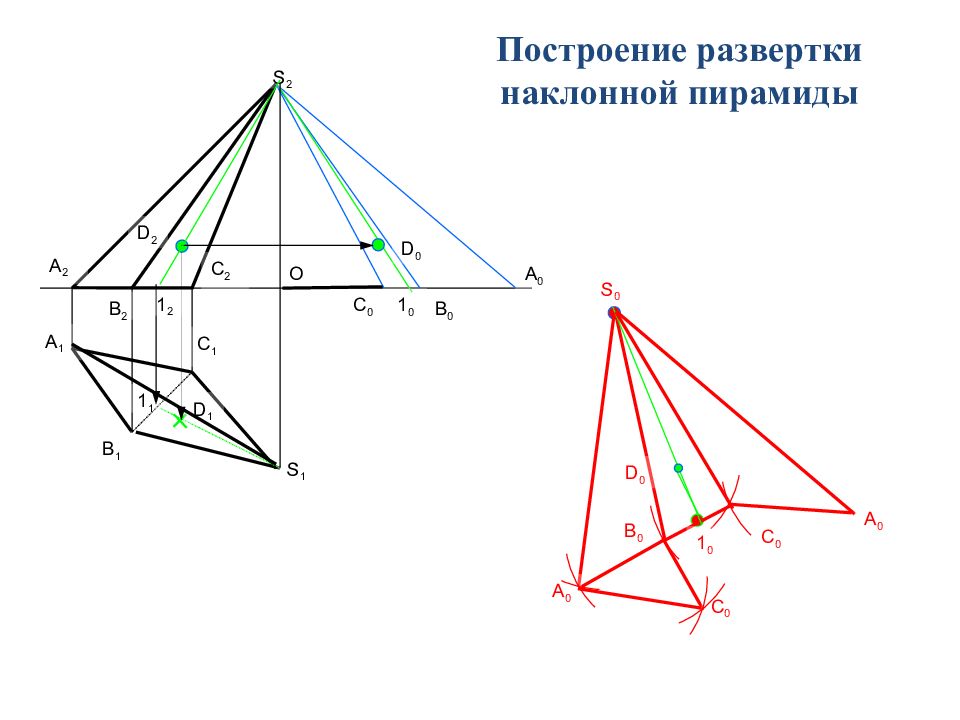
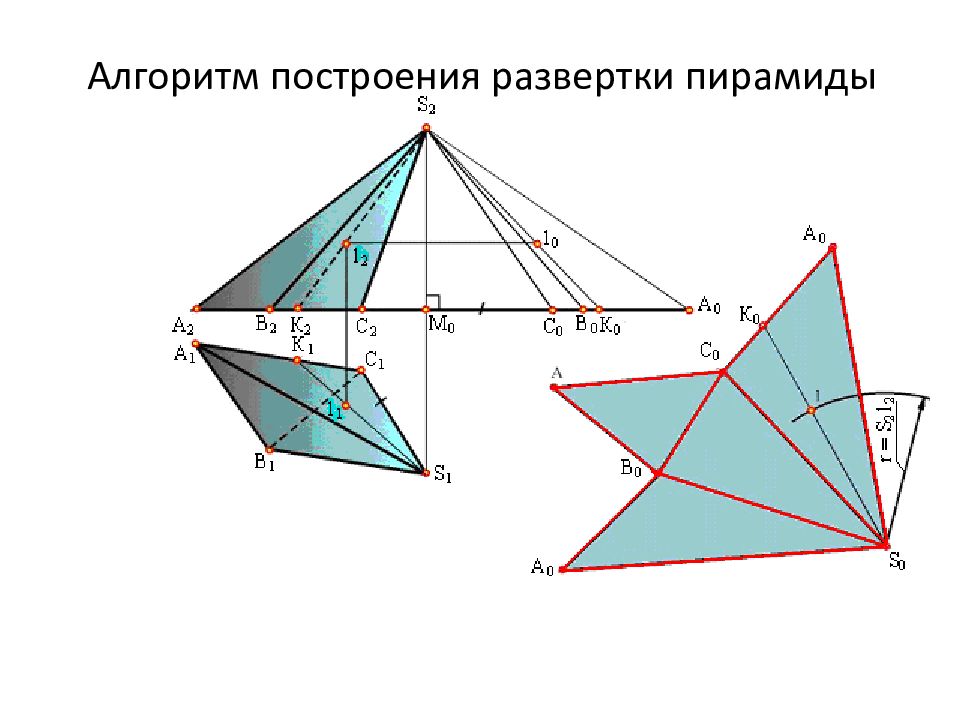
Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью. а) Пирамида и ее развертка. Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников. Существует три метода построения развертки многогранных поверхностей: 1. Метод треугольника. 2. Метод нормального сечения. 3. Метод раскатки. Рассмотрим применение каждого метода на примерах развертки пирамиды (метод треугольника) и призмы (метод нормального сечения и раскатки)
Слайд 4
А 1 А 2 D 2 D 1 B 1 C 2 C 1 S 1 S 2 1 1 A 0 C 0 B 0 1 0 D 0 O B 2 1 2 S 0 A 0 C 0 B 0 A 0 С 0 1 0 D 0 Построение развертки наклонной пирамиды
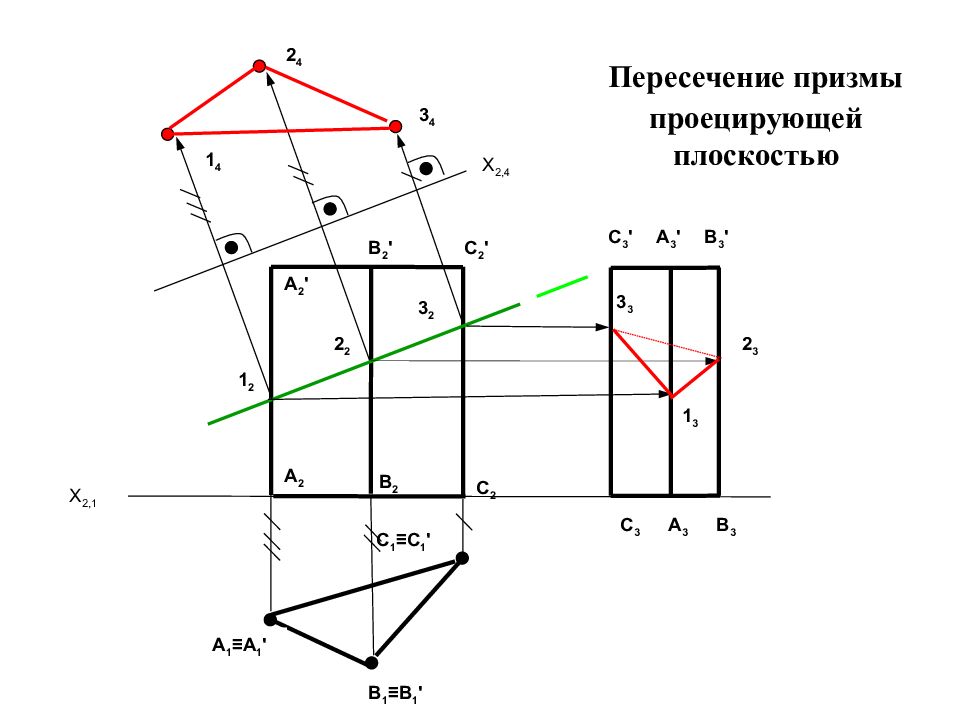
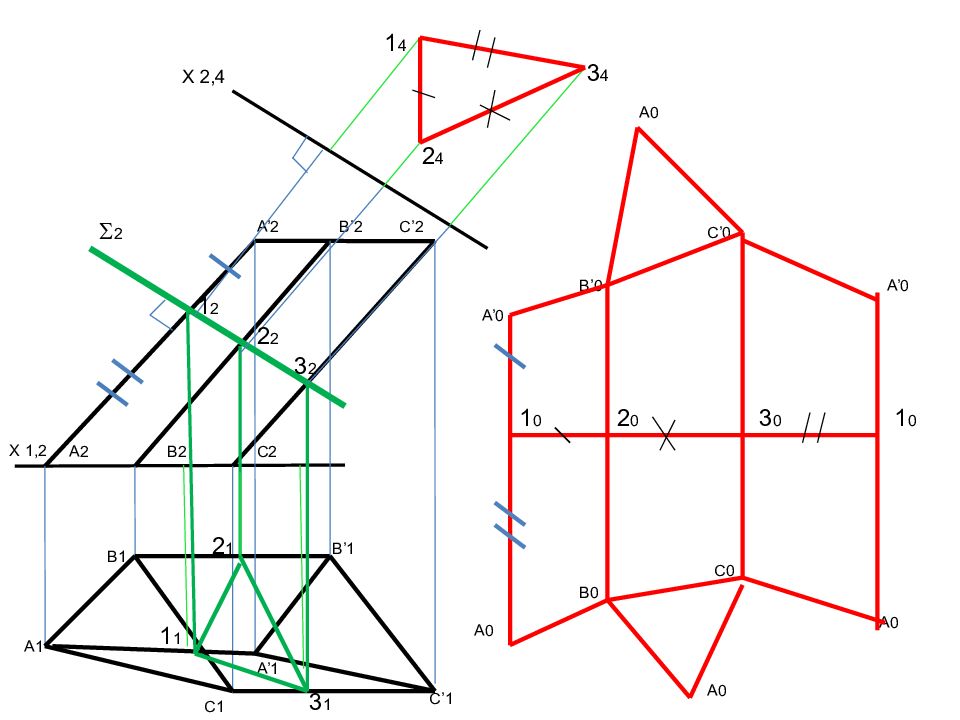
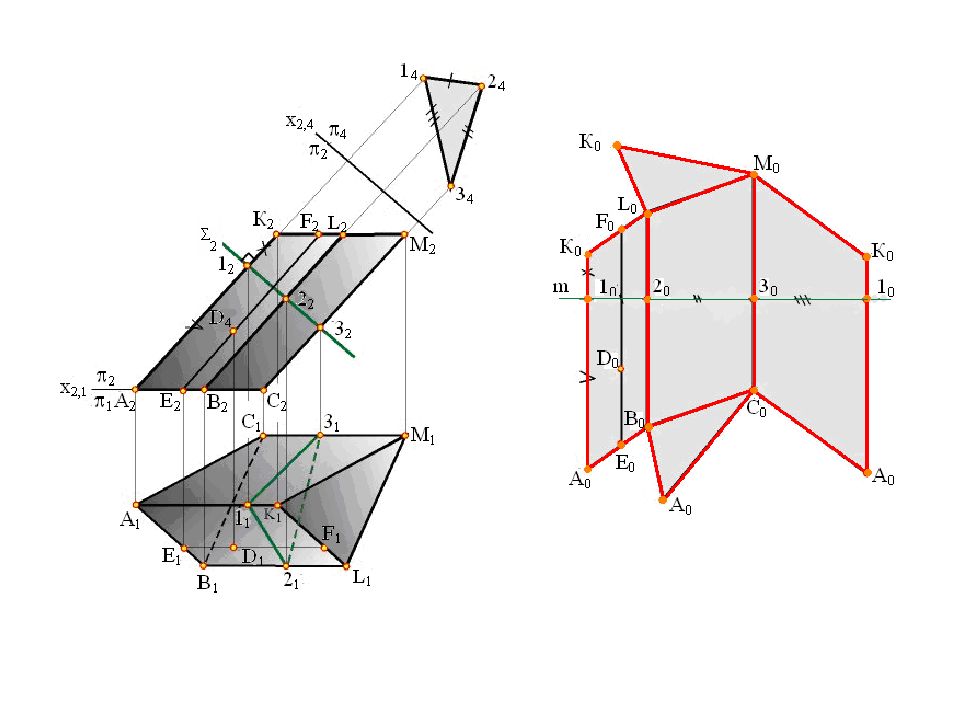
X 2,1 А 1 ≡А 1 ' В 1 ≡В 1 ' С 1 ≡С 1 ' С 2 В 2 ' В 2 А 2 А 2 ' С 2 ' В 3 ' С 3 ' А 3 ' А 3 В 3 С 3 1 2 2 2 3 2 3 3 2 3 1 3 X 2,4 3 4 2 4 1 4 Пересечение призмы проецирующей плоскостью
Слайд 7
Х 1,2 А2 В2 С2 А ’ 2 B’ 2 C’ 2 А 1 B1 C1 А ’1 B’1 C’1 2 1 2 2 2 3 2 1 1 2 1 3 1 X 2,4 1 4 2 4 3 4 1 0 2 0 3 0 1 0 А ’ 0 А0 В ’ 0 В 0 C’ 0 C 0 А0 А ’ 0 А0 А0
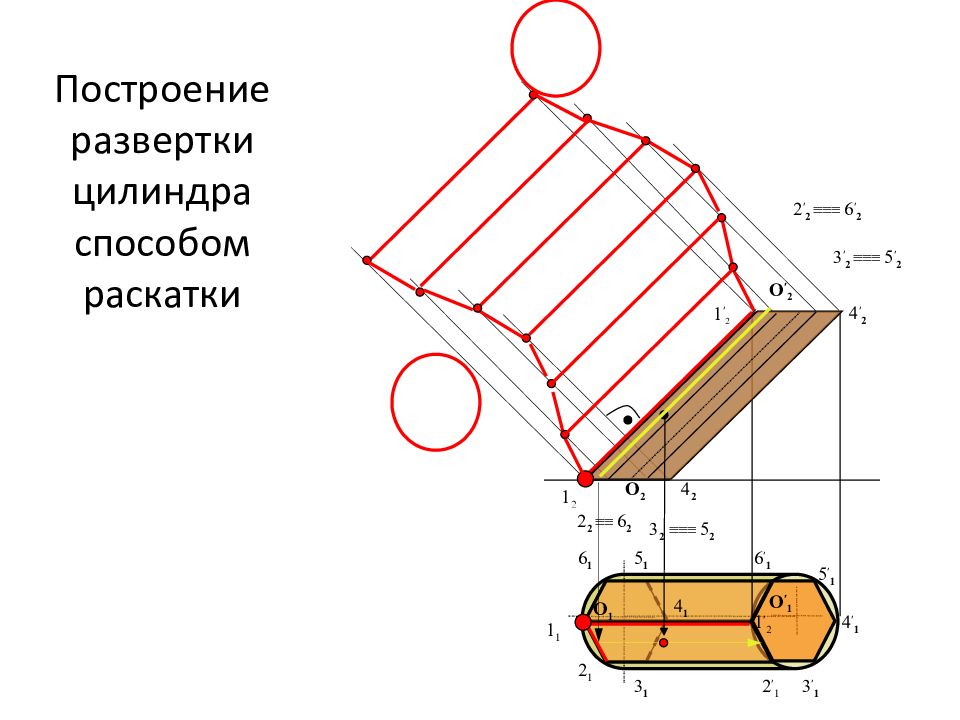
Слайд 9: Построение развертки цилиндра способом раскатки
1 2 4 2 1 ′ 2 4 ′ 2 1 1 2 1 3 1 4 1 5 1 6 1 2 ′ 1 1 ′ 2 3 ′ 1 4 ′ 1 5 ′ 1 6 ′ 1 O 2 O ′ 1 O ′ 2 O 1 2 2 ≡≡ 6 2 3 2 ≡≡≡ 5 2 2 ′ 2 ≡≡≡ 6 ′ 2 3 ′ 2 ≡≡≡ 5 ′ 2 Построение развертки цилиндра способом раскатки
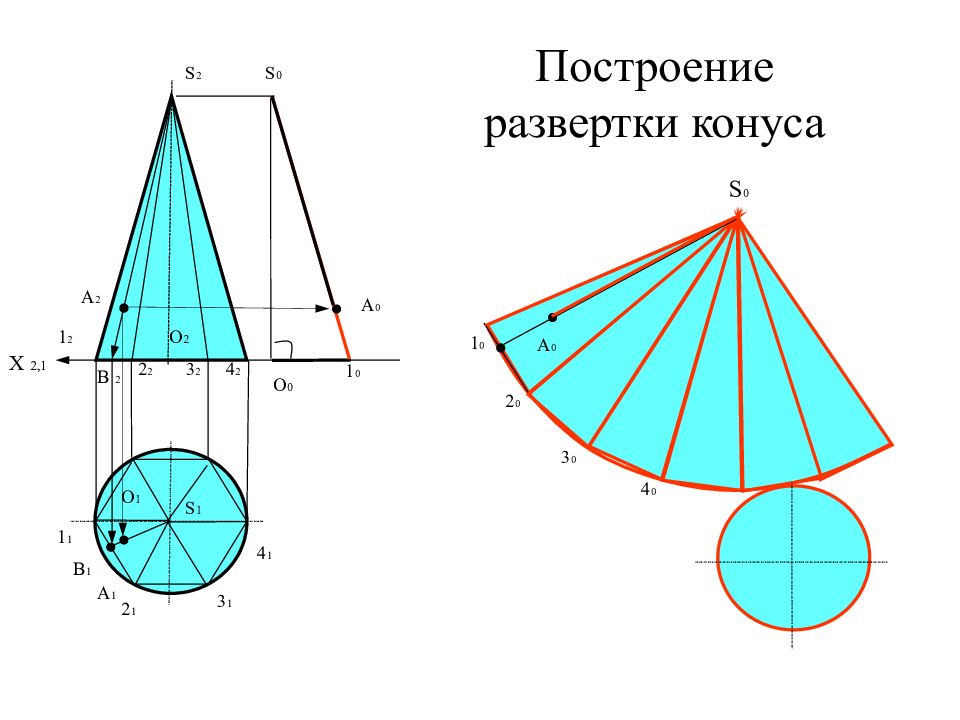
Слайд 10: Построение развертки конуса
S 2 S 1 S 0 1 2 1 1 1 0 2 2 2 1 2 0 3 2 3 1 3 0 4 2 4 1 4 0 S 0 1 0 О 0 А 2 B 2 B 1 А 1 А 0 А 0 X 2,1 О 2 О 1
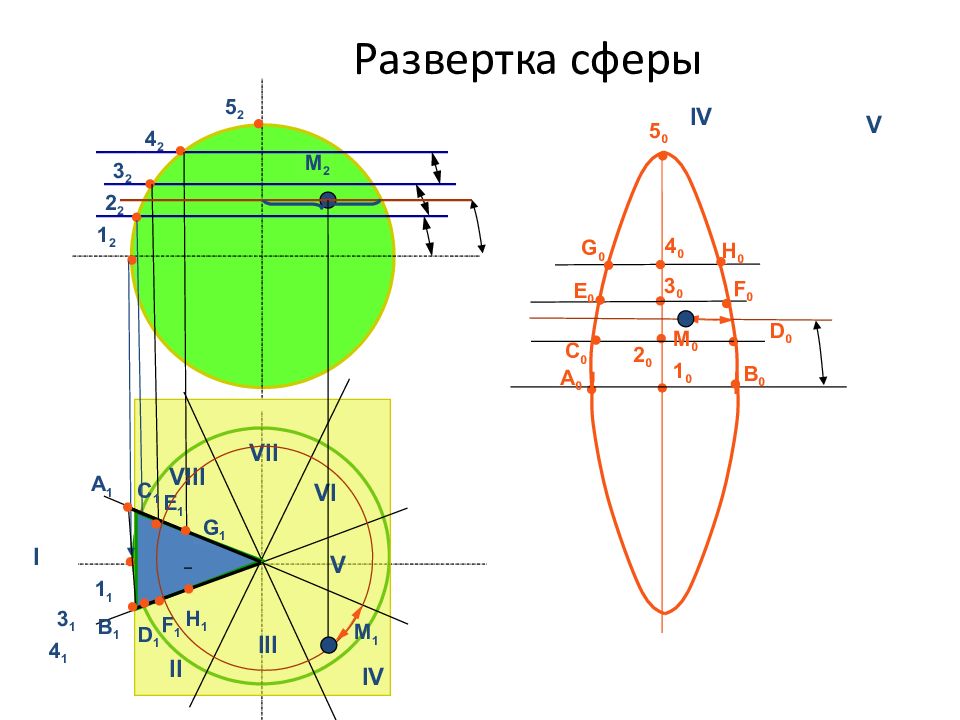
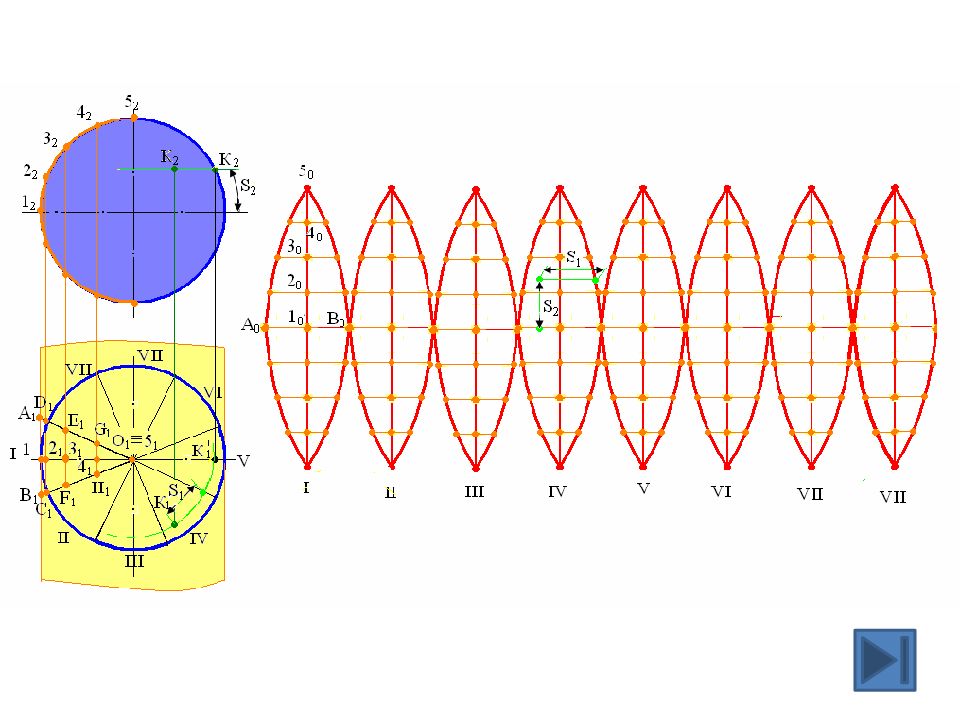
Слайд 11: Развертка сферы
I II III IV V VI VII VIII 2 2 3 2 4 2 5 2 1 2 1 1 2 1 3 1 4 1 А 1 В 1 C 1 D 1 1 0 2 0 3 0 4 0 5 0 C 0 D 0 E 0 F 0 E 1 F 1 A 0 B 0 G 1 H 1 G 0 H 0 M 2 M 1 IV V M 0