Первый слайд презентации: Тема урока: Компланарные векторы. Правило параллелепипеда
Слайд 2: Цели урока:
- усвоить определение компланарных векторов; - рассмотреть признак компланарности трёх векторов; - рассмотреть правило параллелепипеда сложения трёх некомпланарных векторов; - научиться применять полученные знания при решении задач.
Слайд 3: Определение
Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости. Иначе: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
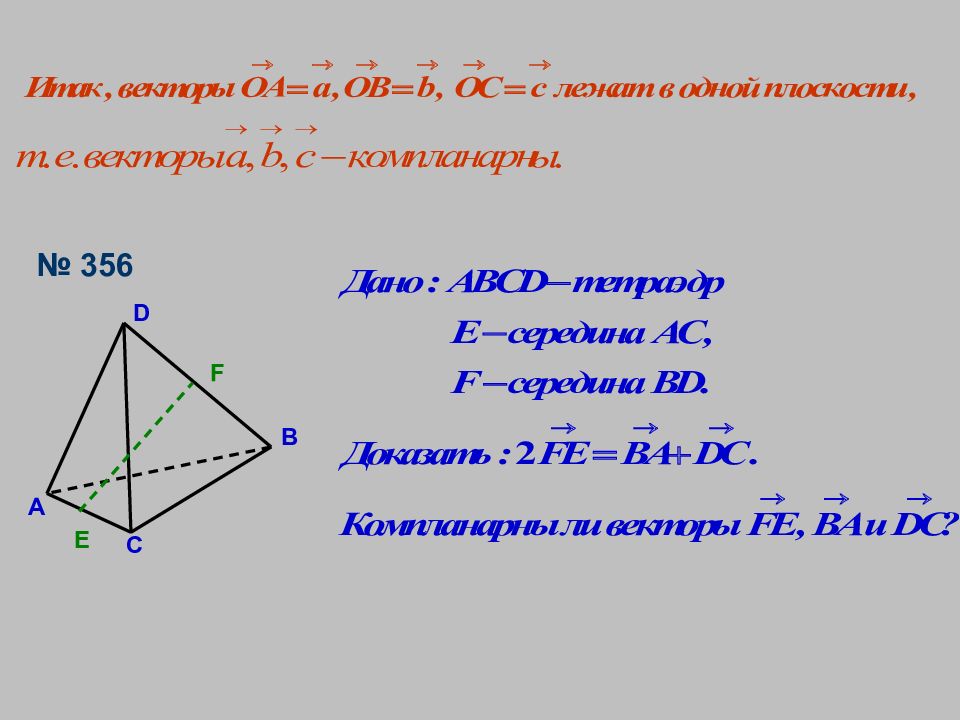
Слайд 5: Признак компланарности трёх векторов
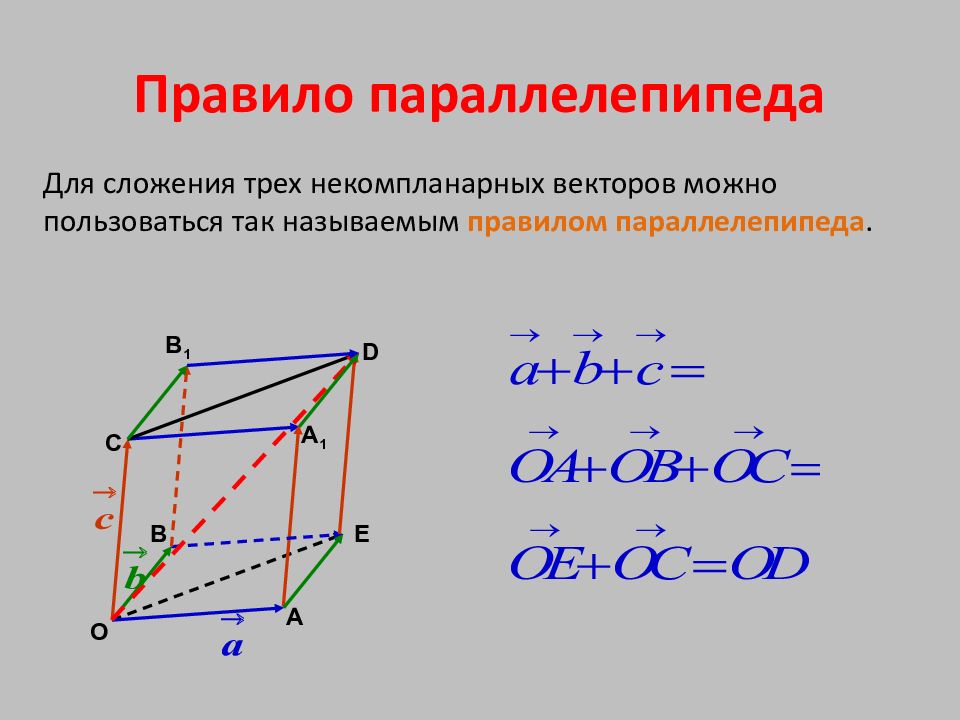
Слайд 8: Правило параллелепипеда
Для сложения трех некомпланарных векторов можно пользоваться так называемым правилом параллелепипеда. Е С В А О D B 1 A 1
Слайд 11: Цели урока
- изучить теорему о разложении вектора по трём некомпланарным векторам; - научиться применять полученные знания при решении задач.
Слайд 12
Если вектор представлен в виде: где x, y, z – некоторые числа, то говорят, что вектор разложен по векторам, и. Числа x, y, z называются коэффициентами разложения. ОПРЕДЕЛЕНИЕ
Слайд 13
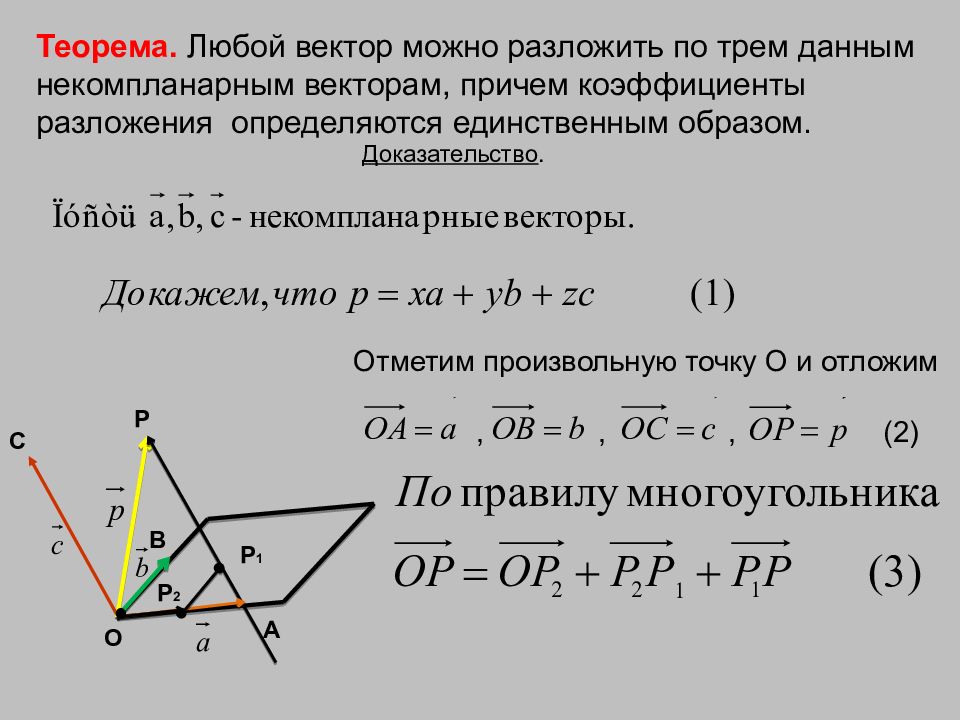
С В А О P Теорема. Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом. Доказательство. Отметим произвольную точку О и отложим ,,, (2) P 1 P 2
Слайд 14
Векторы коллинеарны, поэтому существуют числа х, у, z такие, что. С В А О P P 1 P 2 х-х 1 =0, у- y 1 =0, z -z 1 =0 Предположим, что z -z 1 0 х = х 1, у =y 1, z =z 1 Подставив эти выражения, получим