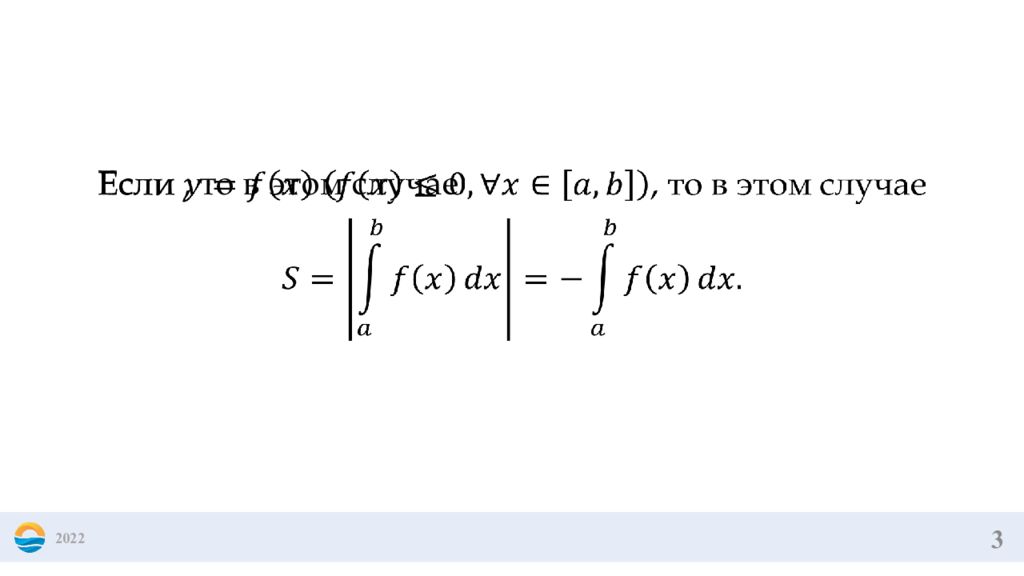2022 ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
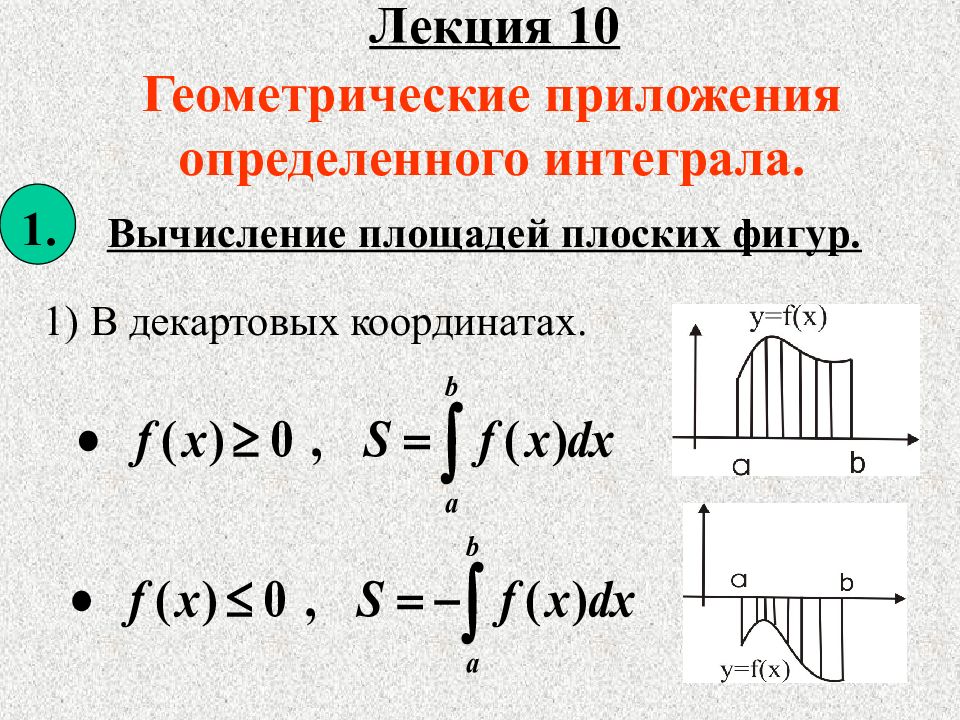
2 2022 ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР Если непрерывная кривая задана в прямоугольных координатах уравнением, то площадь плоской фигуры, ограниченной этой кривой, прямыми и осью, вычисляется по формуле
3 2022 Если, то в этом случае
4 2022 Площадь криволинейной трапеции, ограниченной прямыми, непрерывной кривой и осью, вычисляется по формуле
5 2022 Если криволинейная трапеция ограничена кривыми , то ее площадь равна
6 2022 Площадь криволинейной трапеции, ограниченной прямыми, осью и кривой, заданной параметрическими уравнениями, находится по формуле при условии, что строго возрастает на. Если же строго убывающая на функция, то
7 2022 Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой осью и прямыми, вокруг оси, находится по формуле ВЫЧ И СЛЕНИЕ ОБЪЕМА ТЕЛА ВРАЩЕНИЯ
8 2022 Если вокруг оси вращается фигура, ограниченная кривыми и прямыми, то объем тела вращения вычисляется по формуле
9 2022 Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой осью и прямыми, вокруг оси, находится по формуле
10 2022 Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой заданной параметрическими уравнениями осью и прямыми, вокруг оси, находится по формуле
11 2022 ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ КРИВОЙ Если дуга кривой задана уравнением и функция имеет непрерывную производную в промежутке, то длина дуги кривой, содержащейся между двумя точками с абсциссами, вычисляется по формуле
12 2022 Если дуга кривой задана уравнением и функция имеет непрерывную производную в промежутке, то длина дуги кривой, содержащейся между двумя точками с ординат, вычисляется по формуле
13 2022 Длина дуги кривой, заданной параметрически, – непрерывно дифференцируемые функции, выражается формулой
2022 Спасибо за внимание! МАТЕМАТИЧЕСКИЙ АНАЛИЗ И ЛИНЕЙНАЯ АЛГЕБРА БФУ имени И. Канта
