у х
1 задание 2 задание*
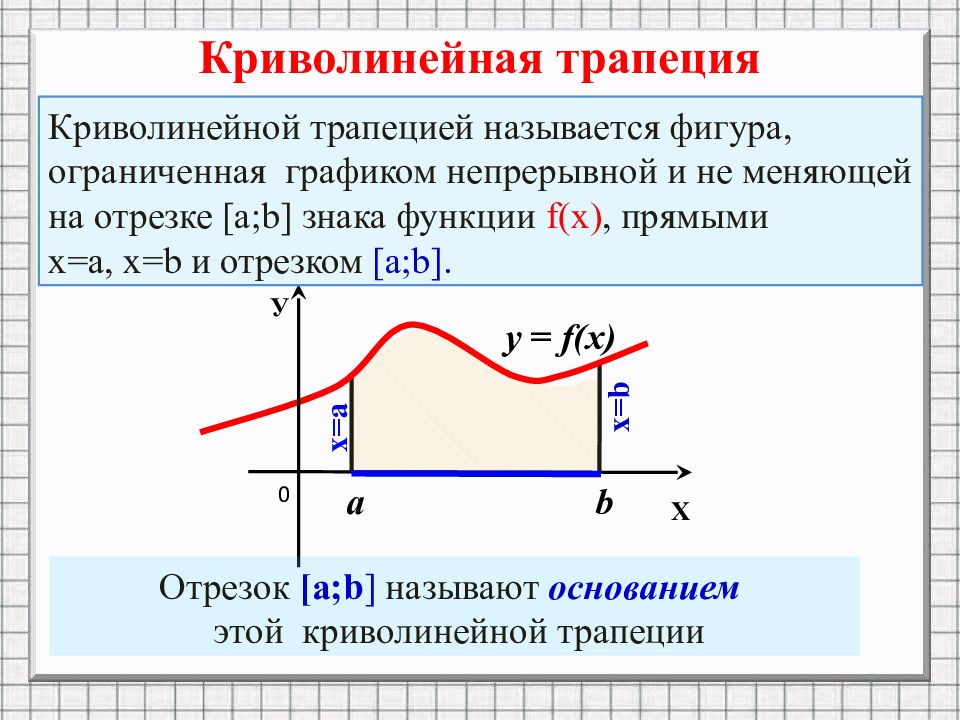
a b х=а x=b 0 y = f(x) Х У Криволинейная трапеция Отрезок [ a;b ] называют основанием этой криволинейной трапеции Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [ а;b ] знака функции f ( х ), прямыми х=а, x=b и отрезком [ а;b ].
Криволинейная трапеция 0 2 0 0 0 1 -1 -1 2 -1 -2 У=х²+2х У=0,5х+1
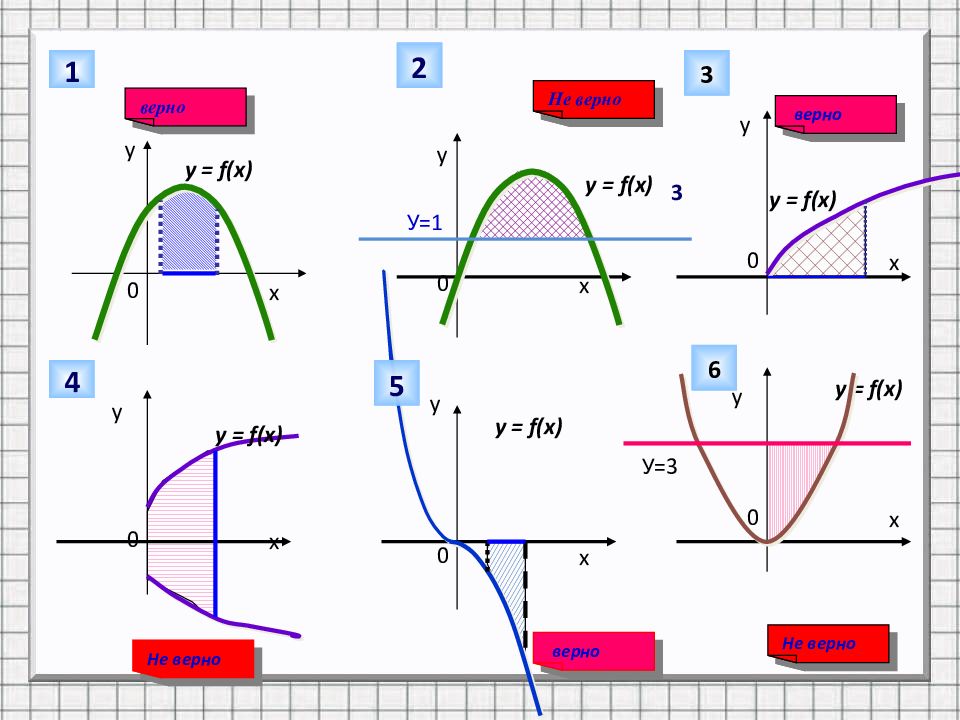
Какие из заштрихованных на рисунке фигур являются криволинейными трапециями, а какие нет? Заполнить таблицу №1 Да/нет №2 №3 №4 №5 №6
0 х у 1 Не верно 0 х 0 х 0 х 0 х 0 х у у у у у У=1 2 верно 3 3 y = f(x ) y = f(x ) y = f(x ) y = f(x ) y = f(x ) y = f(x ) У=3 4 5 6 Не верно Не верно верно верно
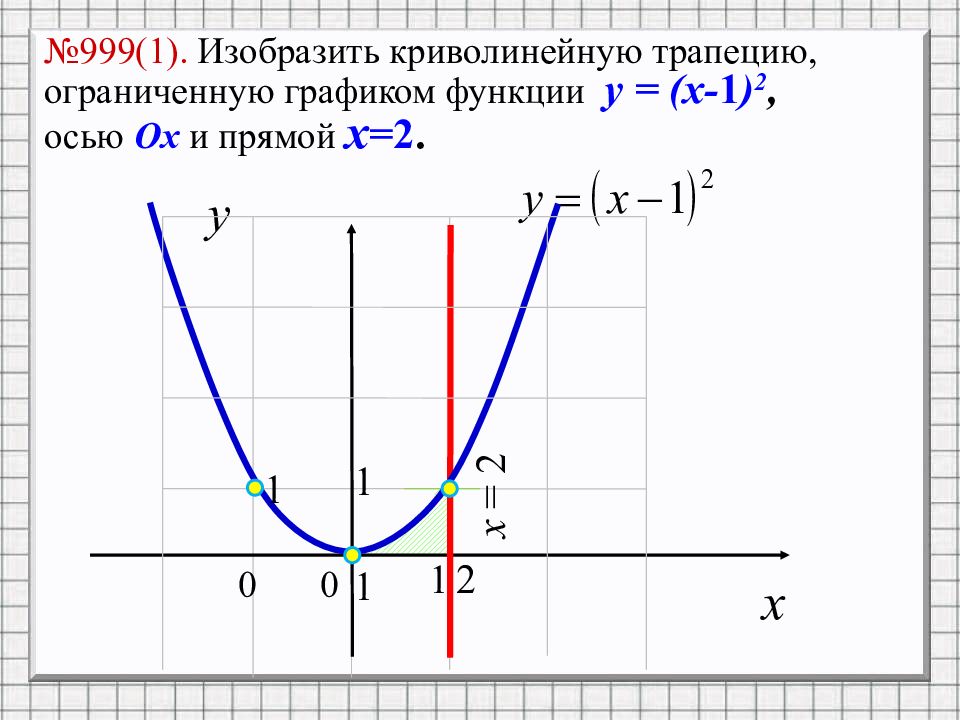
x = 2
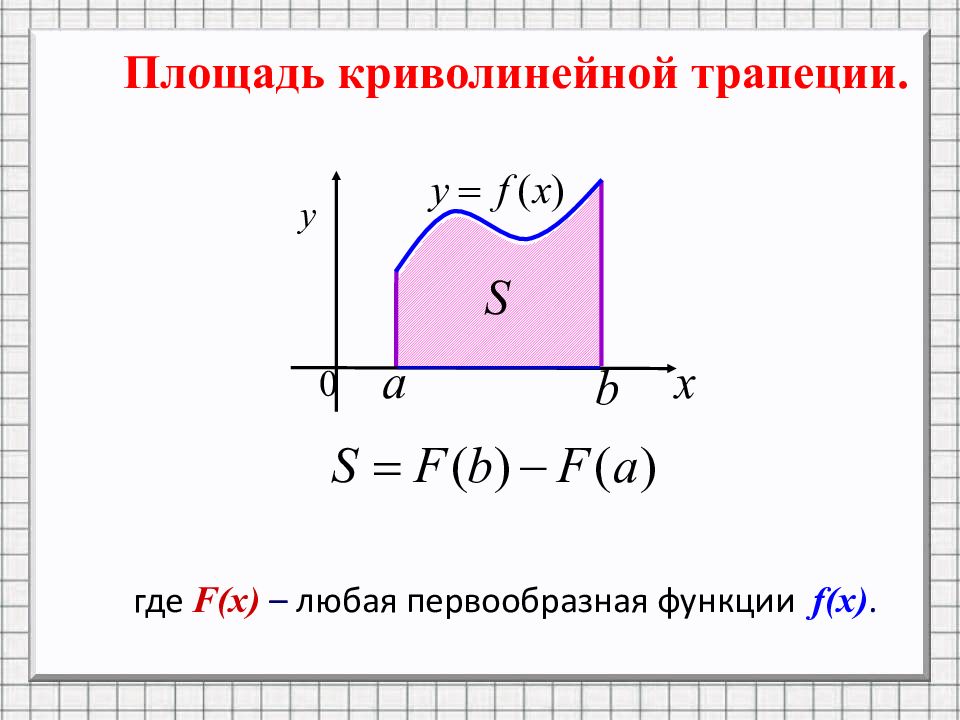
Площадь криволинейной трапеции. где F(x) – любая первообразная функции f(x).
Формула Ньютона-Лейбница 1643—1727 1646—1716
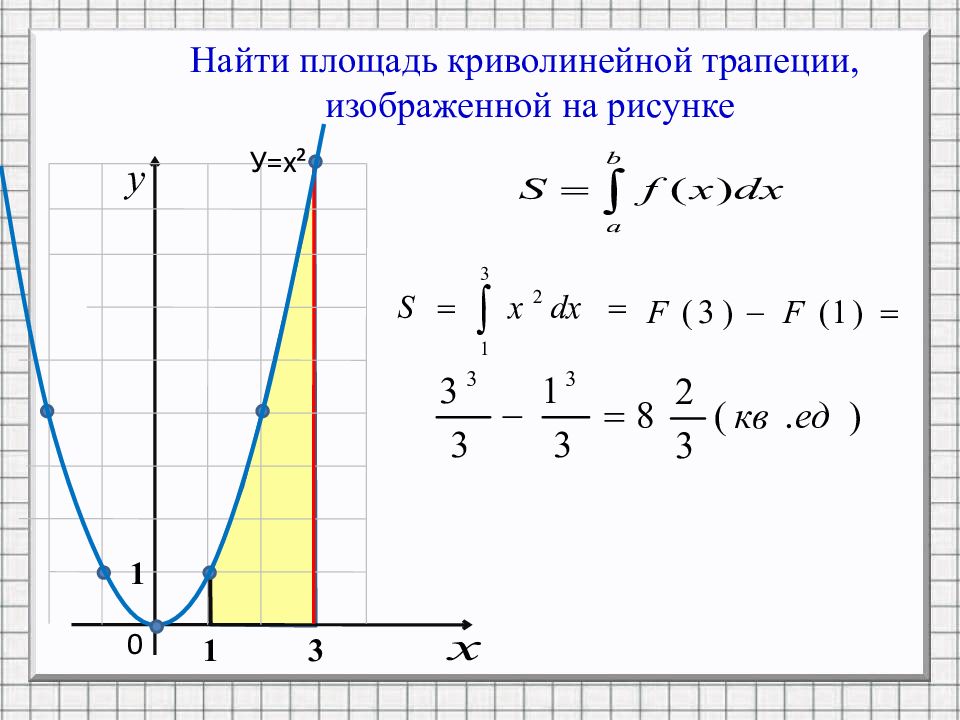
Найти площадь криволинейной трапеции, изображенной на рисунке 0 1 3 У=х ² 1
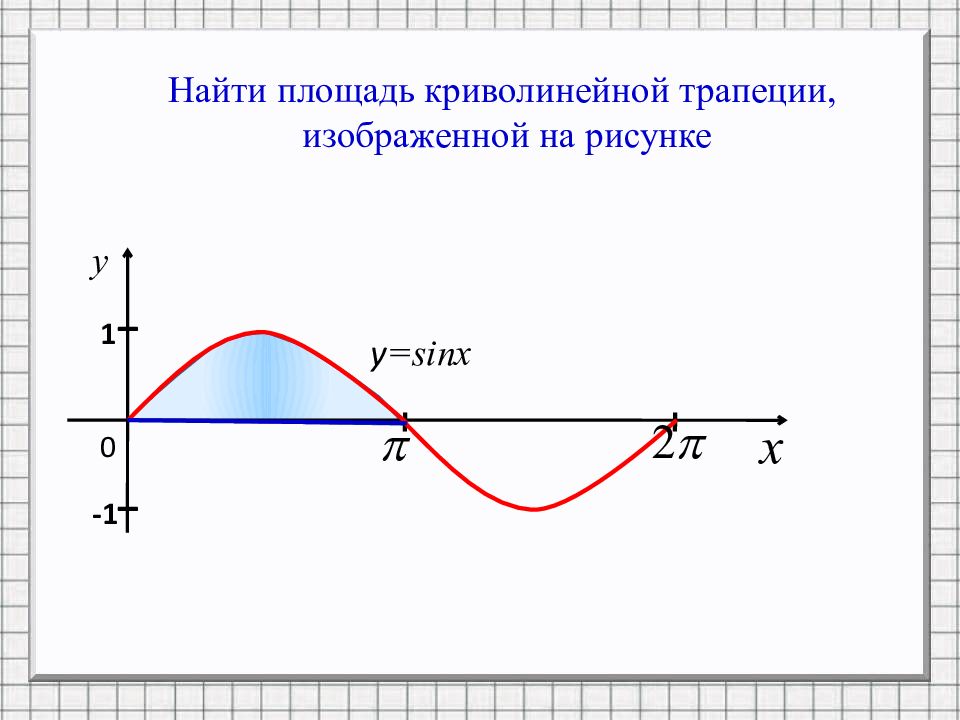
Найти площадь криволинейной трапеции, изображенной на рисунке 0 y = sinx I I 1 -1
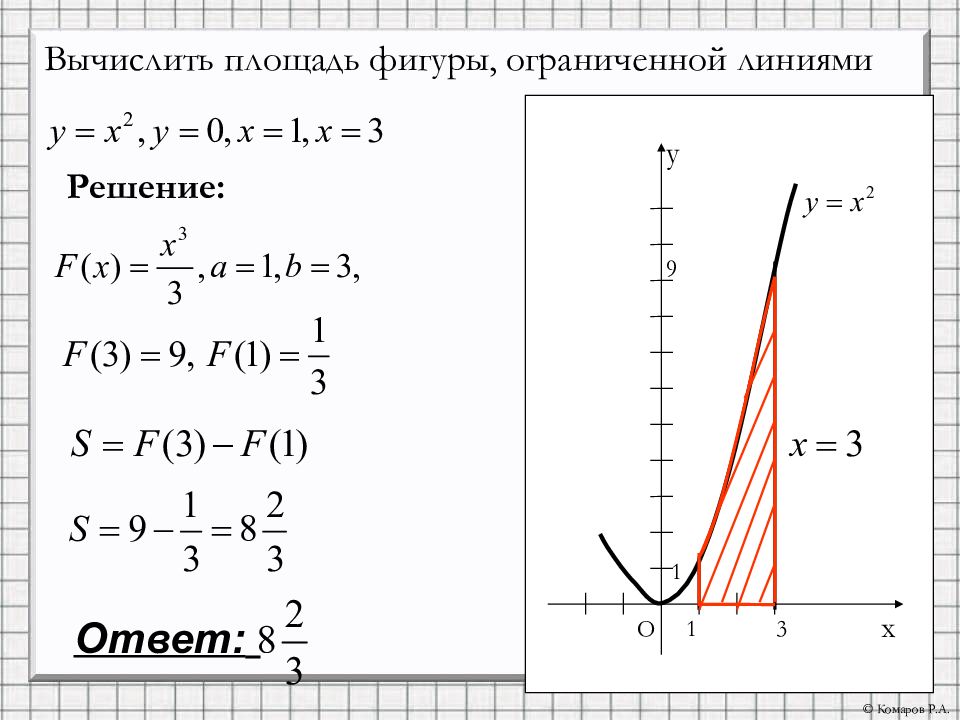
х О у 1 3 1 9 Вычислить площадь фигуры, ограниченной линиями Решение: Ответ: © Комаров Р.А.
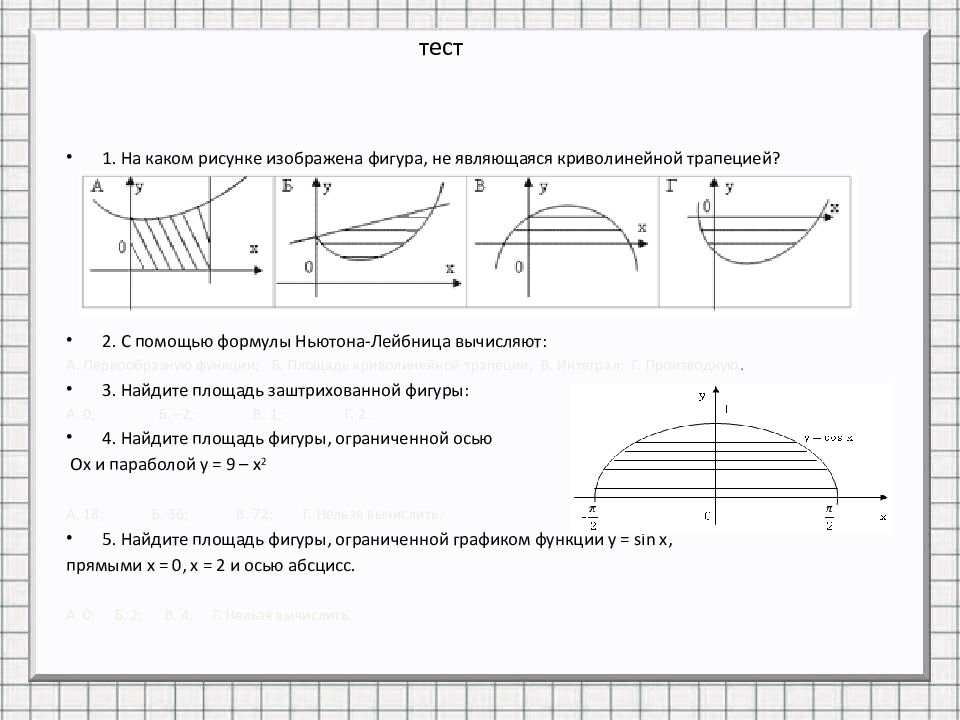
1. На каком рисунке изображена фигура, не являющаяся криволинейной трапецией? 2. С помощью формулы Ньютона-Лейбница вычисляют: А. Первообразную функции; Б. Площадь криволинейной трапеции; В. Интеграл; Г. Производную. 3. Найдите площадь заштрихованной фигуры: А. 0; Б. –2; В. 1; Г. 2. 4. Найдите площадь фигуры, ограниченной осью Ох и параболой у = 9 – х 2 А. 18; Б. 36; В. 72; Г. Нельзя вычислить. 5. Найдите площадь фигуры, ограниченной графиком функции у = sin x, прямыми х = 0, х = 2 и осью абсцисс. А. 0; Б. 2; В. 4; Г. Нельзя вычислить.
1. Б; Г 2. Б,В; 3. Г; 4. Б; 5. В.
1. При каких значениях а площадь фигуры, ограниченной линиями у = х 2, у = 0, х = а, равна 9?
