«Определённый интеграл. Вычисление площади криволинейной трапеции»
Задача 1. В декартовой прямоугольной системе координат х0у дана фигура, ограниченная осью 0х, прямыми х=а, х= b (а< b ) и графиком непрерывной и неотрицательной на отрезке [ а; b ] функции y=f(x) ; назовём эту фигуру криволинейной трапецией. Требуется вычислить площадь криволинейной трапеции.
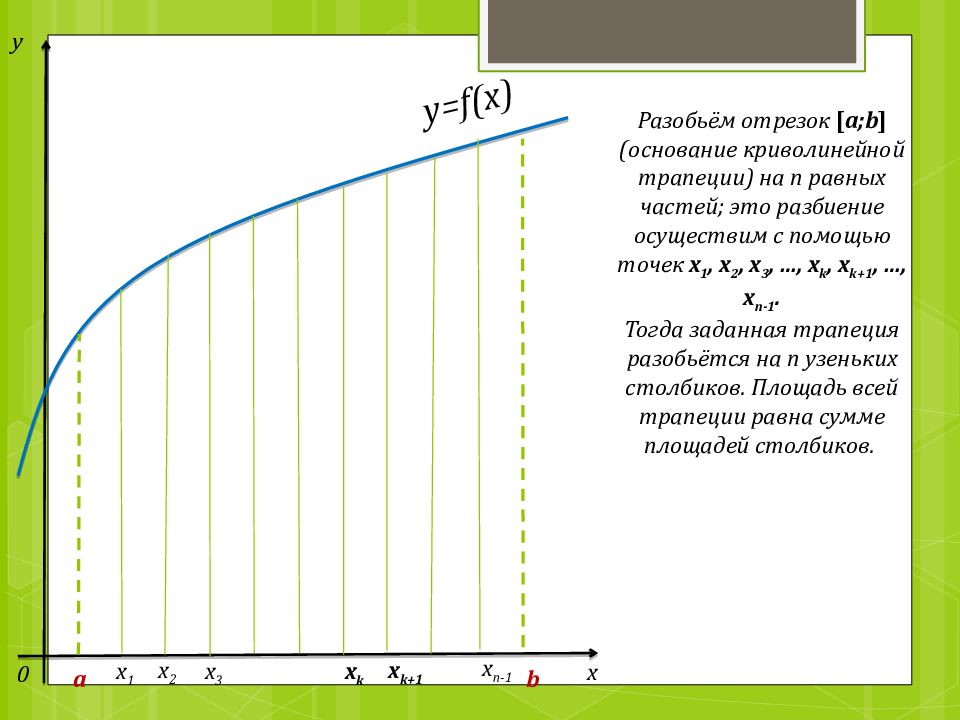
у х 0 y=f(x) x 1 x 2 x 3 х n -1 x k x k+1 a b Разобьём отрезок [ а; b ] (основание криволинейной трапеции) на n равных частей; это разбиение осуществим с помощью точек х 1, х 2, х 3, …, x k, x k+1, …, x n-1. Тогда заданная трапеция разобьётся на n узеньких столбиков. Площадь всей трапеции равна сумме площадей столбиков.
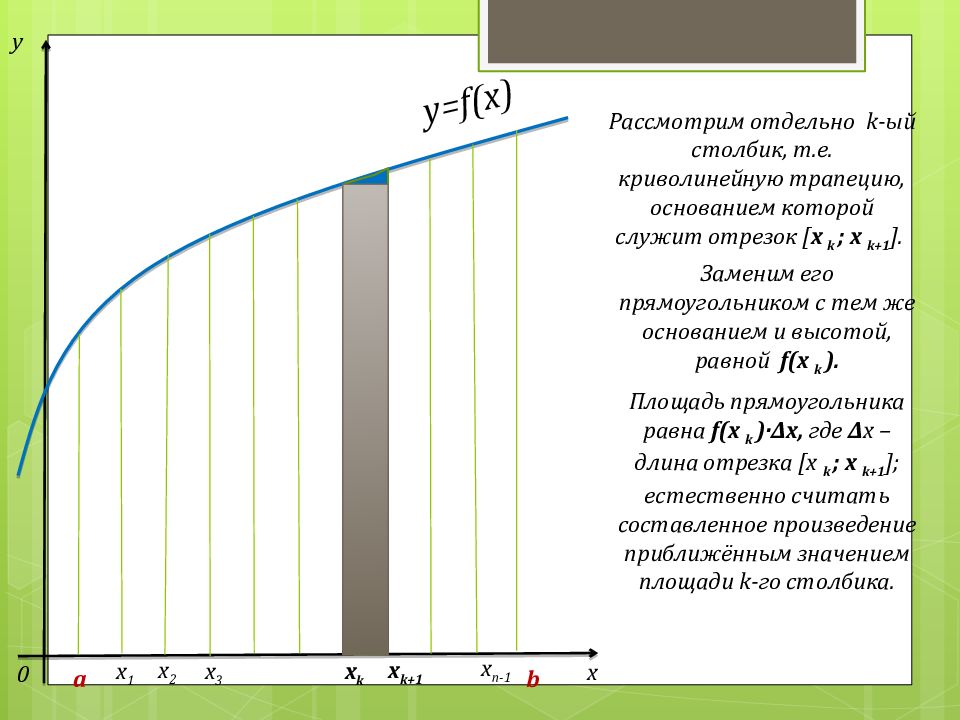
у х 0 y=f(x) x 1 x 2 x 3 x n -1 x k x k+1 a b Рассмотрим отдельно k -ый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок [ х k ; х k +1 ]. Площадь прямоугольника равна f (х k )· Δ х, где Δ х – длина отрезка [х k ; х k +1 ]; естественно считать составленное произведение приближённым значением площади k -го столбика. Заменим его прямоугольником с тем же основанием и высотой, равной f (х k ).
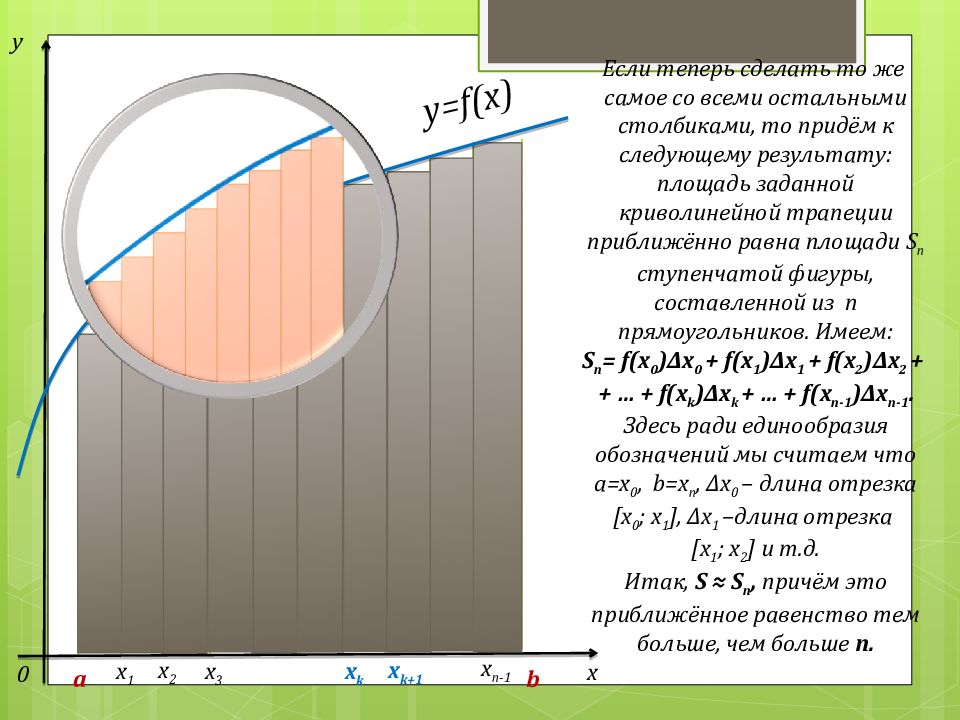
у х 0 y=f(x) x 1 x 2 x 3 x n -1 x k x k+1 a b Если теперь сделать то же самое со всеми остальными столбиками, то придём к следующему результату: площадь заданной криволинейной трапеции приближённо равна площади S n ступенчатой фигуры, составленной из n прямоугольников. Имеем: S n = f(x 0 ) Δ x 0 + f(x 1 ) Δ x 1 + f(x 2 ) Δ x 2 + + … + f(x k ) Δ x k + … + f(x n-1 ) Δ x n-1. Здесь ради единообразия обозначений мы считаем что а=х 0, b =х n, Δ x 0 – длина отрезка [ x 0 ; x 1 ], Δ x 1 – длина отрезка [ x 1 ; x 2 ] и т.д. Итак, S ≈ S n, причём это приближённое равенство тем больше, чем больше n.
Принято считать, что искомая площадь есть предел последовательности ( S n )
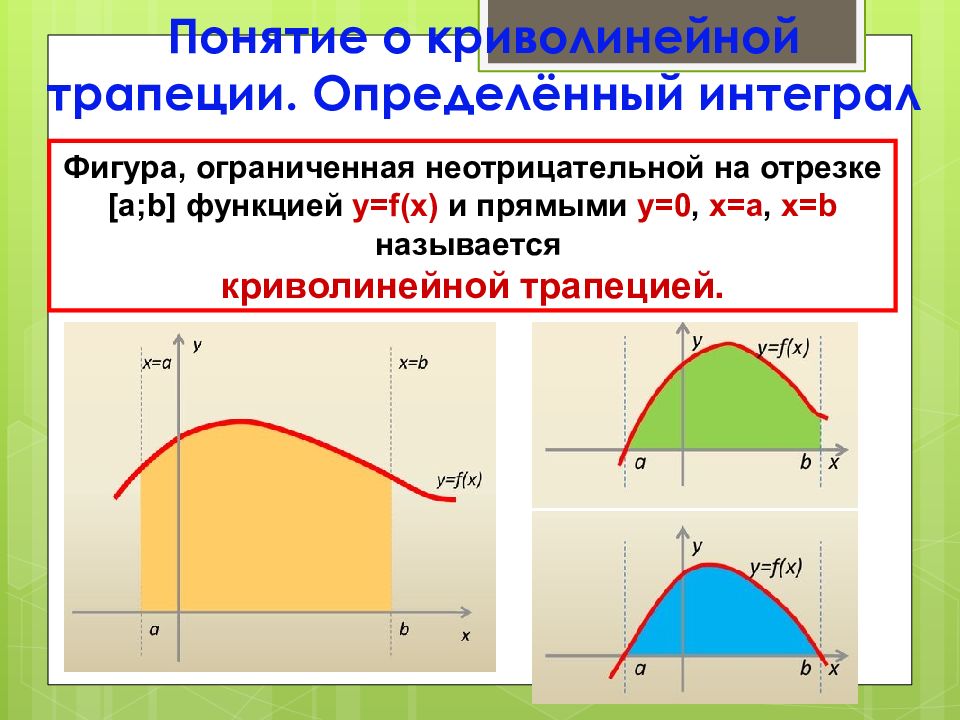
Понятие о криволинейной трапеции. Определённый интеграл Фигура, ограниченная неотрицательной на отрезке [a;b] функцией y=f(x) и прямыми у=0, x=a, x=b называется криволинейной трапецией.
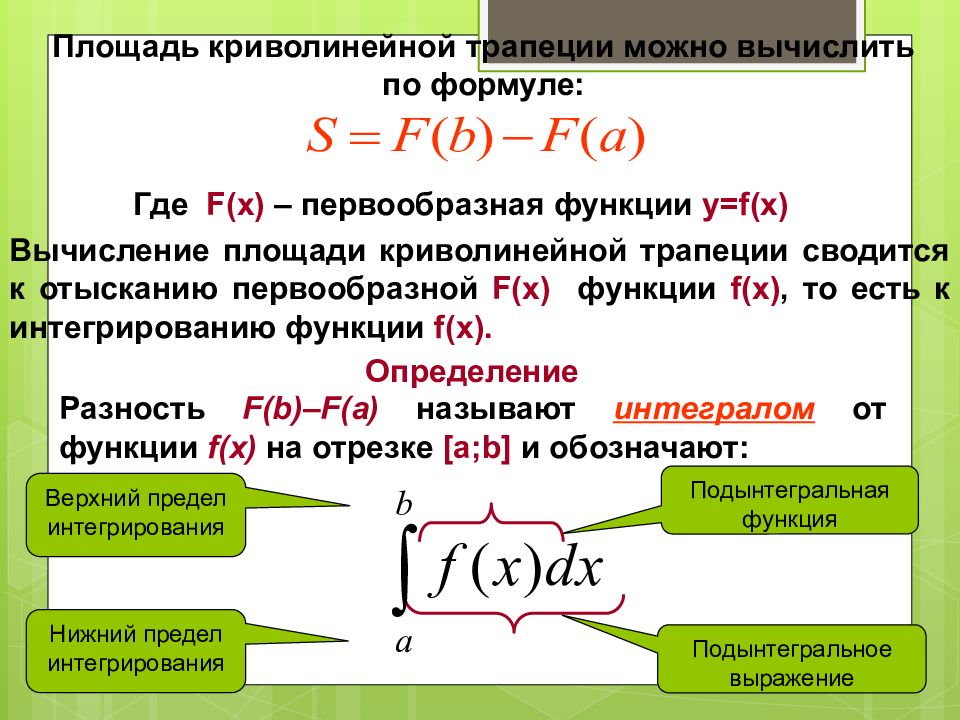
Площадь криволинейной трапеции можно вычислить по формуле: Где F(x) – первообразная функции y=f(x) Вычисление площади криволинейной трапеции сводится к отысканию первообразной F(x) функции f(x), то есть к интегрированию функции f(x). Определение Разность F(b)–F(a) называют интегралом от функции f(x) на отрезке [a;b] и обозначают: Подынтегральная функция Подынтегральное выражение Верхний предел интегрирования Нижний предел интегрирования
Формула Ньютона - Лейбница Исаак Ньютон 1642-1727 Готфрид Лейбниц 1646-1716 гг. Таким образом:
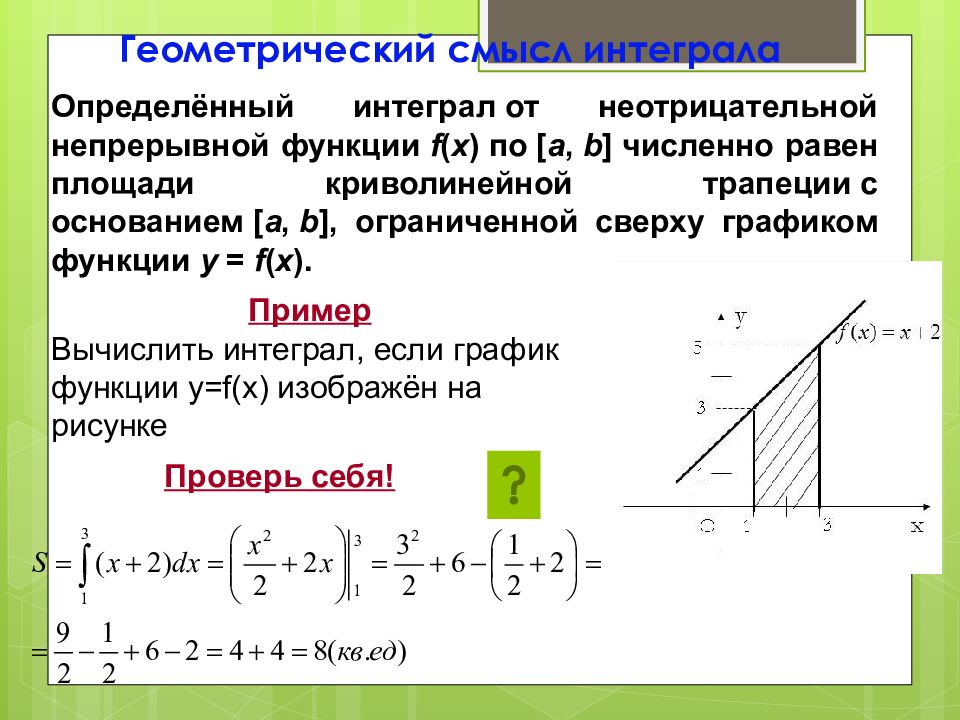
Геометрический смысл интеграла Определённый интеграл от неотрицательной непрерывной функции f ( x ) по [ a, b ] численно равен площади криволинейной трапеции с основанием [ a, b ], ограниченной сверху графиком функции y = f ( x ). Пример Вычислить интеграл, если график функции y=f(x) изображён на рисунке Проверь себя!
Физический смысл интеграла Материальная точка движется по прямой со скоростью, определяемой формулой v=3t 2 -4t+1, (время измеряется в секундах, скорость – в см/с). Какой путь пройдёт точка за 3 секунды, считая от начала движения ( t=0 )? При прямолинейном движении перемещение S численно равно определённому интегралу зависимости скорости V от времени t Пример
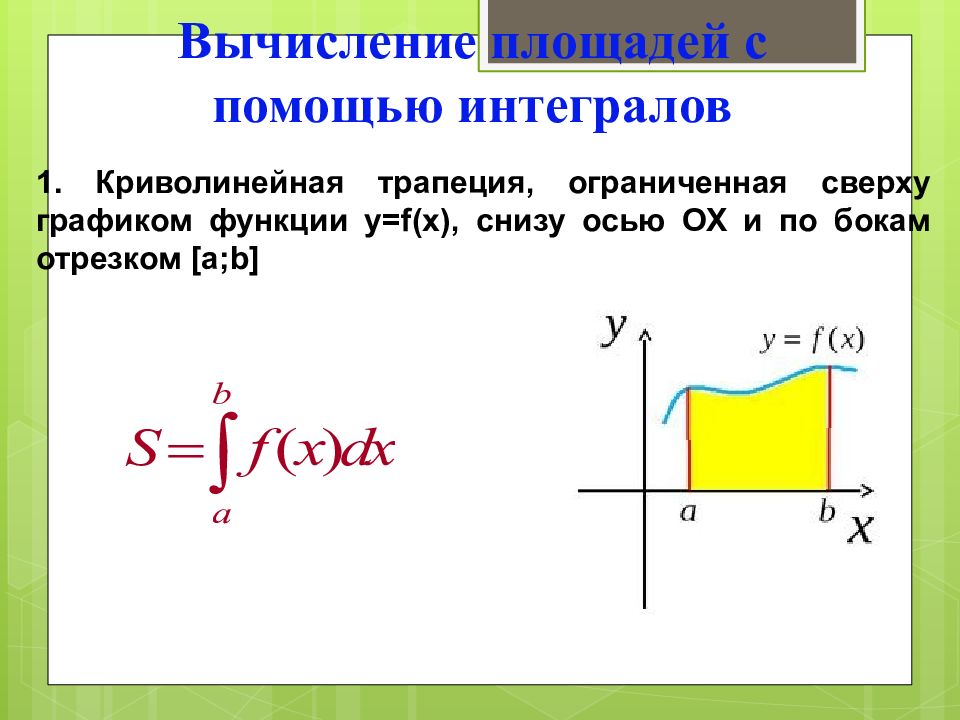
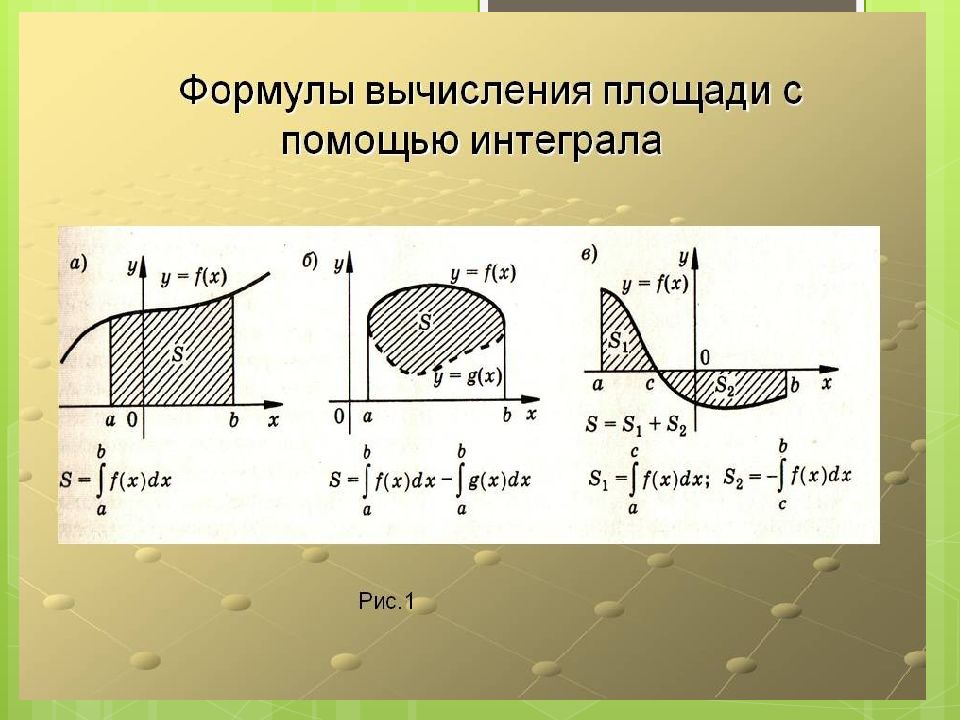
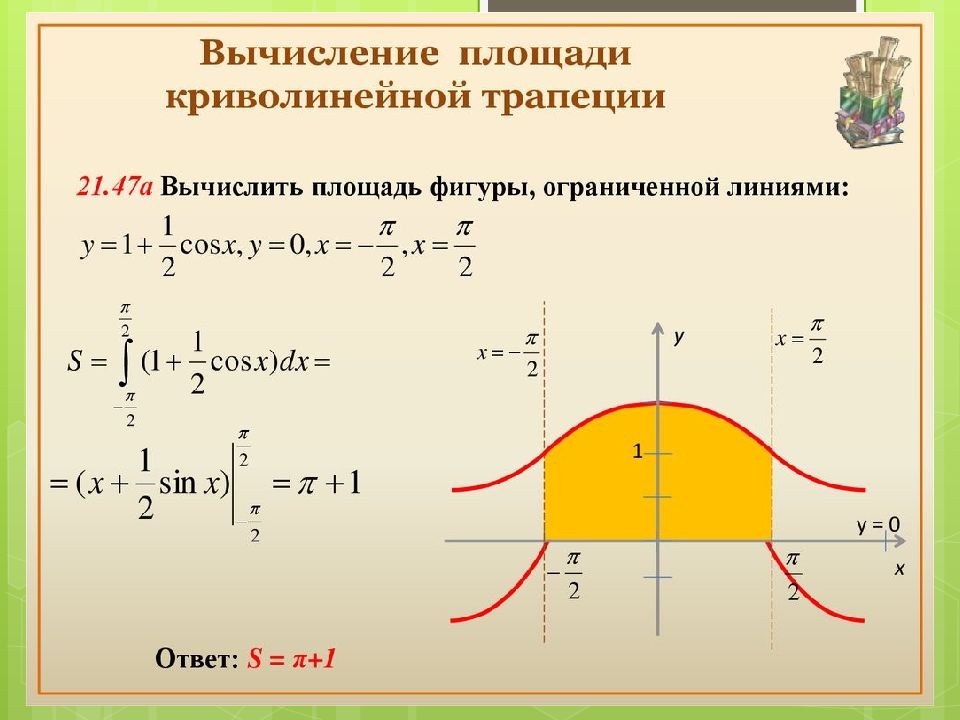
Вычисление площадей с помощью интегралов 1. Криволинейная трапеция, ограниченная сверху графиком функции y=f(x), снизу осью ОХ и по бокам отрезком [a;b]
2. Фигура, ограниченная сверху только графиком функции y=f(x) и снизу осью ОХ Точки а и b находим из уравнения f(x) =0 3. Криволинейная трапеция, ограниченная сверху осью ОХ, снизу графиком функции y=f(x) и по бокам отрезком [a;b]
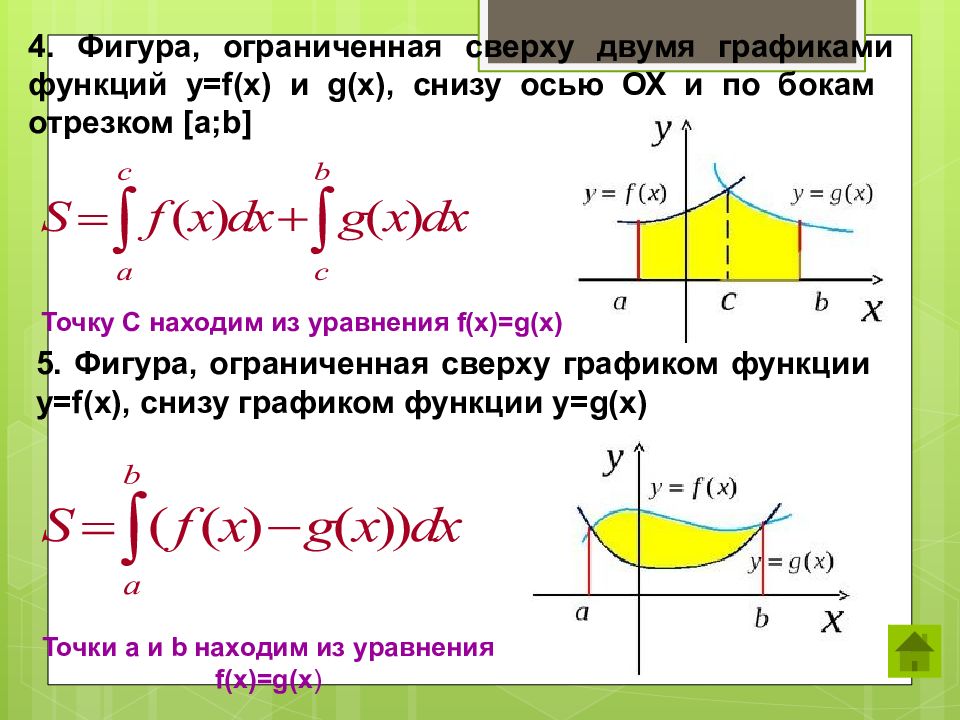
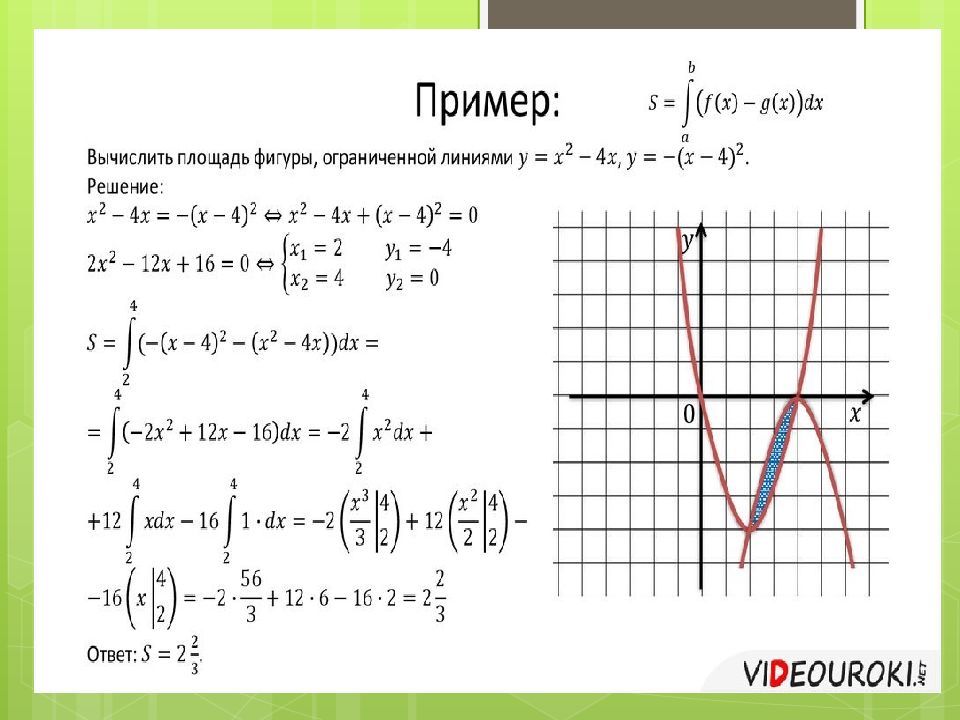
4. Фигура, ограниченная сверху двумя графиками функций y=f(x) и g(x), снизу осью ОХ и по бокам отрезком [a;b] Точку С находим из уравнения f(x)=g(x) 5. Фигура, ограниченная сверху графиком функции y=f(x), снизу графиком функции y=g(x) Точки a и b находим из уравнения f(x)=g(x )
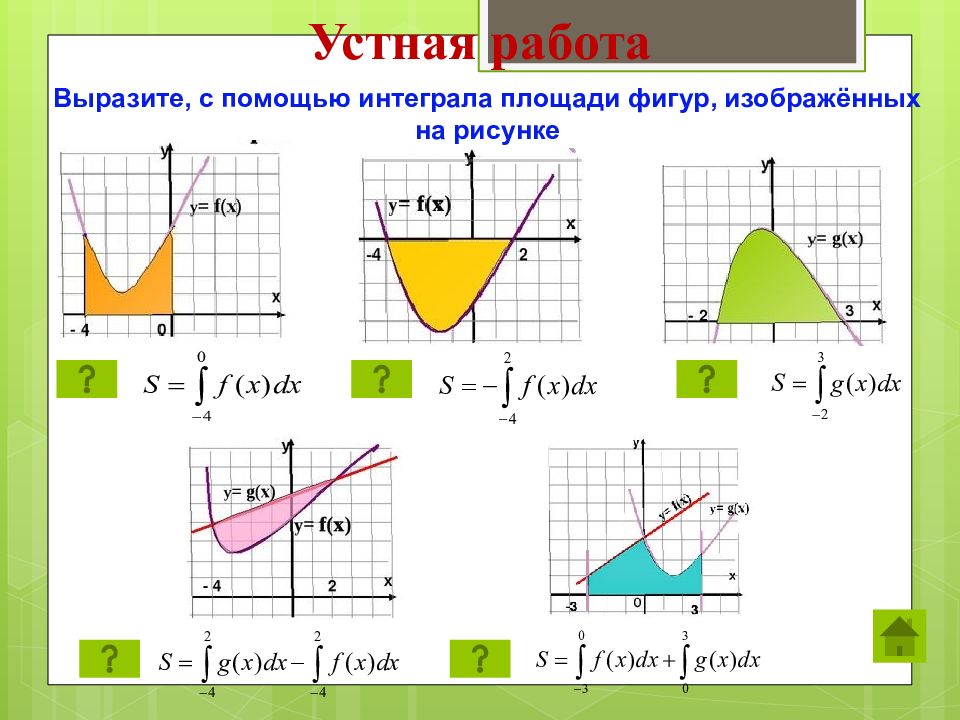
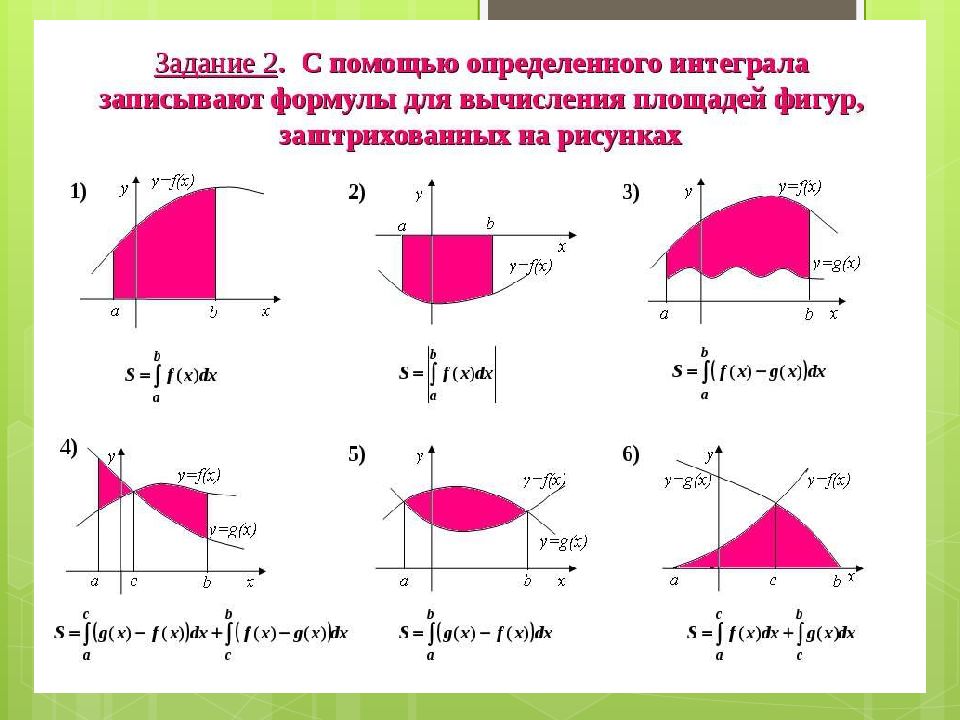
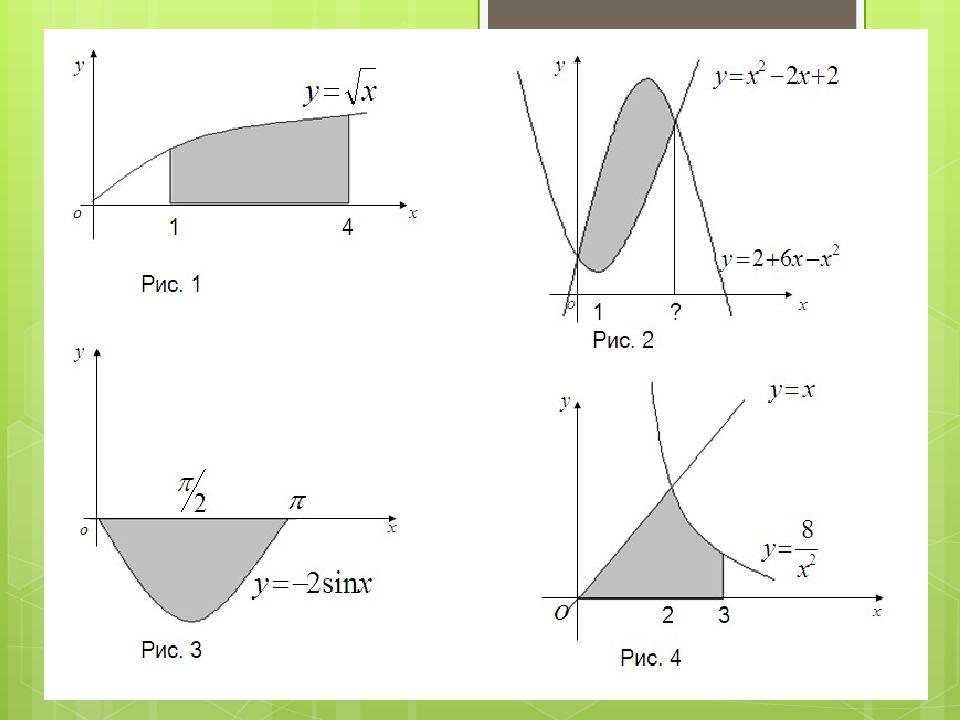
Устная работа Выразите, с помощью интеграла площади фигур, изображённых на рисунке
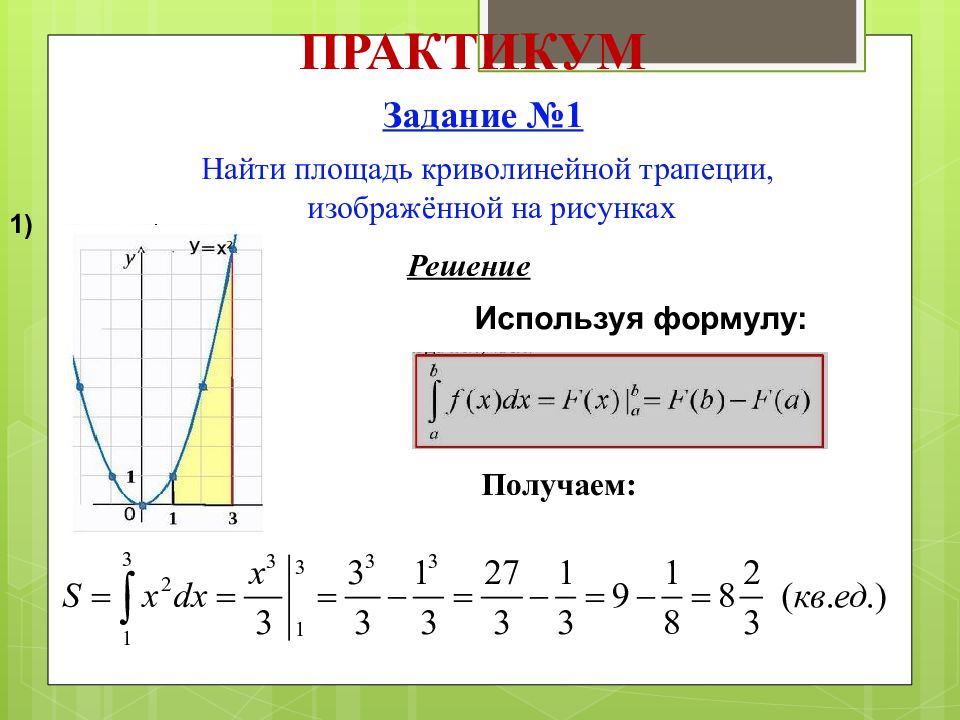
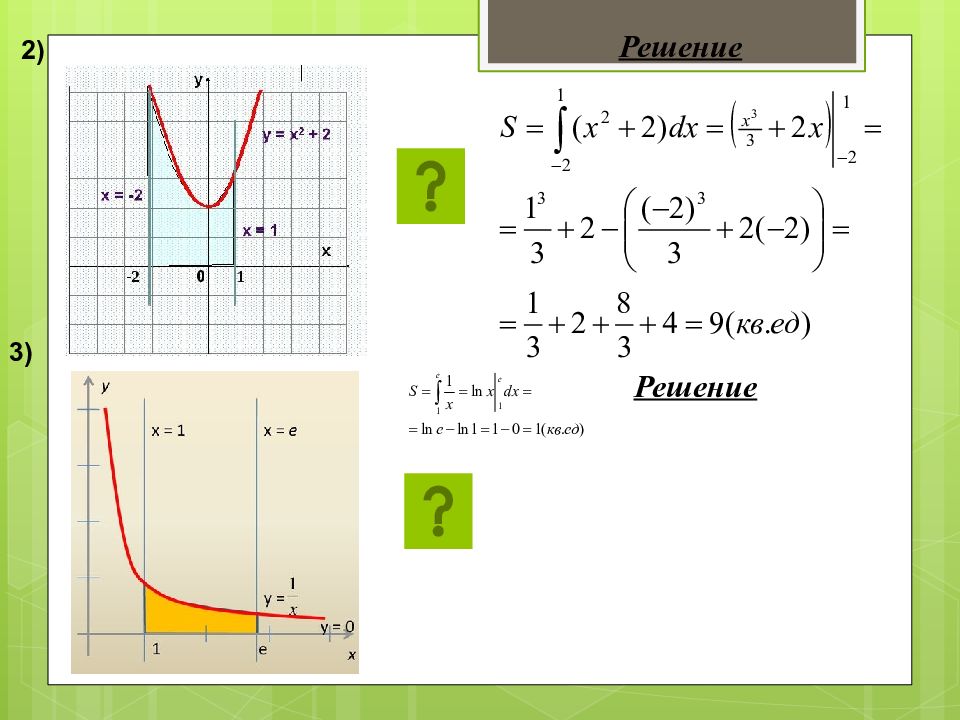
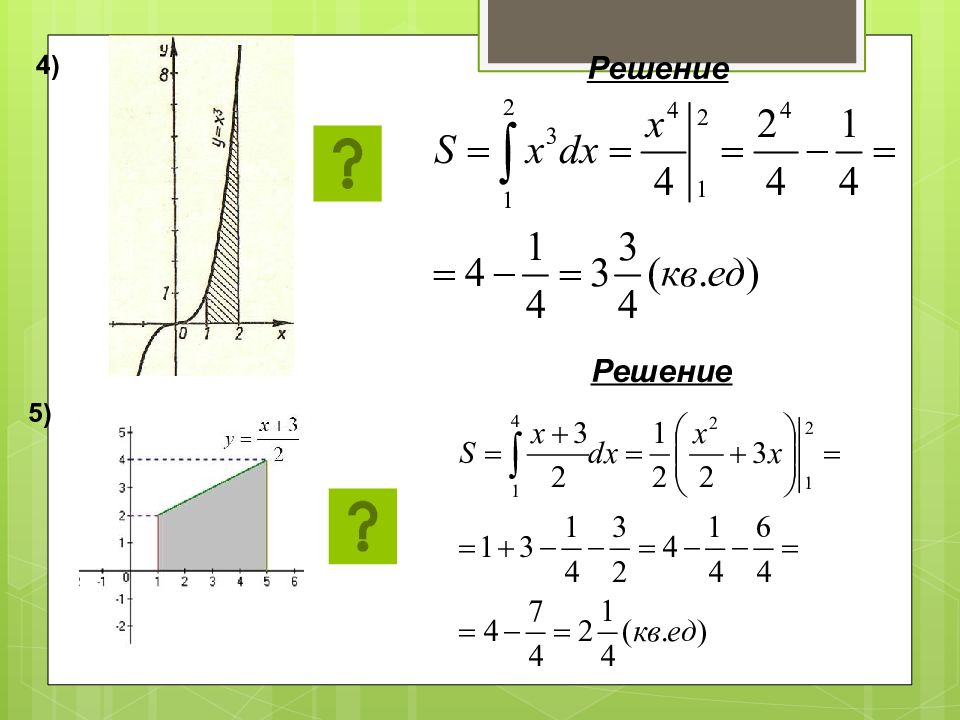
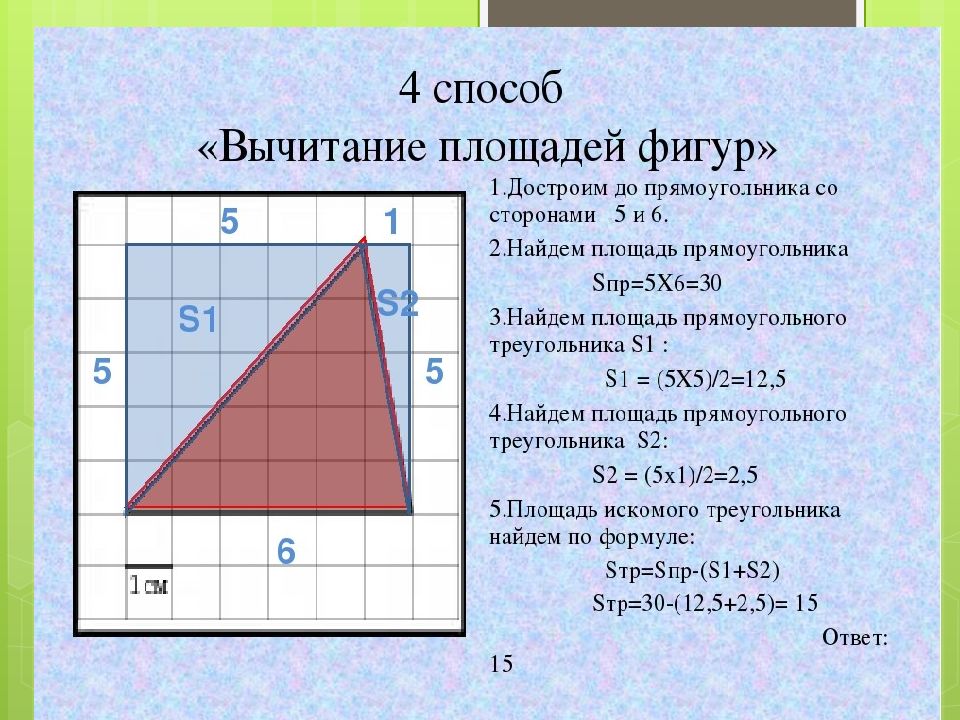
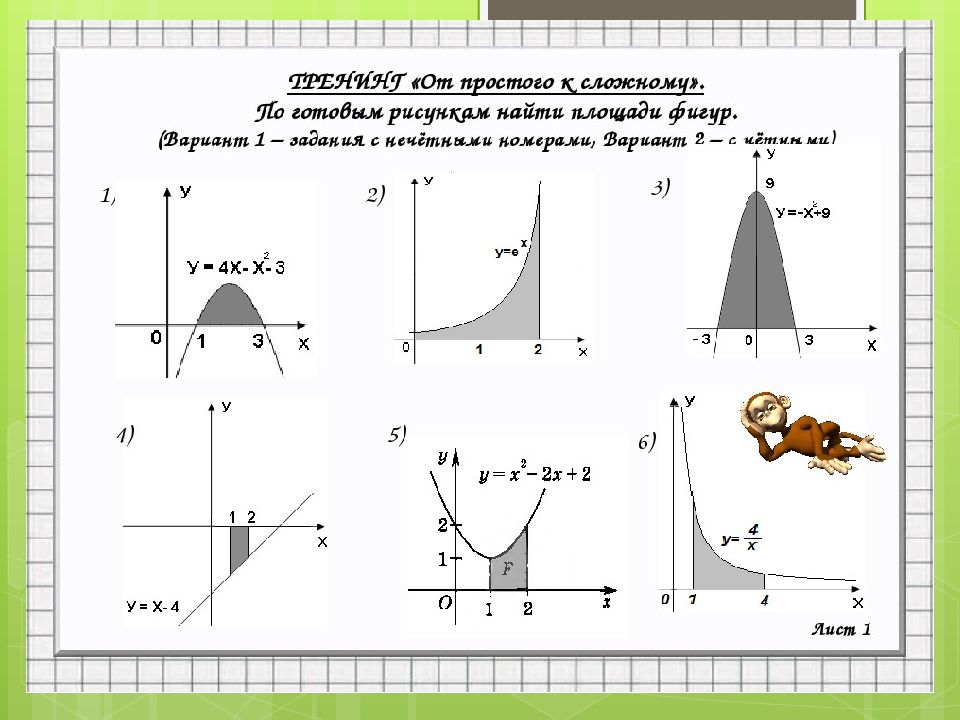
ПРАКТИКУМ Задание №1 Найти площадь криволинейной трапеции, изображённой на рисунках Используя формулу: Решение Получаем: 1)
2) Решение 3) Решение
4) Решение 5) Решение
6) находится в I четверти Решение 7) Решение
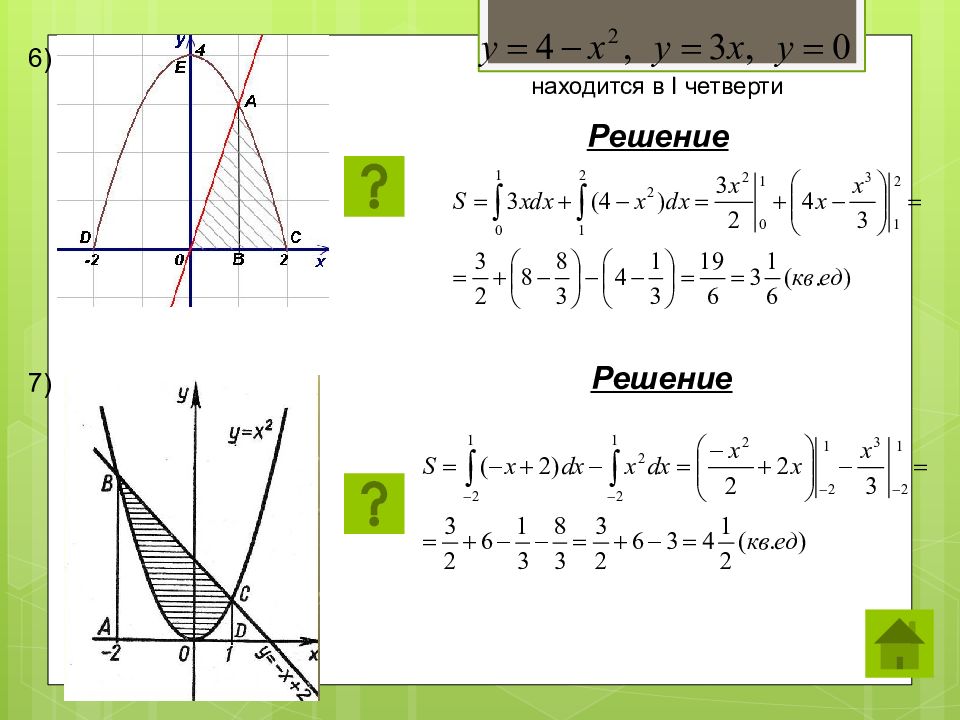
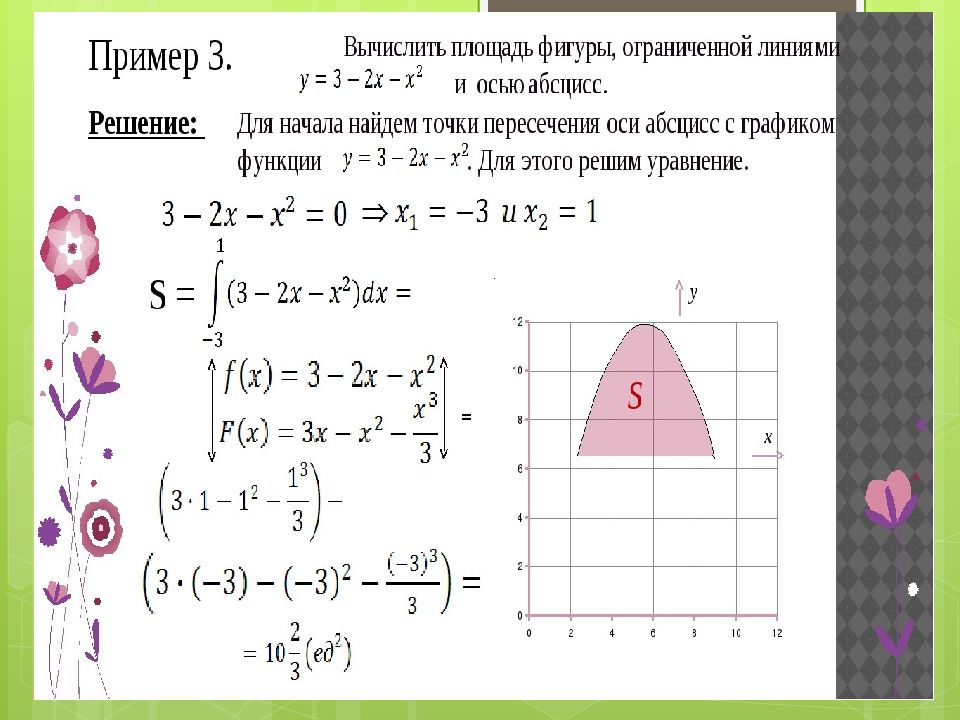
Вычислите площадь фигуры, ограниченной линиями (схематично изобразив графики функций). Ответ: 1) 4,5 2) 9/8 3) 4,5 4)1/3 ЗАДАНИЕ №2 Вычислить площадь фигуры, ограниченной линиями и осью ОХ, если ЗАДАНИЕ № 3
