29.09.20 г. ? прямые
а II b Взаимное расположение двух прямых в пространстве М a b a b а b
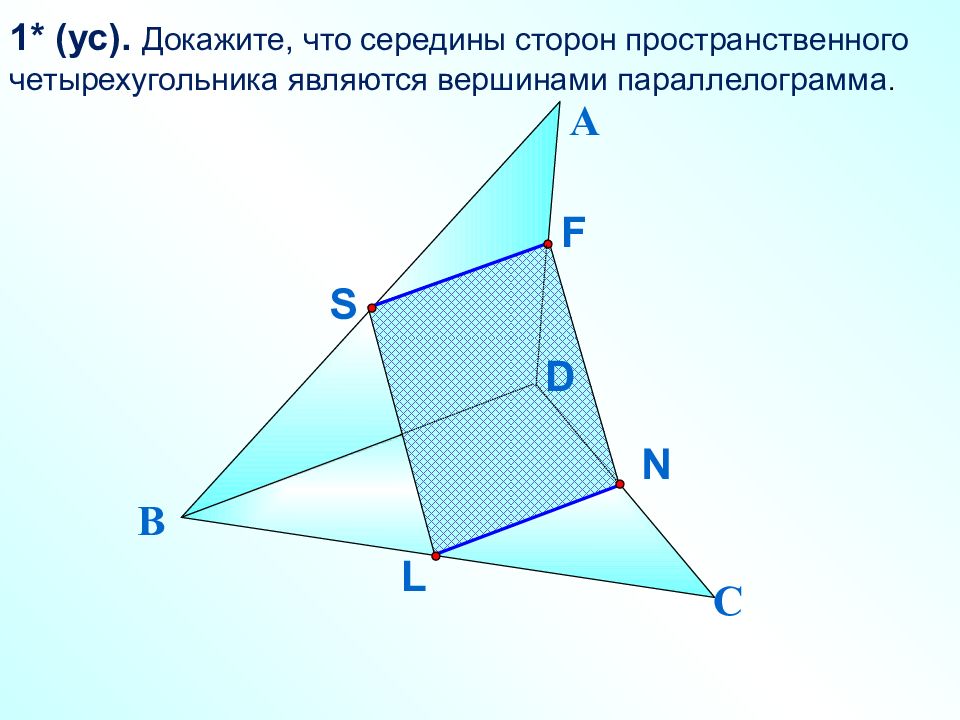
1* (ус). Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма. А В С F S L N D
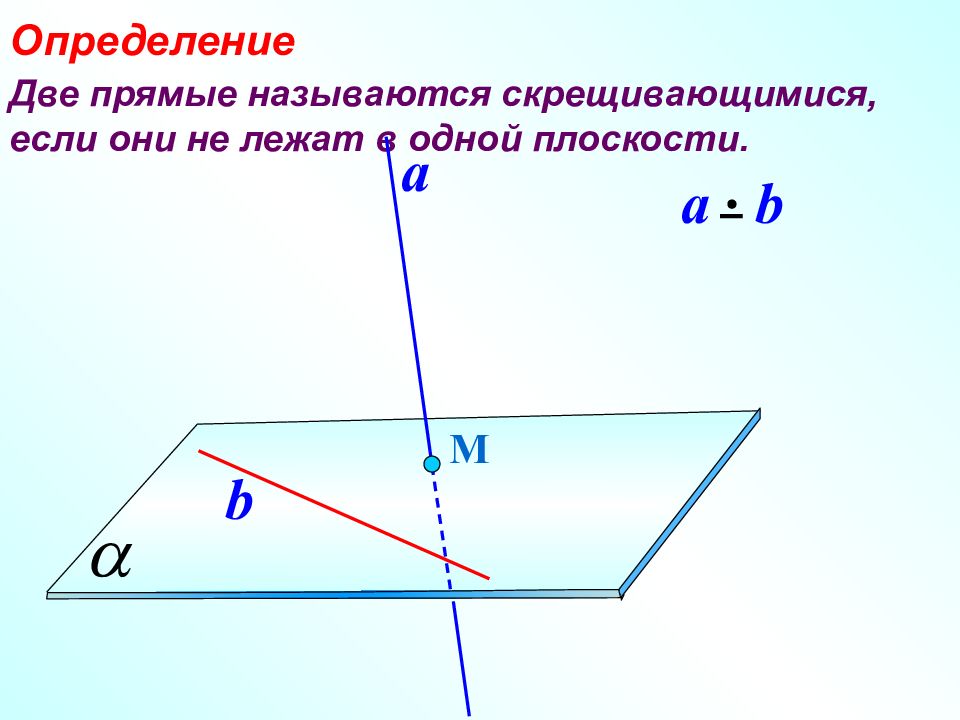
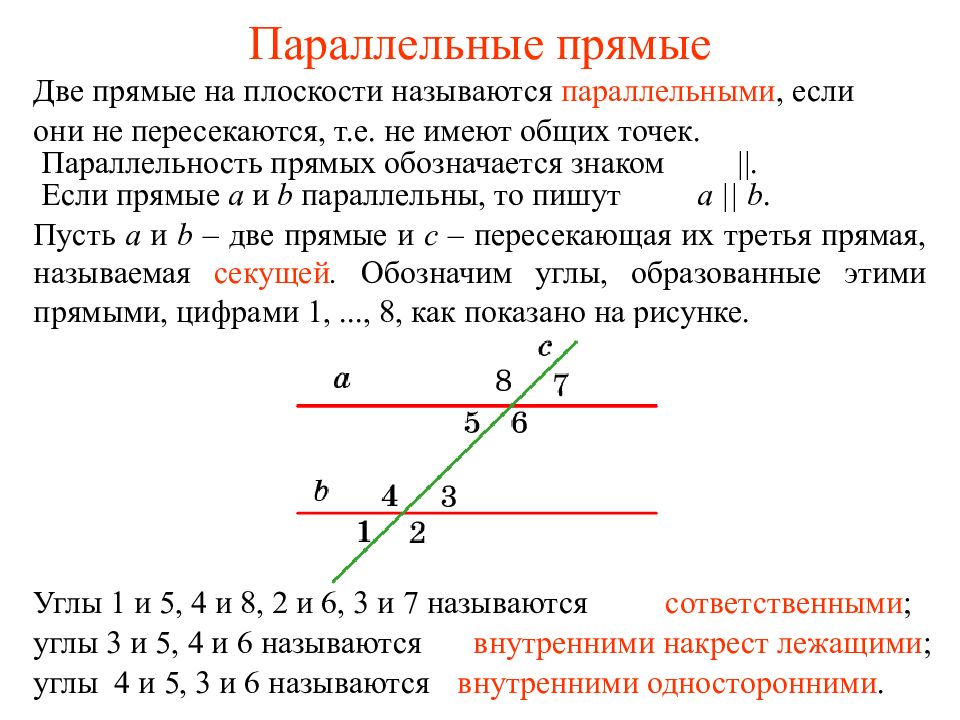
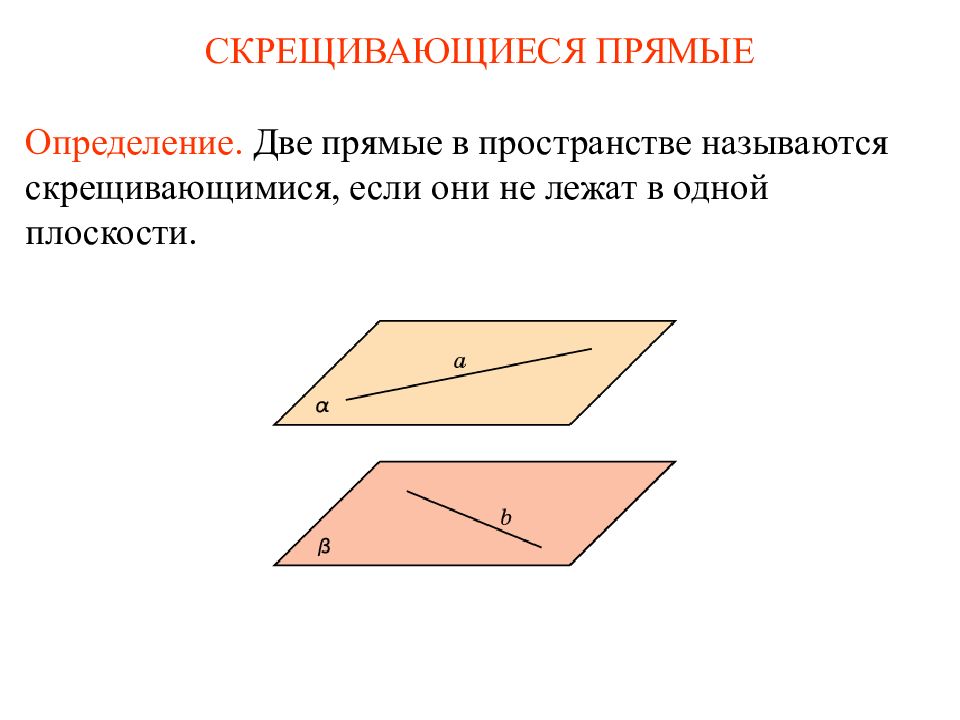
Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Определение М a b a b
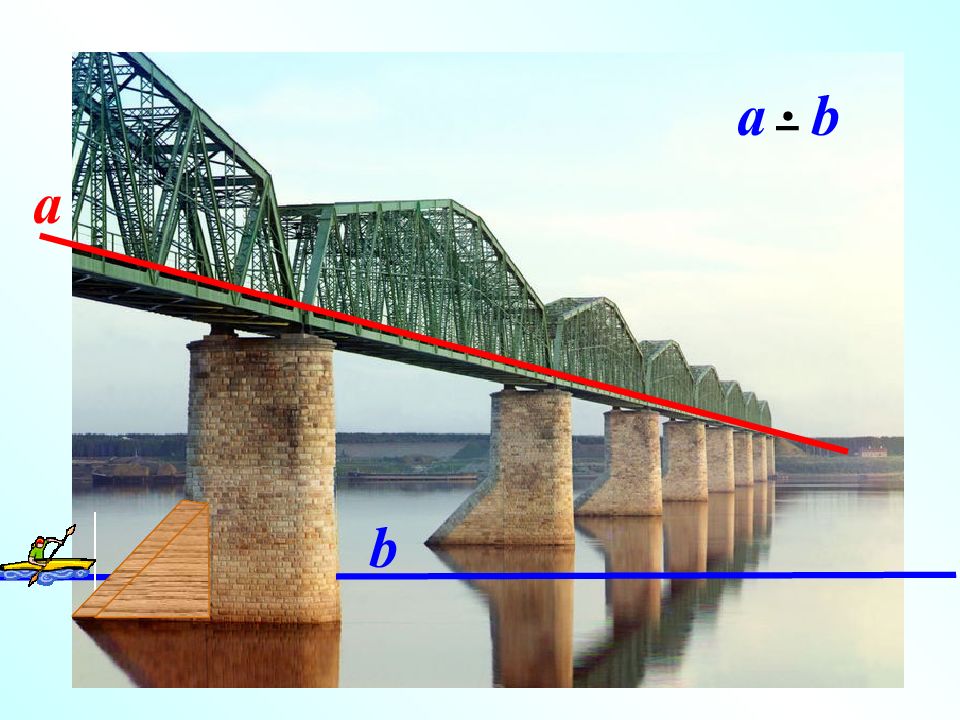
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой
a b a b
Найдите на рисунке параллельные прямые. Назовите параллельные прямые и плоскости. Найдите скрещивающиеся прямые
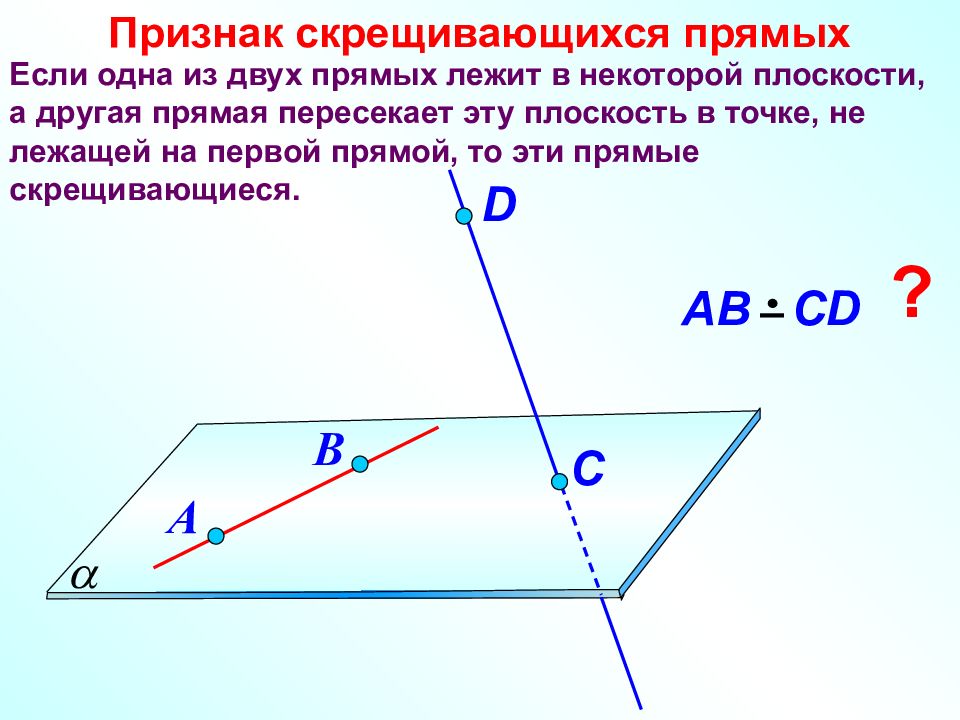
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся. Признак скрещивающихся прямых D В АВ С D А C ?
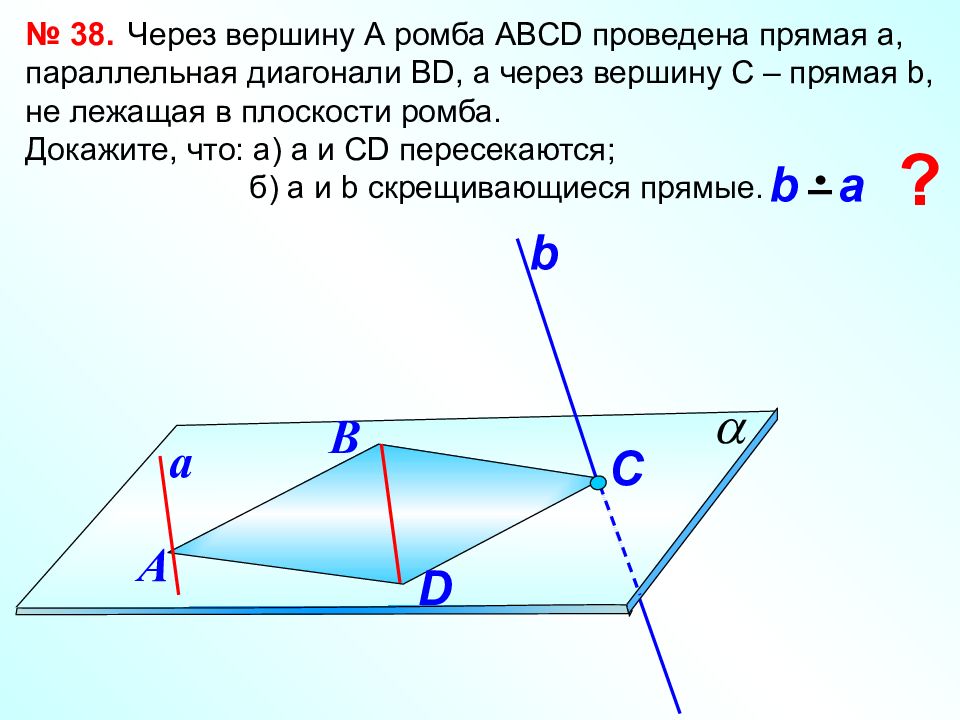
№ 38. Через вершину А ромба АВС D проведена прямая а, параллельная диагонали В D, а через вершину С – прямая b, не лежащая в плоскости ромба. Докажите, что: а) а и С D пересекаются; б) а и b скрещивающиеся прямые. В b a А C ? a b D
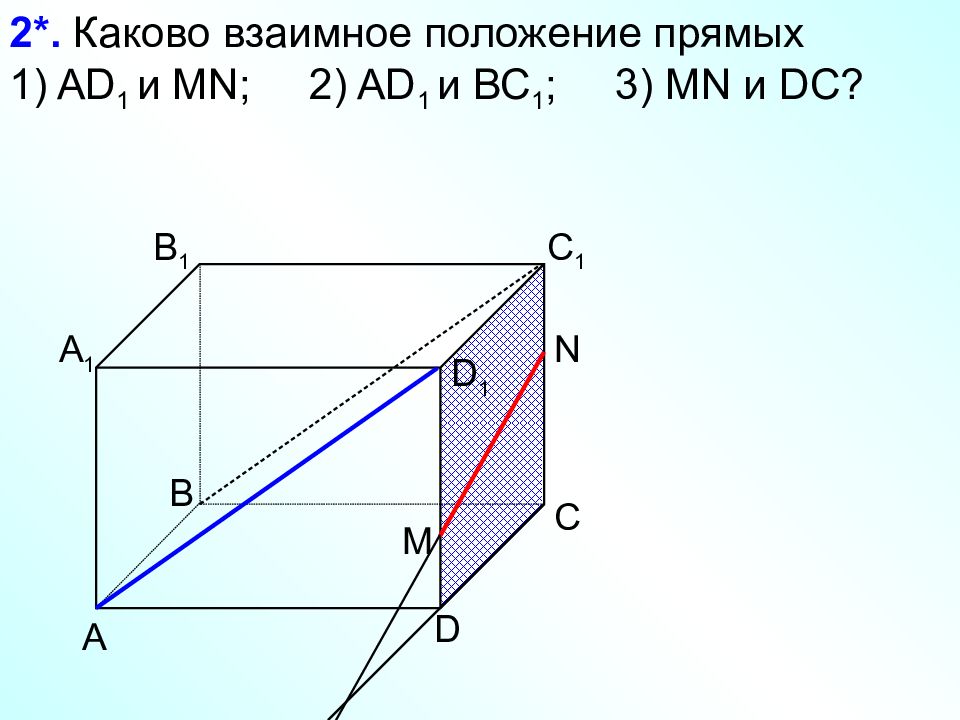
А D С В B 1 С 1 D 1 А 1 2*. Каково взаимное положение прямых 1) AD 1 и М N; 2) AD 1 и ВС 1 ; 3) М N и DC ? N M
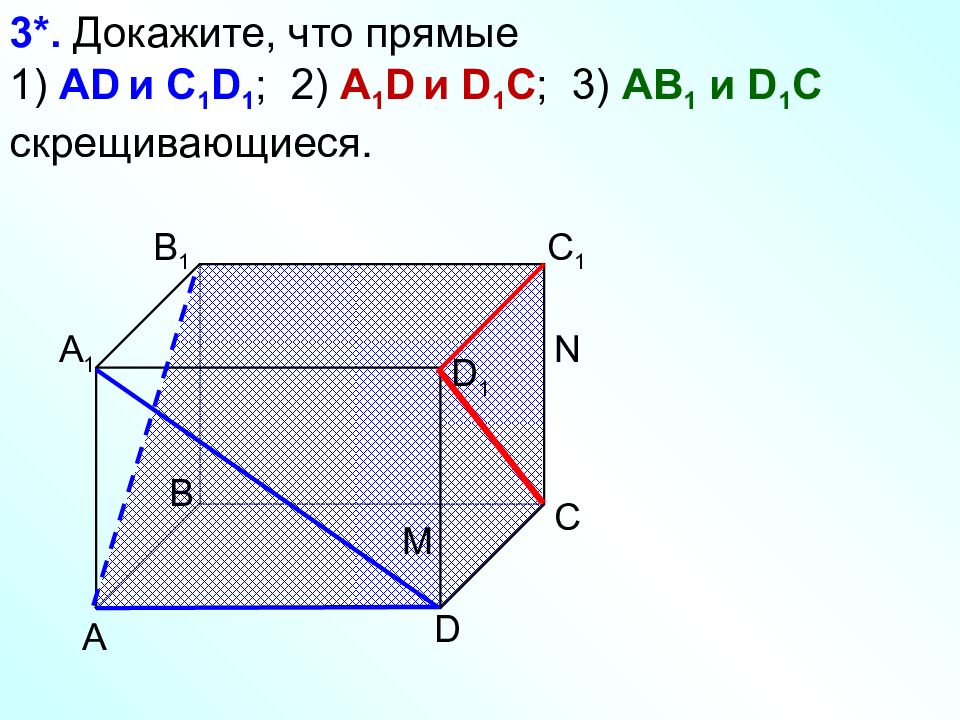
А D С В B 1 С 1 D 1 А 1 3*. Докажите, что прямые 1) AD и C 1 D 1 ; 2) A 1 D и D 1 C ; 3) AB 1 и D 1 C скрещивающиеся. N M
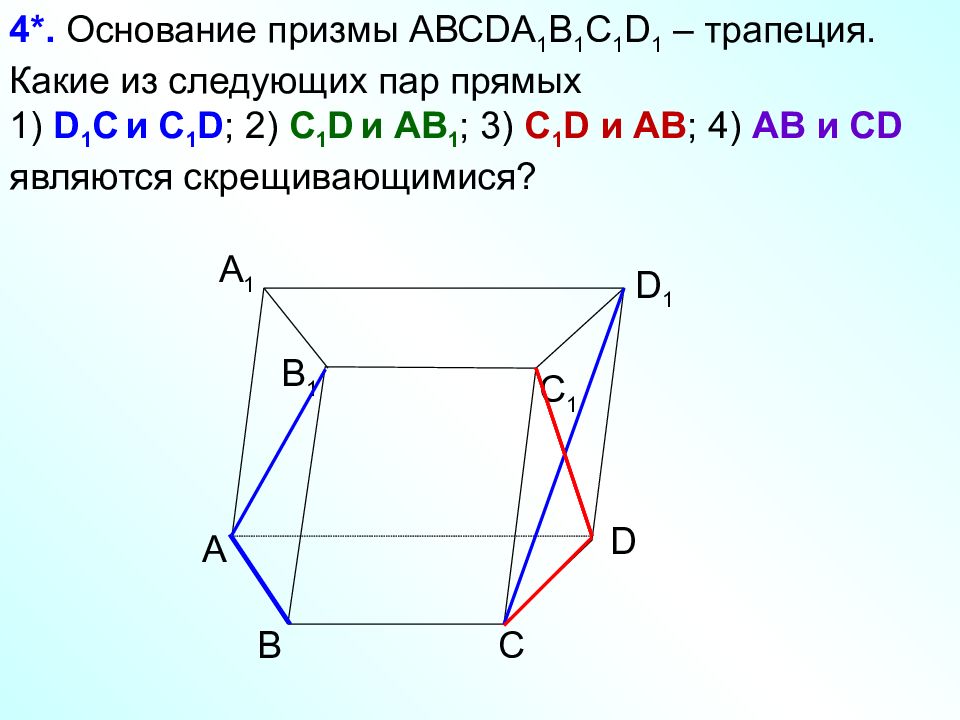
А D С В B 1 С 1 D 1 А 1 4*. Основание призмы АВС DA 1 B 1 C 1 D 1 – трапеция. Какие из следующих пар прямых 1) D 1 C и C 1 D ; 2) C 1 D и AB 1 ; 3) C 1 D и AB ; 4) AB и CD являются скрещивающимися?
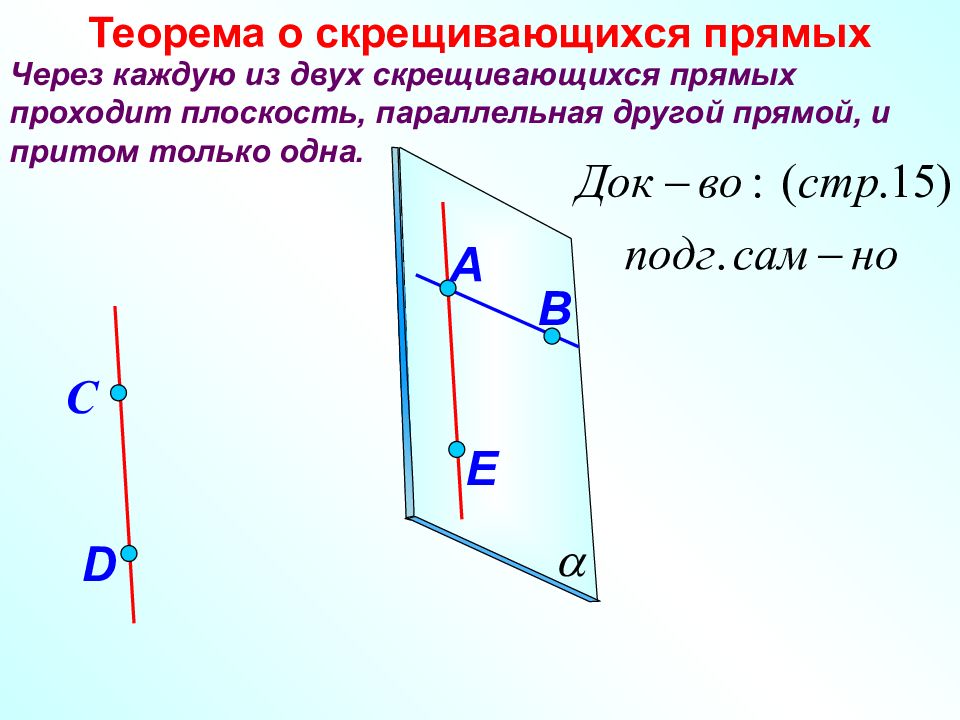
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теорема о скрещивающихся прямых D С B E A
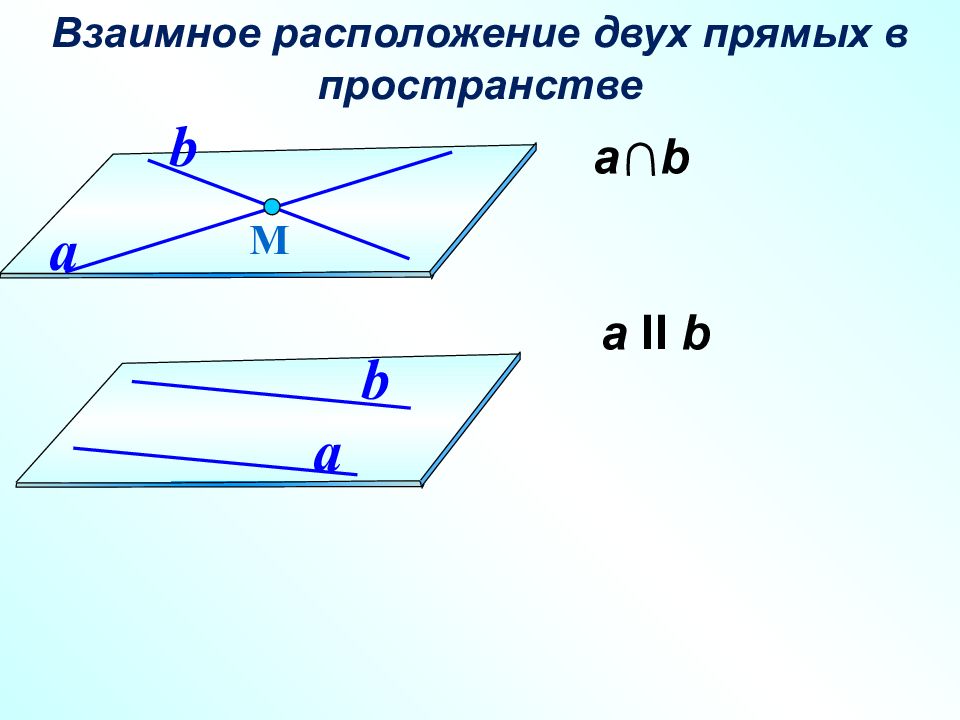
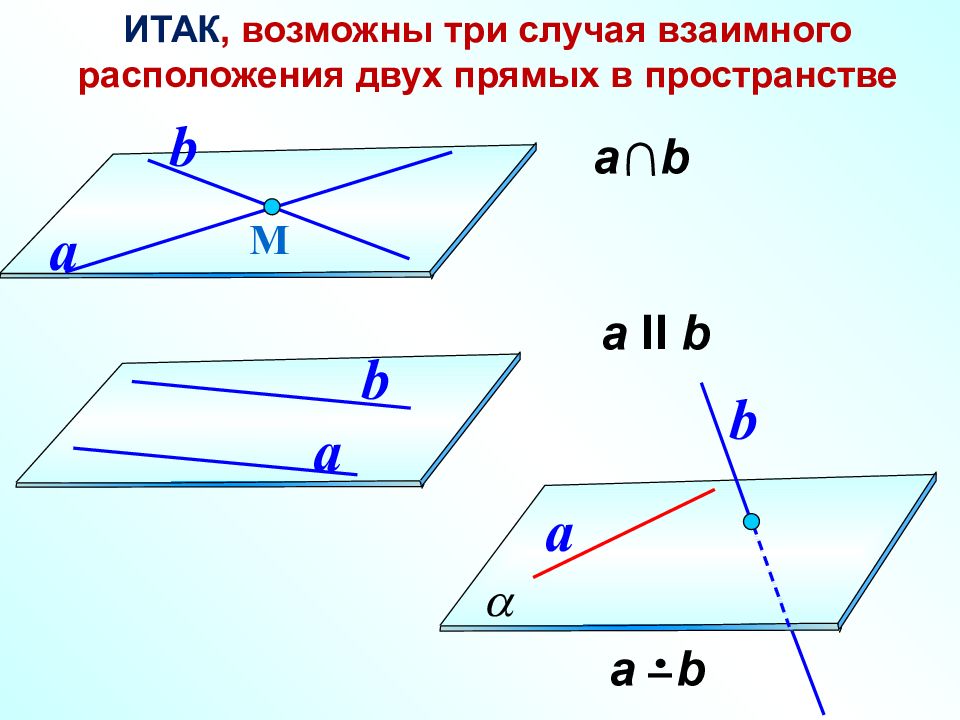
а II b ИТАК, возможны три случая взаимного расположения двух прямых в пространстве а b М a b a b a b а b
На уроке: 1) Новая тема: №1*, 38, 2* - 4* 2) №34, 39 Дома: п. 7, наиз. определения и теорему, ?1 – 12 (с.31) №35, 36, 37
