Первый слайд презентации: Содержание
Аксиомы стереометрии (введение) Параллельность прямых, прямой и плоскости (гл.1 §1) Взаимное расположение прямых в пространстве (гл.1 §2) Скрещивающиеся прямые (п. 7) Угол между прямыми (п. 9) Параллельность плоскостей
Слайд 2: Аксиомы стереометрии
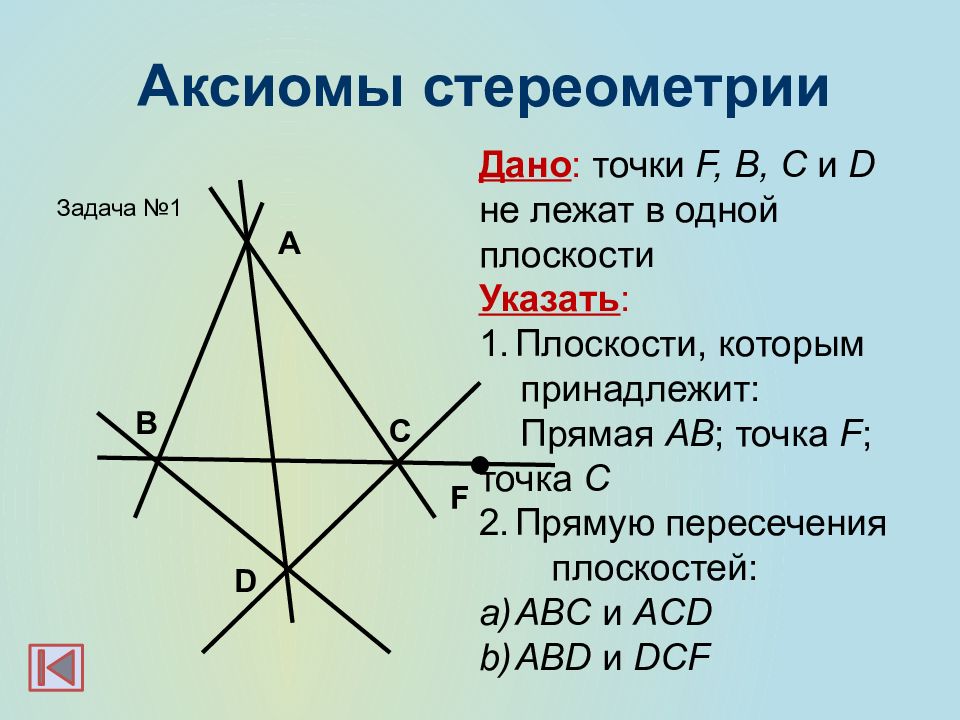
C D B F A Дано : точки F, B, C и D не лежат в одной плоскости Указать : Плоскости, которым принадлежит: Прямая AB ; точка F ; точка С Прямую пересечения плоскостей: ABC и ACD ABD и DCF Задача №1
Слайд 3: Аксиомы стереометрии
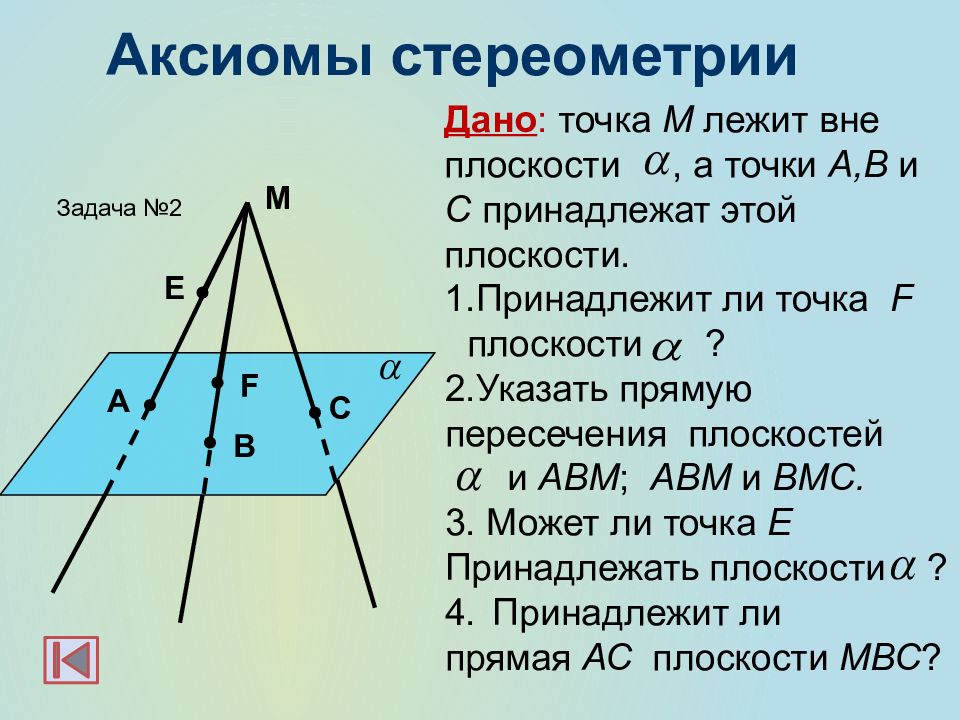
M E F C A B Дано : точка M лежит вне плоскости, а точки A,B и C принадлежат этой плоскости. Принадлежит ли точка F плоскости ? 2.Указать прямую пересечения плоскостей и ABM ; ABM и ВМС. 3. Может ли точка E Принадлежать плоскости ? Принадлежит ли прямая АС плоскости МВС ? Задача №2 Аксиомы стереометрии
Слайд 4: Аксиомы стереометрии
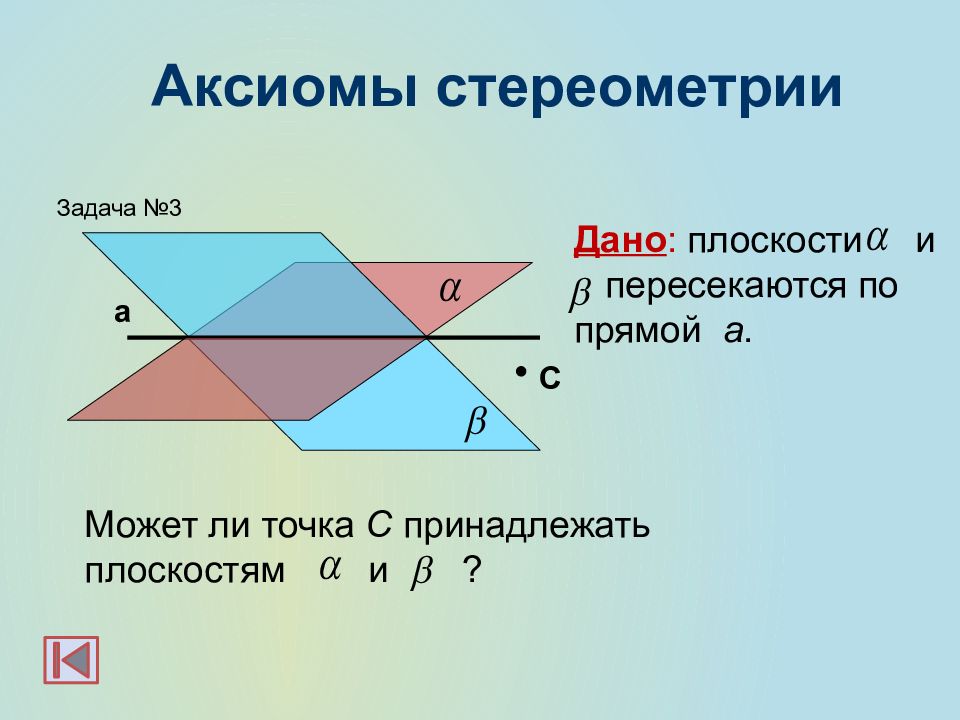
C Дано : плоскости и пересекаются по прямой а. Может ли точка С принадлежать плоскостям и ? Задача №3 а
Слайд 5: Аксиомы стереометрии
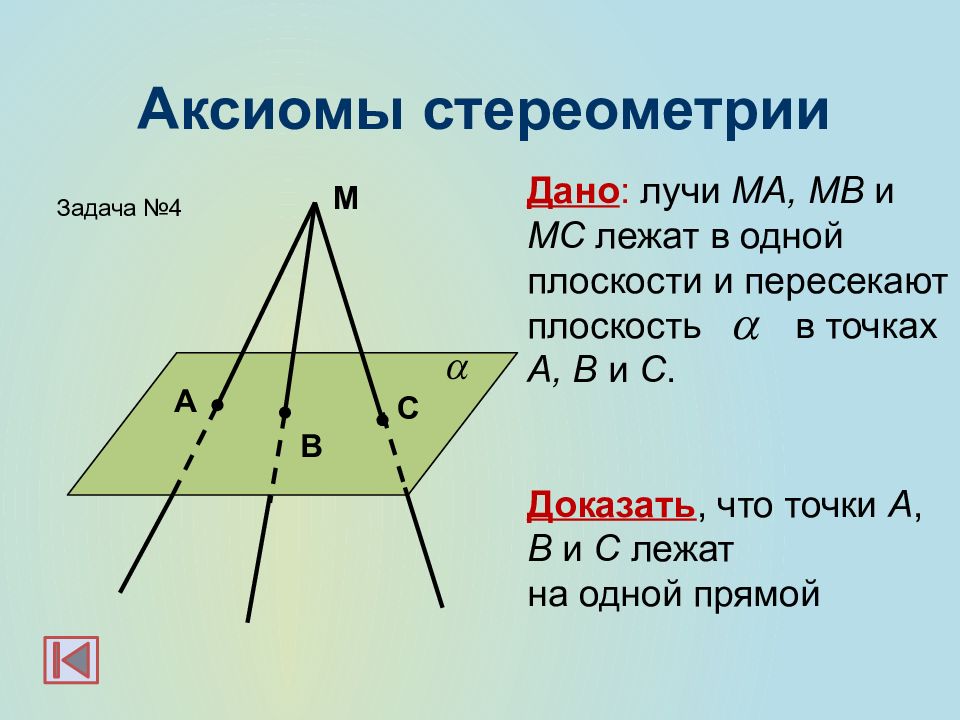
M C A B Дано : лучи MA, MB и MC лежат в одной плоскости и пересекают плоскость в точках A, B и C. Доказать, что точки A, B и C лежат на одной прямой Задача №4 Аксиомы стереометрии
Слайд 6: Аксиомы стереометрии
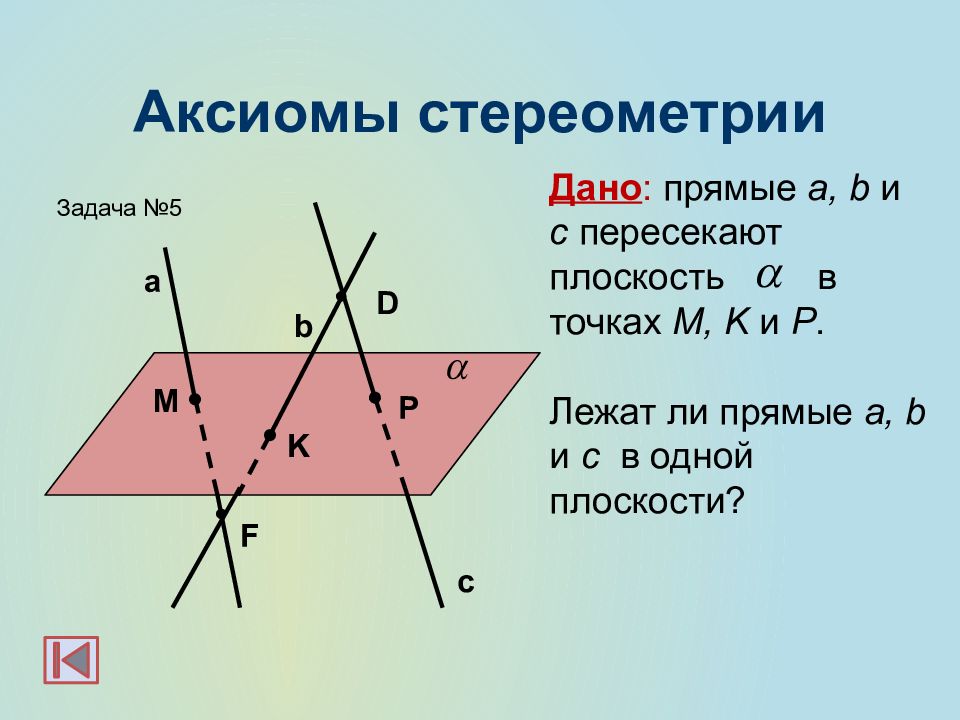
M P K F Дано : прямые a, b и с пересекают плоскость в точках M, K и P. Лежат ли прямые a, b и с в одной плоскости? Задача №5 D c a b
Слайд 7: Аксиомы стереометрии
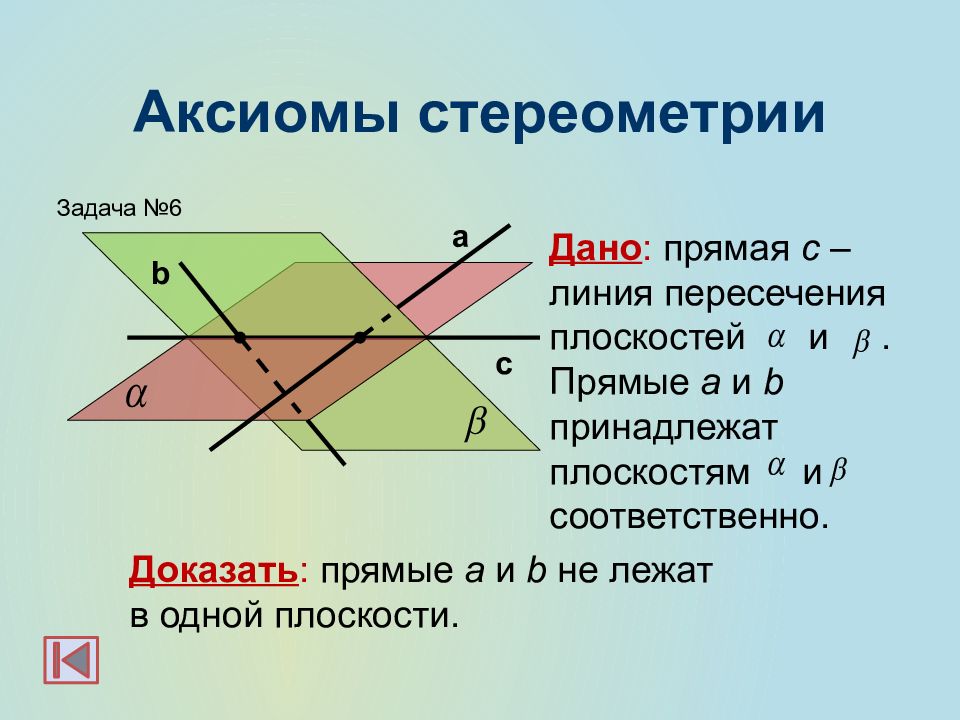
с Дано : прямая с – линия пересечения плоскостей и. Прямые a и b принадлежат плоскостям и соответственно. Доказать : прямые a и b не лежат в одной плоскости. Задача №6 b а
Слайд 8: Параллельность прямых
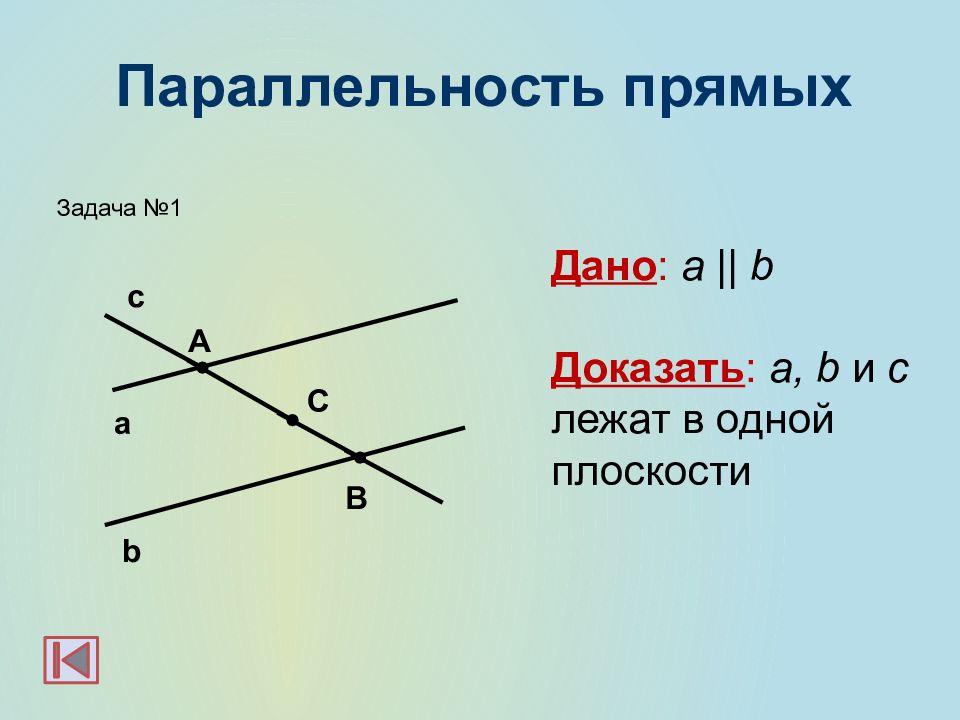
b а с А С В Дано : a || b Доказать : a, b и c лежат в одной плоскости Задача №1
Слайд 9: Параллельность прямых
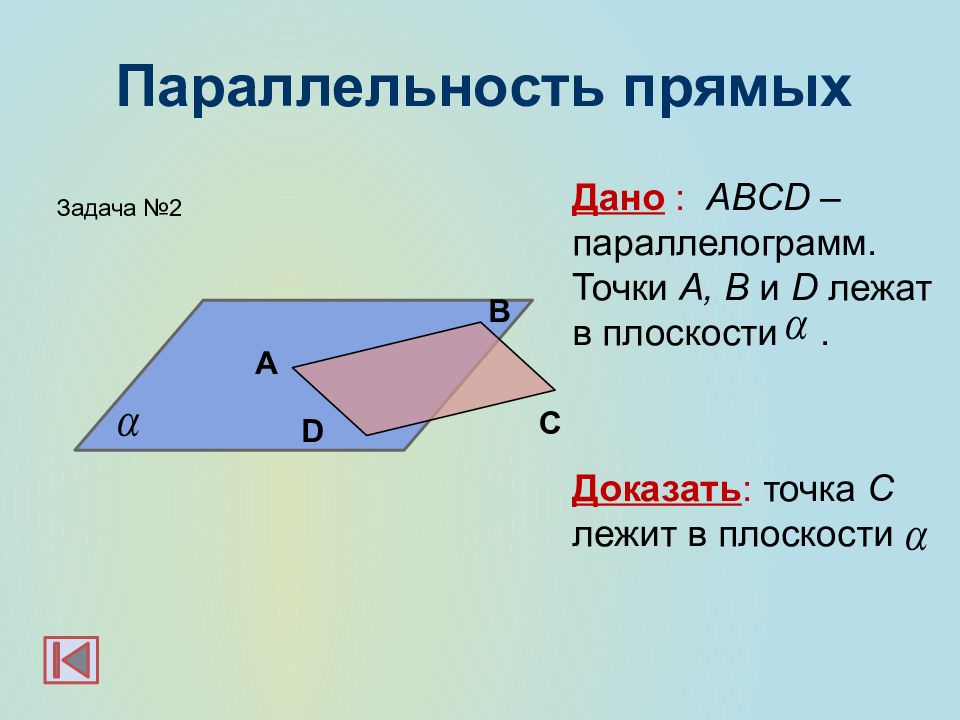
Дано : ABCD –параллелограмм. Точки A, B и D лежат в плоскости. Доказать : точка С лежит в плоскости А В С D Задача №2
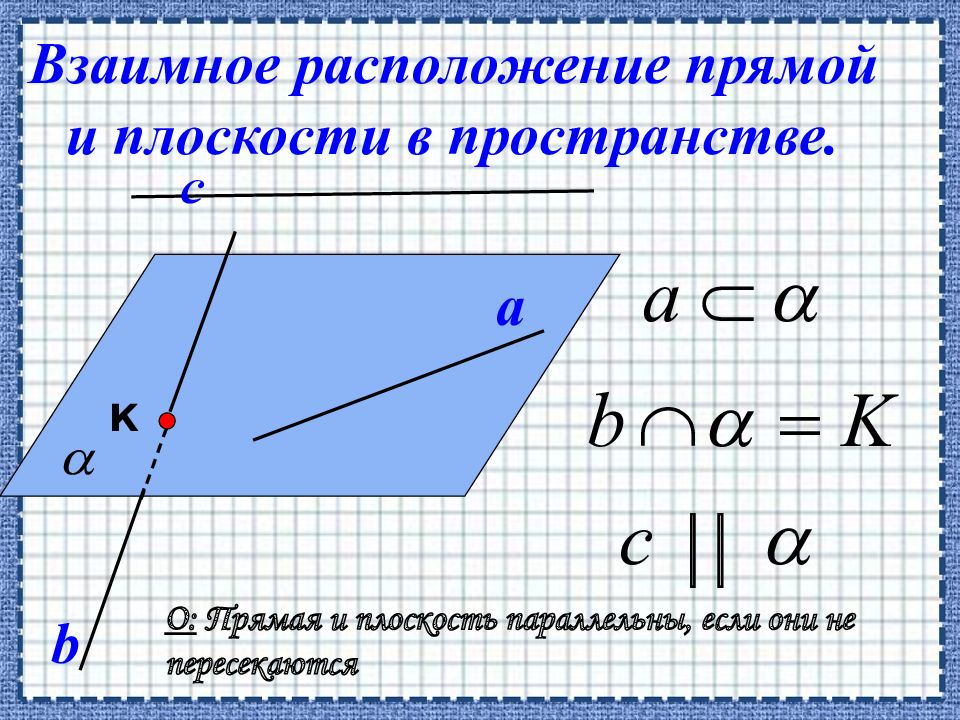
Слайд 10: Параллельность прямой и плоскости
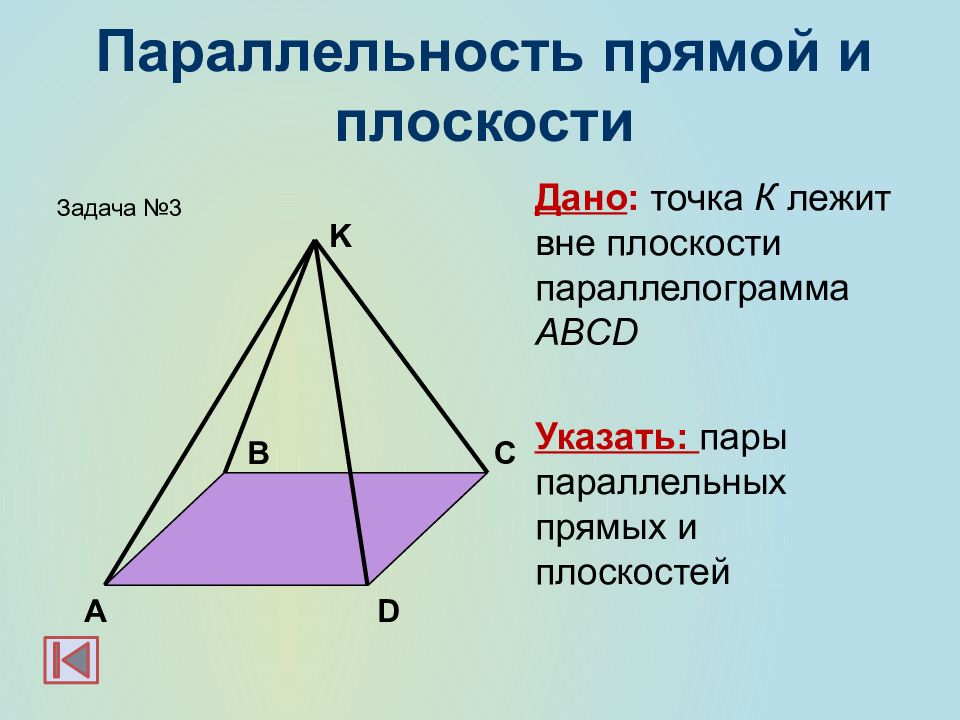
Дано : точка К лежит вне плоскости параллелограмма ABCD Указать: пары параллельных прямых и плоскостей А В С D K Задача №3
Слайд 11: Параллельность прямой и плоскости
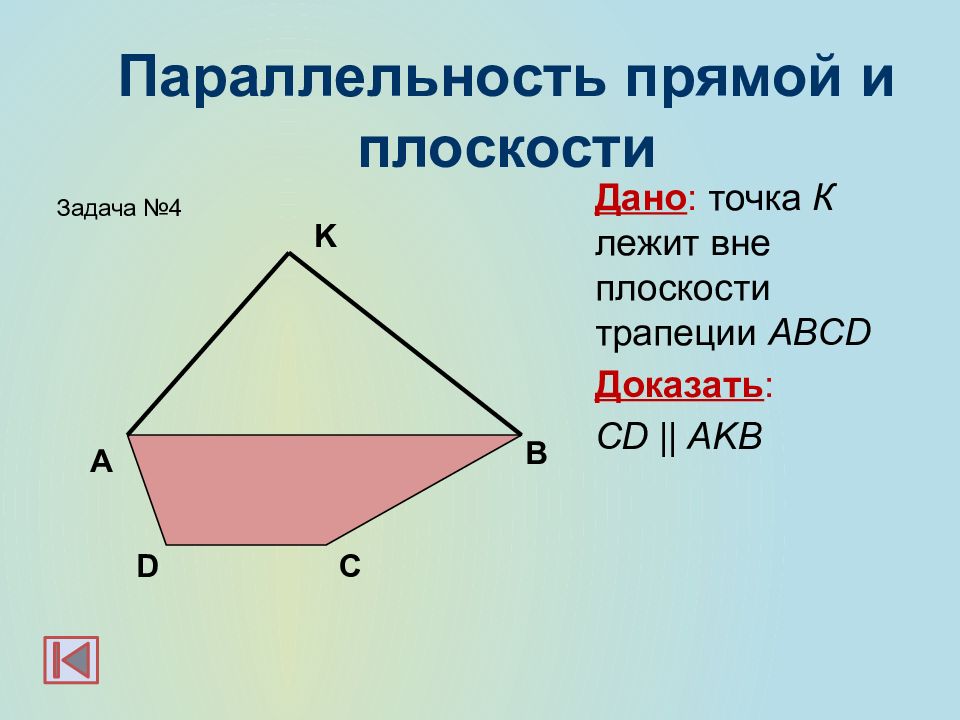
Дано : точка К лежит вне плоскости трапеции ABCD Доказать : CD || AKB K В А С D Задача №4
Слайд 12: Параллельность прямой и плоскости
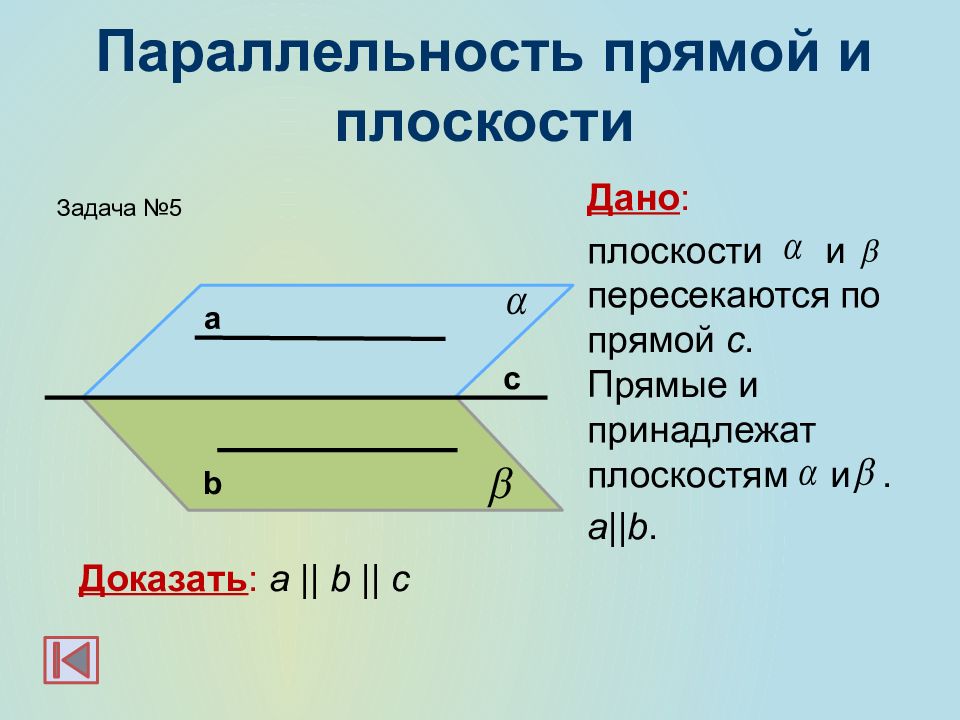
Дано : плоскости и пересекаются по прямой с. Прямые и принадлежат плоскостям и. a||b. Доказать : a || b || c а b c Задача №5
Слайд 13: Параллельность прямой и плоскости
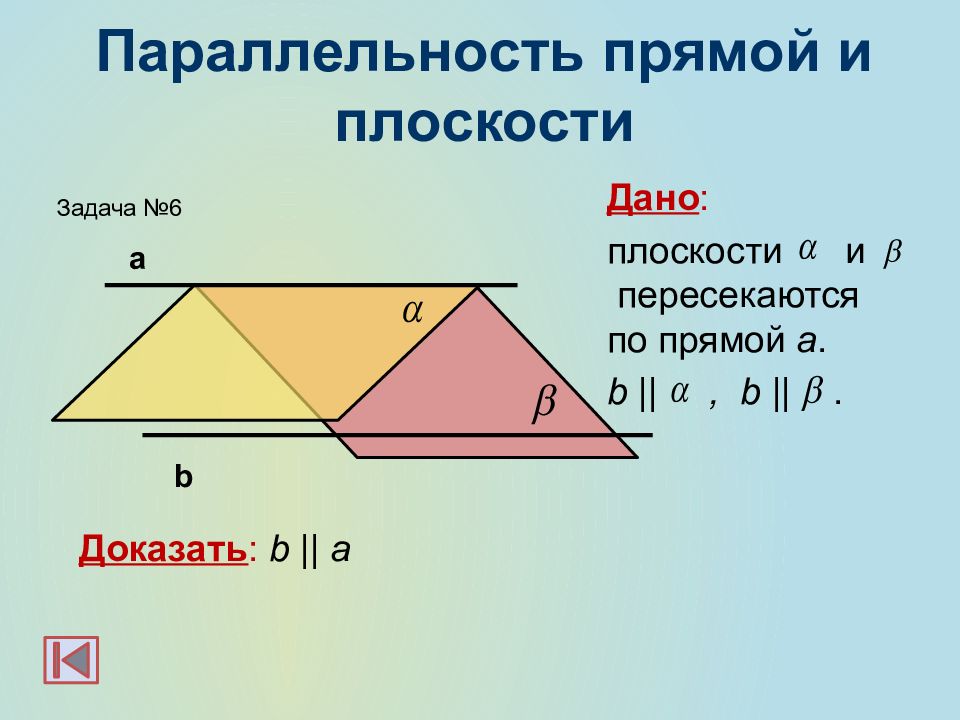
Дано : плоскости и пересекаются по прямой а. b ||, b ||. Доказать : b || a а b Задача №6
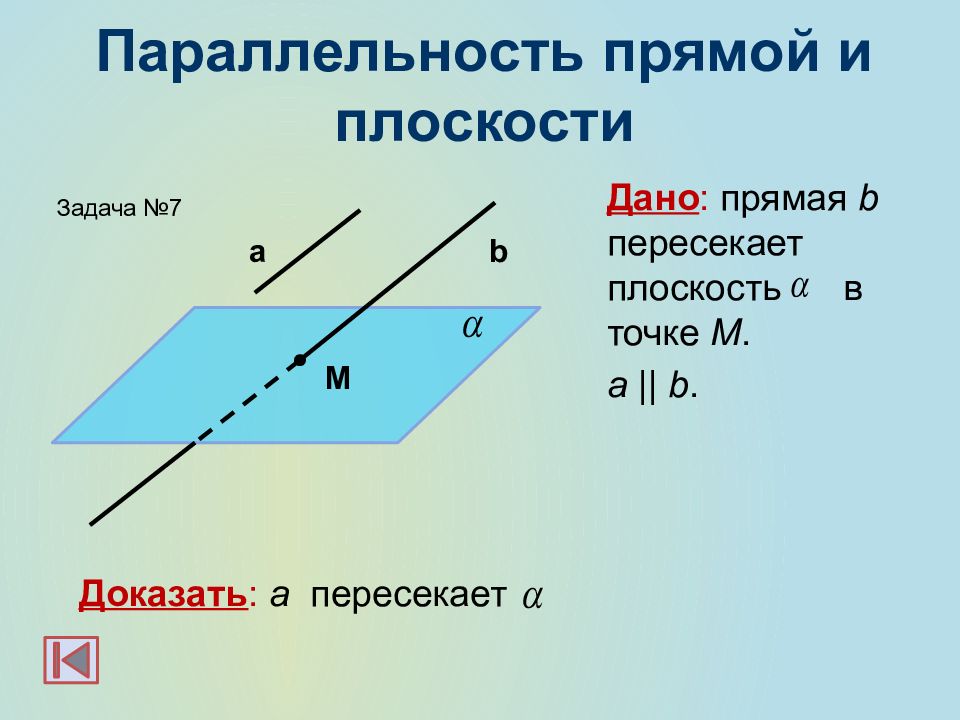
Слайд 14: Параллельность прямой и плоскости
Дано : прямая b пересекает плоскость в точке M. а || b. Доказать : a пересекает а b M Задача №7
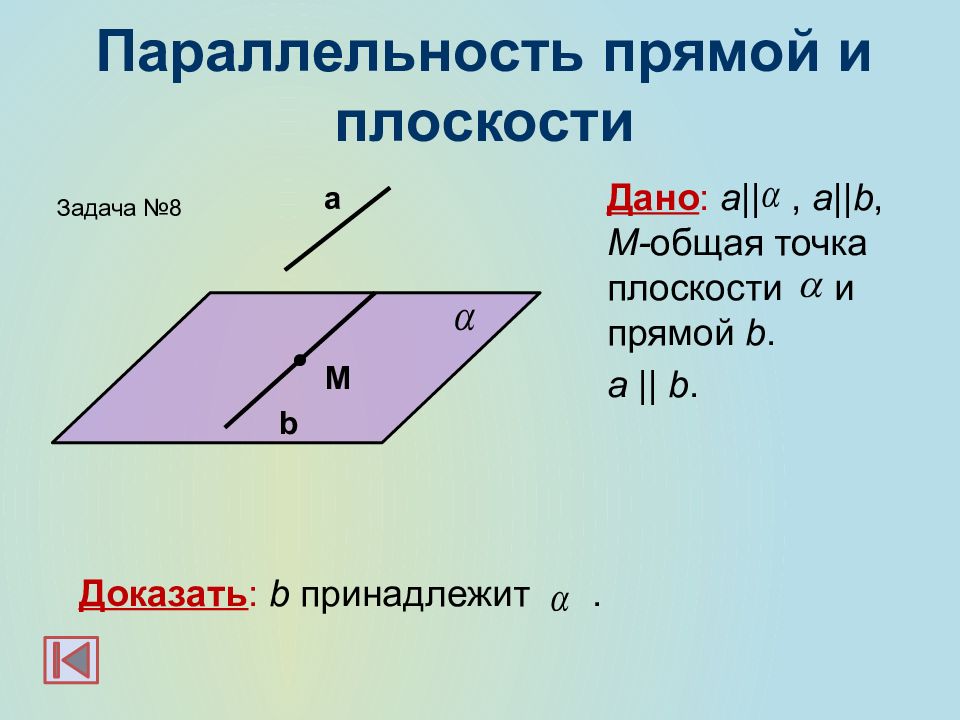
Слайд 15: Параллельность прямой и плоскости
Дано : а ||, a||b, M- общая точка плоскости и прямой b. а || b. Доказать : b принадлежит. а M b Задача №8
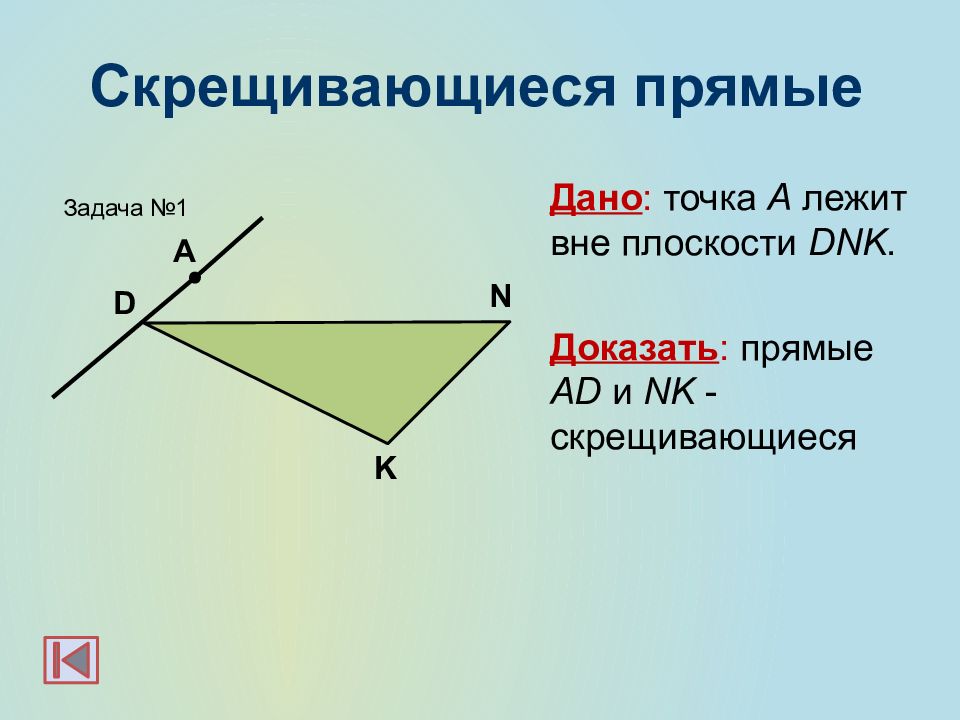
Слайд 16: Скрещивающиеся прямые
Дано : точка А лежит вне плоскости DNK. Доказать : прямые AD и NK - скрещивающиеся А K N D Задача №1
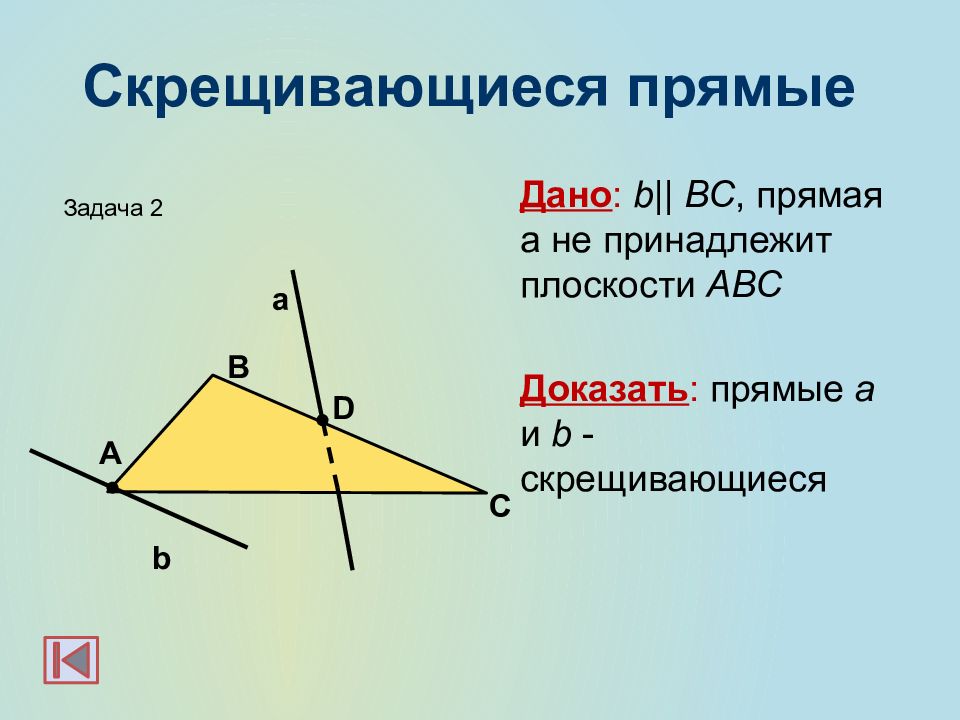
Слайд 17: Скрещивающиеся прямые
Дано : b|| BC, прямая а не принадлежит плоскости АВС Доказать : прямые a и b - скрещивающиеся b а А С В D Задача 2
Слайд 18: Скрещивающиеся прямые
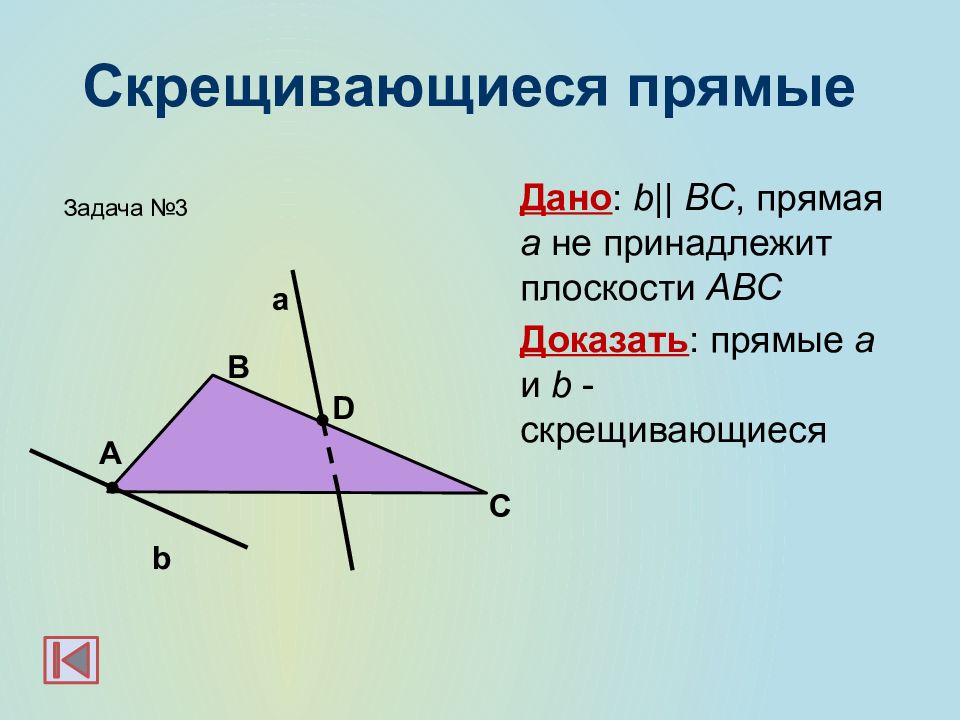
Дано : b|| BC, прямая а не принадлежит плоскости АВС Доказать : прямые a и b - скрещивающиеся b а А С В D Задача №3
Слайд 19
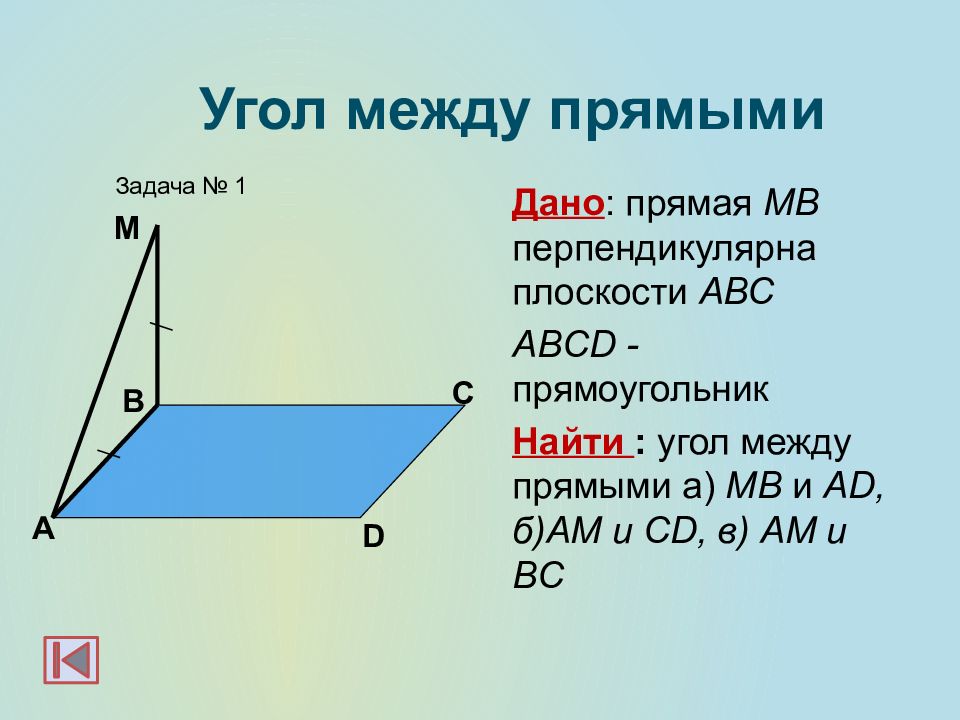
Дано : прямая МВ перпендикулярна плоскости АВС ABCD - прямоугольник Найти : угол между прямыми а) МВ и AD, б) AM и CD, в) AM и BC А B Задача № 1 М Угол между прямыми D C
Слайд 20
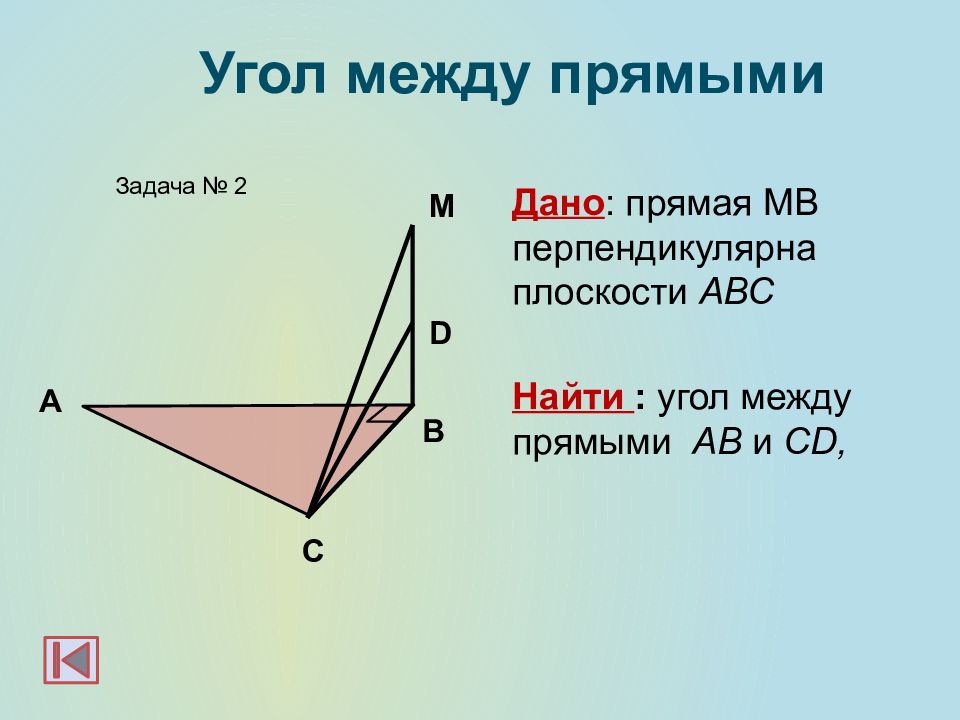
А B Задача № 2 М Угол между прямыми D C Дано : прямая МВ перпендикулярна плоскости АВС Найти : угол между прямыми АВ и С D,
Слайд 21
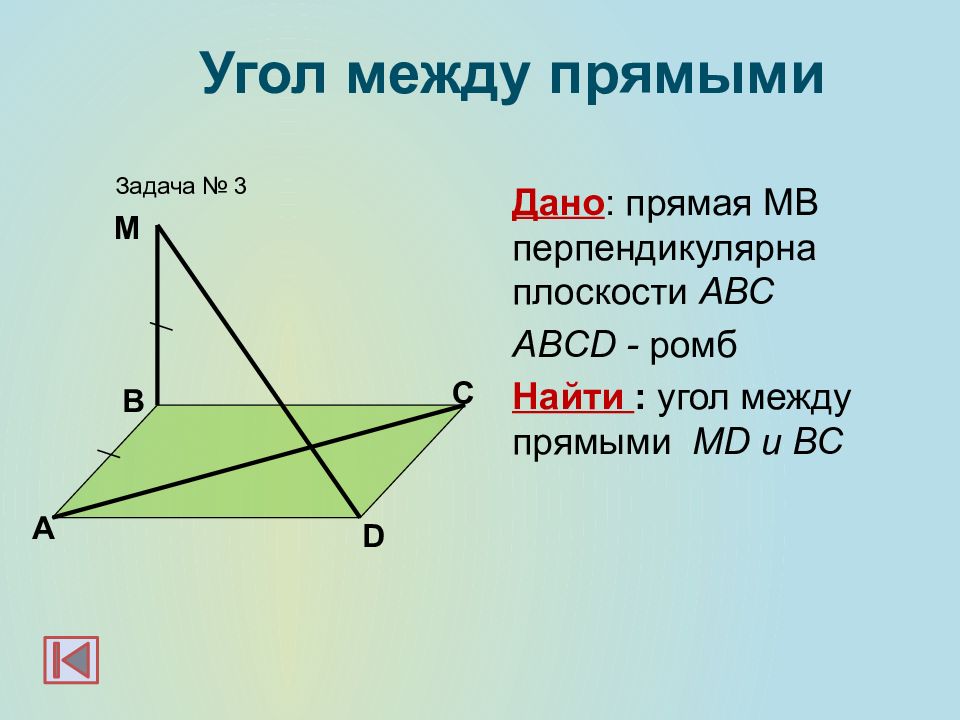
Дано : прямая МВ перпендикулярна плоскости АВС ABCD - ромб Найти : угол между прямыми М D и BC А B Задача № 3 М Угол между прямыми D C
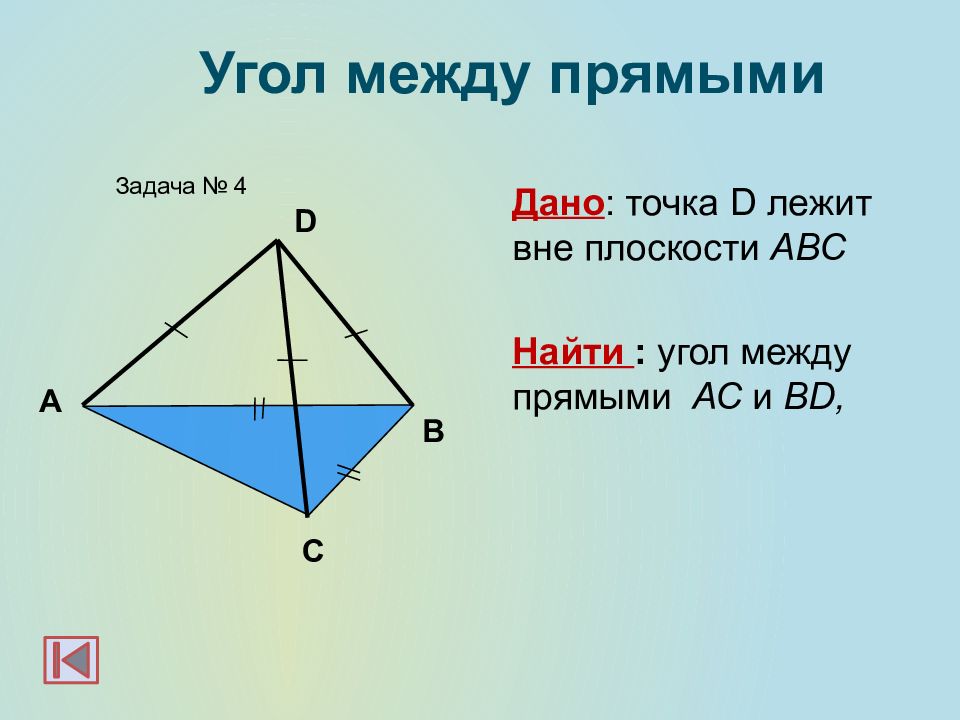
Слайд 22
А B Задача № 4 Угол между прямыми D C Дано : точка D лежит вне плоскости АВС Найти : угол между прямыми АС и В D,
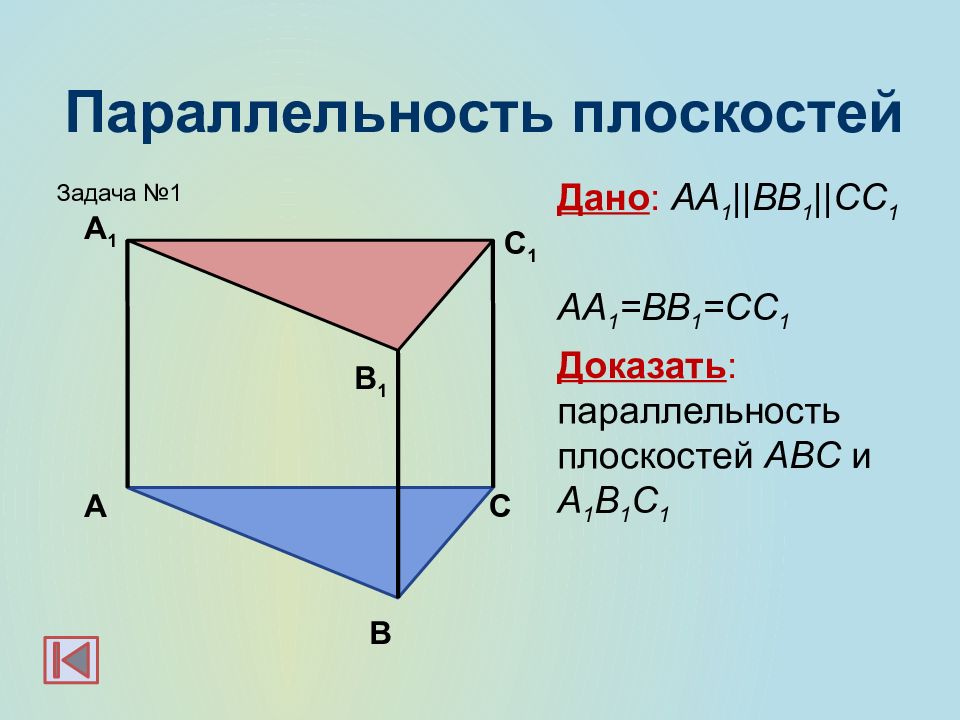
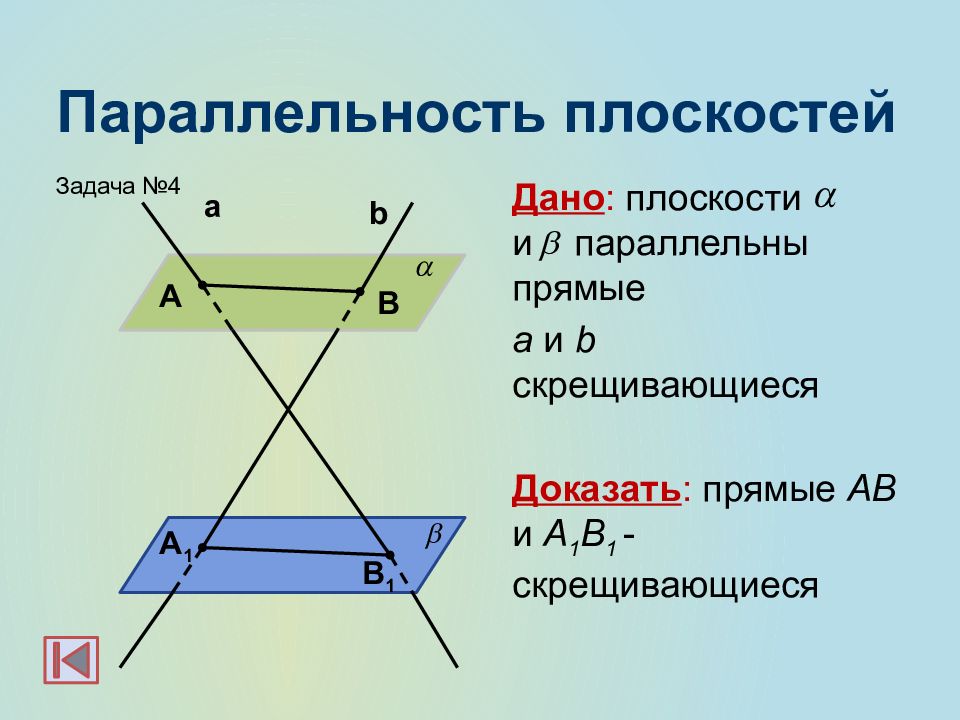
Слайд 23: Параллельность плоскостей
Дано : АА 1 ||BB 1 ||CC 1 АА 1 =BB 1 =CC 1 Доказать : параллельность плоскостей А BC и А 1 B 1 C 1 А С 1 В А 1 С В 1 Задача №1
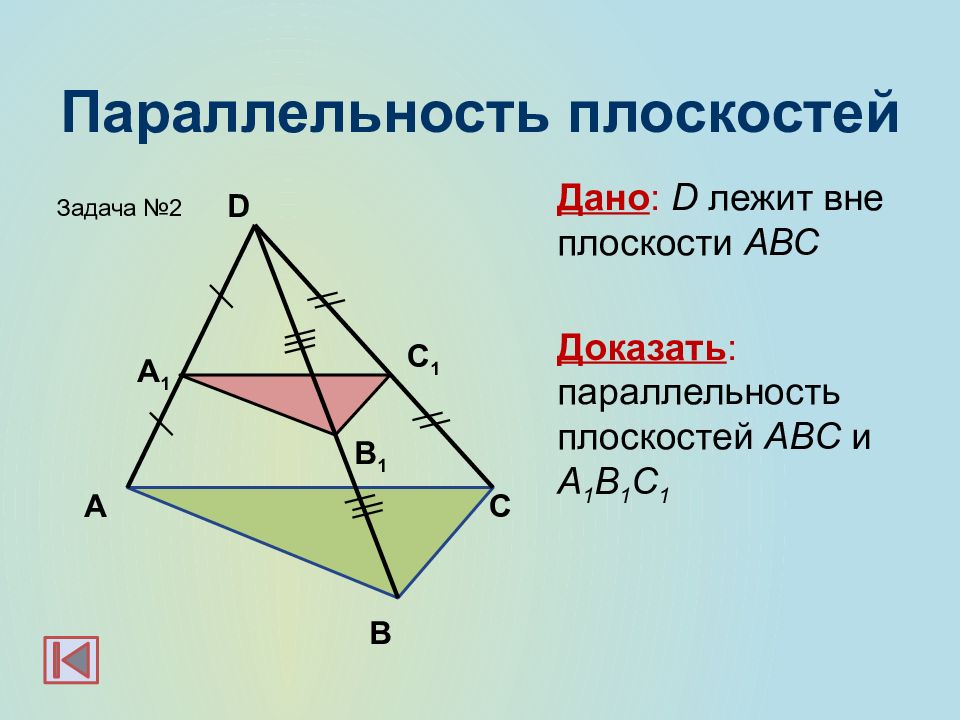
Слайд 24: Параллельность плоскостей
Дано : D лежит вне плоскости АВС Доказать : параллельность плоскостей А BC и А 1 B 1 C 1 А С 1 В А 1 С В 1 D Задача №2
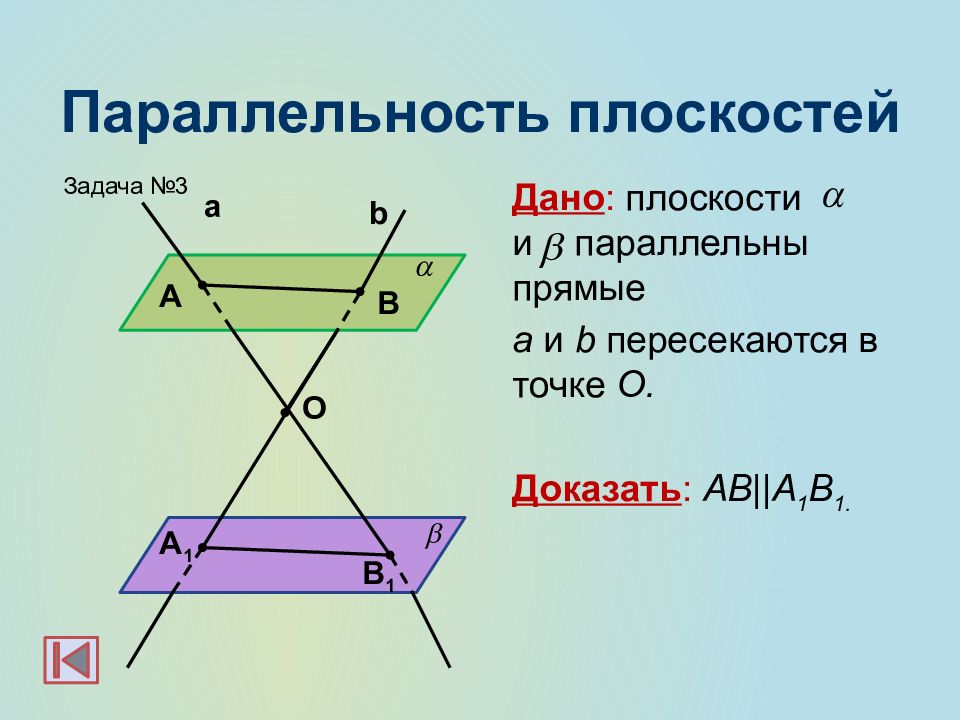
Слайд 25: Параллельность плоскостей
Дано : плоскости и параллельны прямые а и b пересекаются в точке О. Доказать : АВ || А 1 В 1. b а А В А 1 В 1 O Задача №3