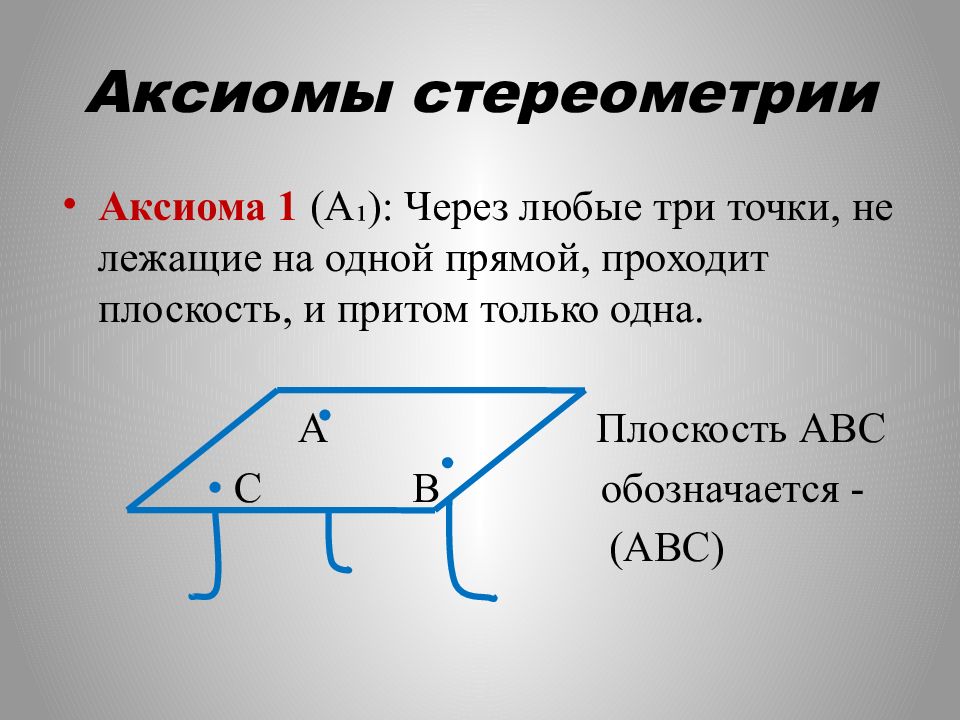
Аксиома 1 (А₁): Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А Плоскость АВС С В обозначается - (АВС)
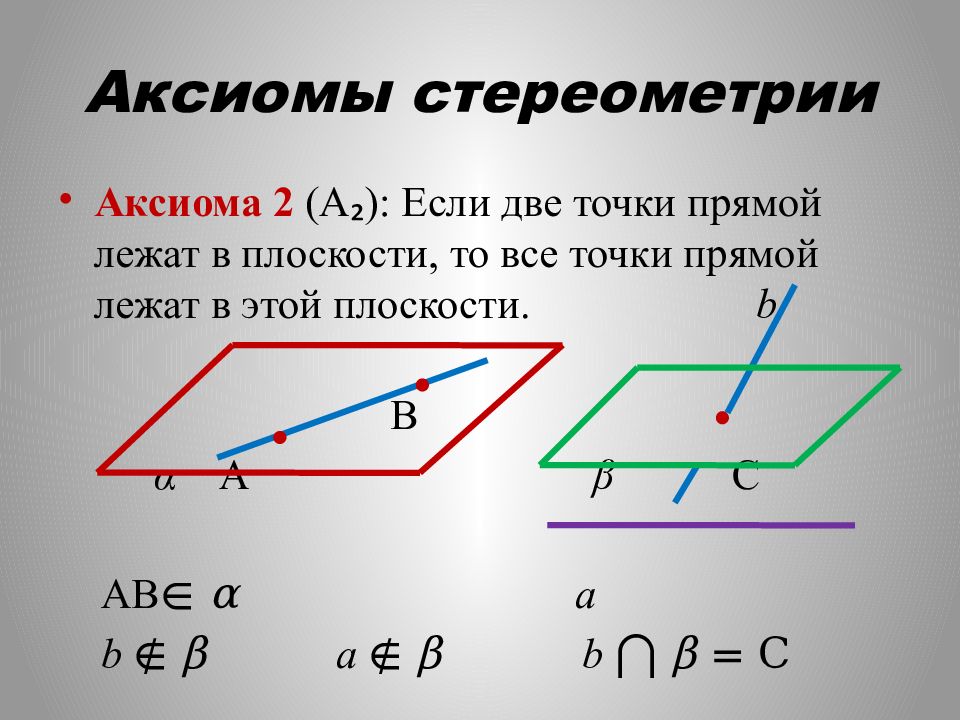
Аксиома 2 (А ₂ ): Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. b В α А β С АВ ∈ α a b ∉ β a ∉ β b ⋂ β = C
Аксиома 3 (А ₃ ): Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. β А a α α ⋂ β = a
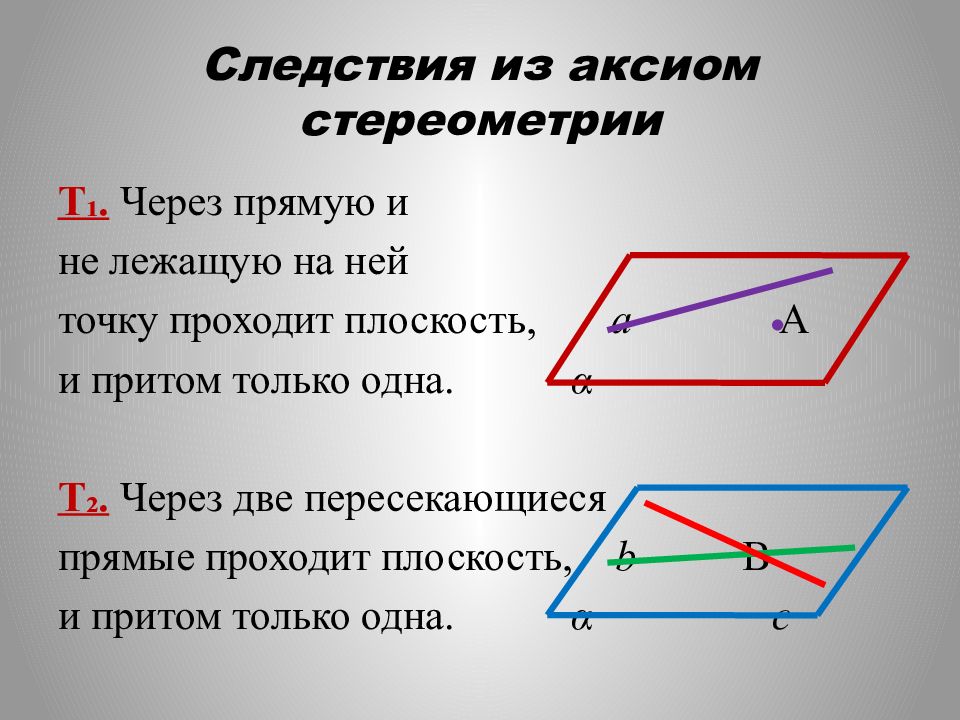
Т₁. Через прямую и не лежащую на ней точку проходит плоскость, a А и притом только одна. α Т₂. Через две пересекающиеся прямые проходит плоскость, b В и притом только одна. α c
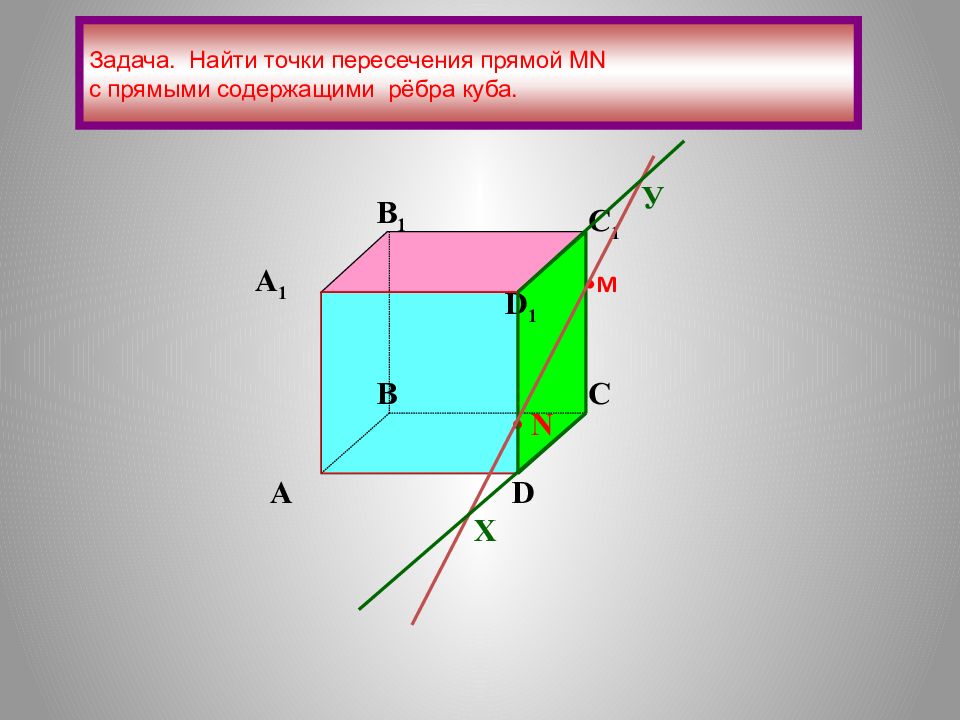
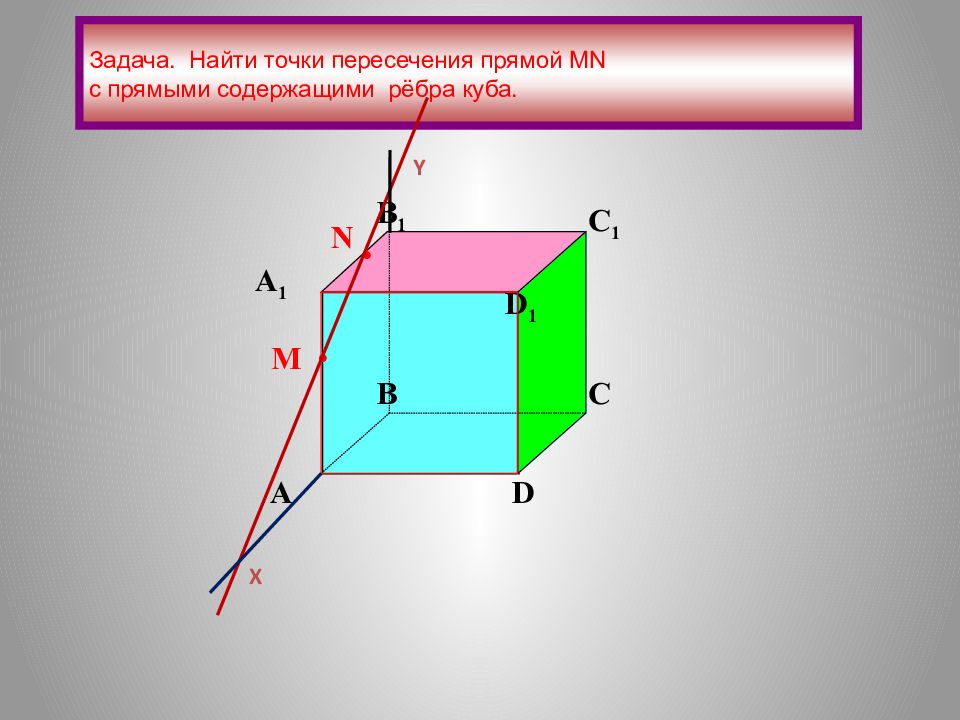
A 1 A B B 1 C 1 C D 1 D M N Задача. Найти точки пересечения прямой М N с прямыми содержащими рёбра куба. Х Y • •
Задача. Найти точки пересечения прямой М N с прямыми содержащими рёбра куба. A 1 A B B 1 C 1 C D 1 D • N • M Х У
A 1 A B B 1 C 1 C D 1 D • • M N Задача. Найти точки пересечения прямой М N с прямыми содержащими рёбра куба. Х Y
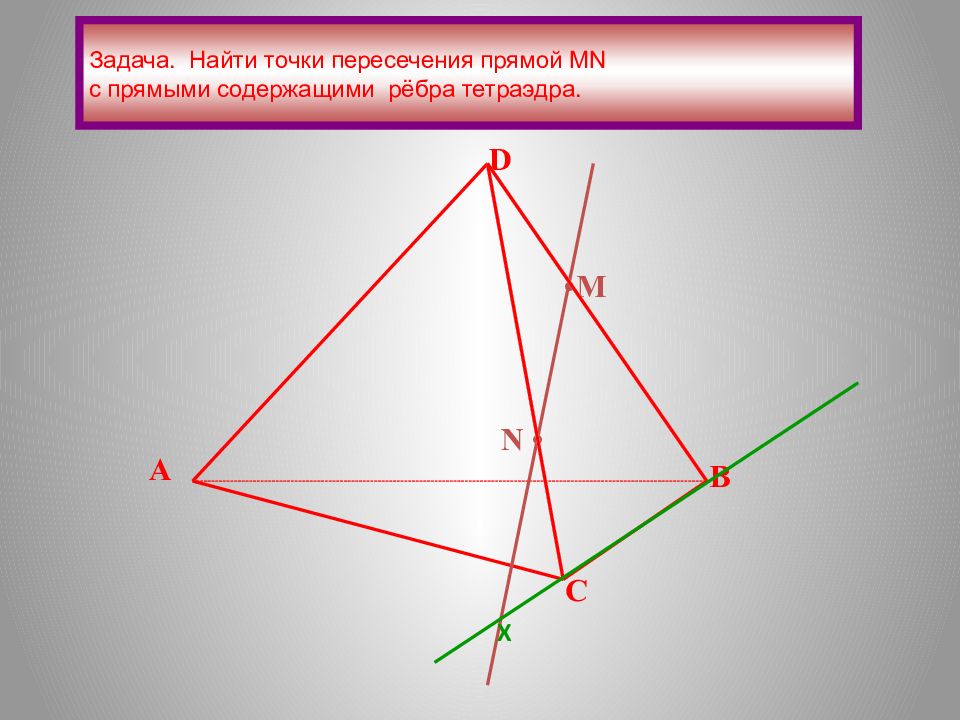
Задача. Найти точки пересечения прямой М N с прямыми содержащими рёбра тетраэдра. А В С D • М N • X
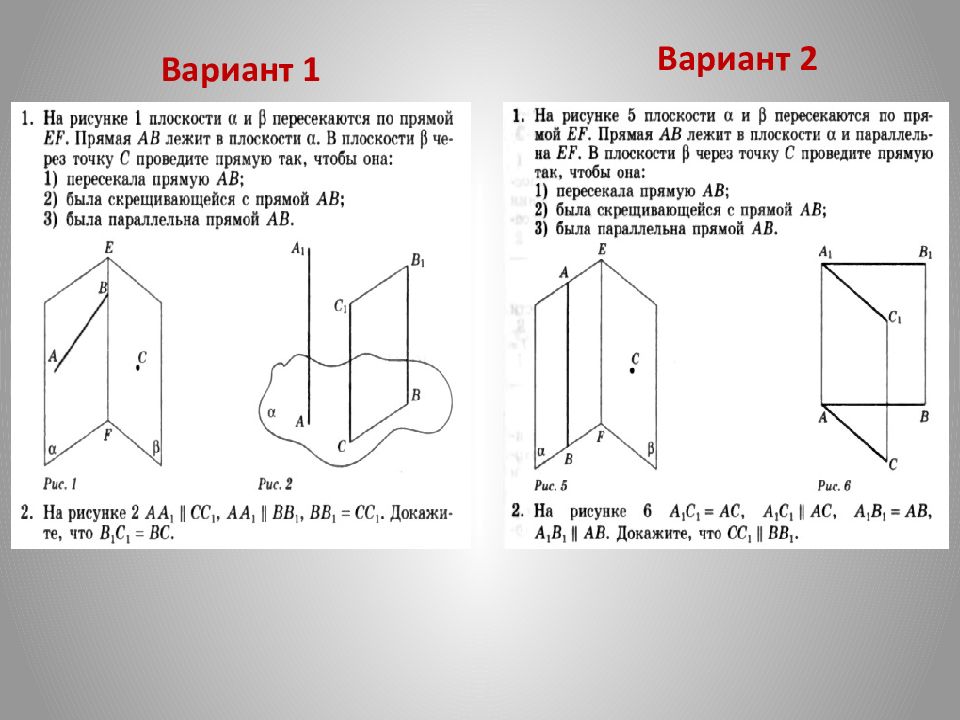
Вариант 1 1. Назовите и изобразите основные фигуры на плоскости. 2. Сформулируйте аксиому А₂. 3. Могут ли прямая и плоскость иметь две общие точки? 4. Сколько плоскостей можно провести через три точки? 5. Сколько может быть общих точек у прямой и плоскости? Вариант 2 1. Назовите и изобразите основные фигуры в пространстве. 2. Сформулируйте аксиому А ₁. 3. Сколько плоскостей можно провести через прямую и не лежащую на ней точку? 4. Сформулируйте аксиому А ₃. 5. Могут ли прямая и плоскость иметь одну общую точку?
Вариант 1 Вариант 2
Вариант 1 Вариант 2
