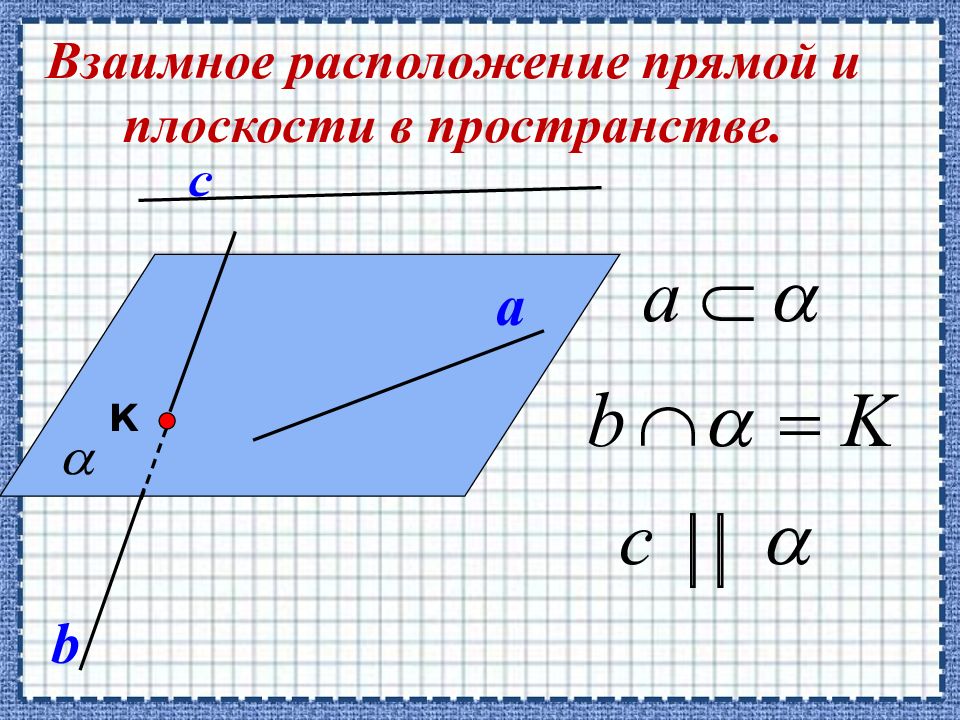
Взаимное расположение прямых и плоскостей в пространстве
Все построения на плоскости производятся чертежными инструментами и построения получаются точными, а вот выполнять построения в пространстве можно схематически. Поэтому термины «провести плоскость (прямую)» употребляют в смысле «доказать существование плоскости (прямой)», удовлетворяющей поставленным условиям.
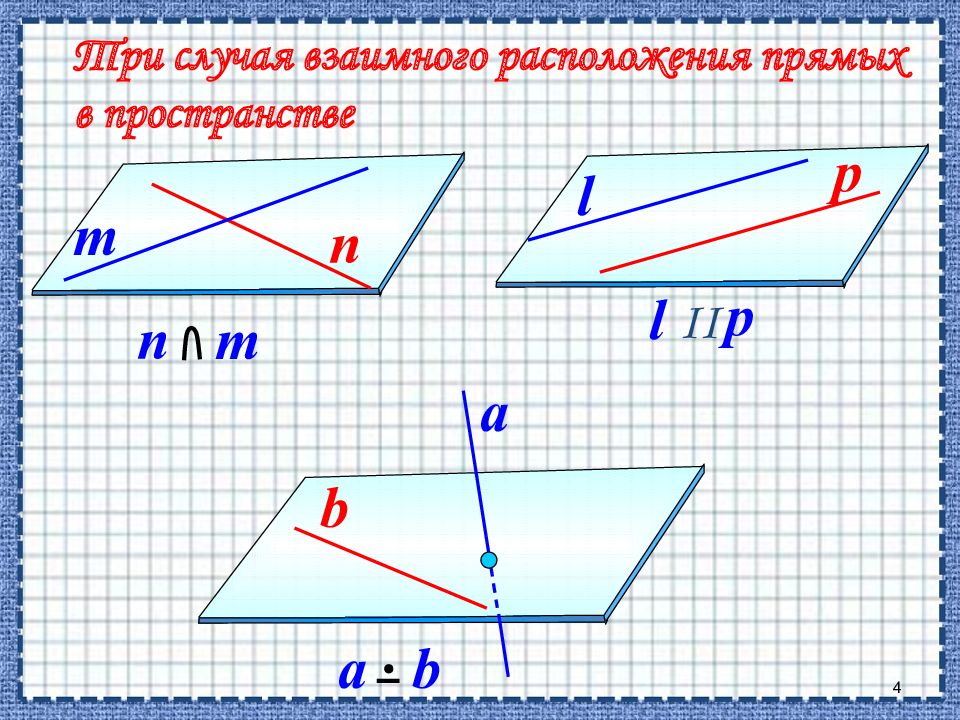
4 b a b Три случая взаимного расположения прямых в пространстве n m l p n m l p II a
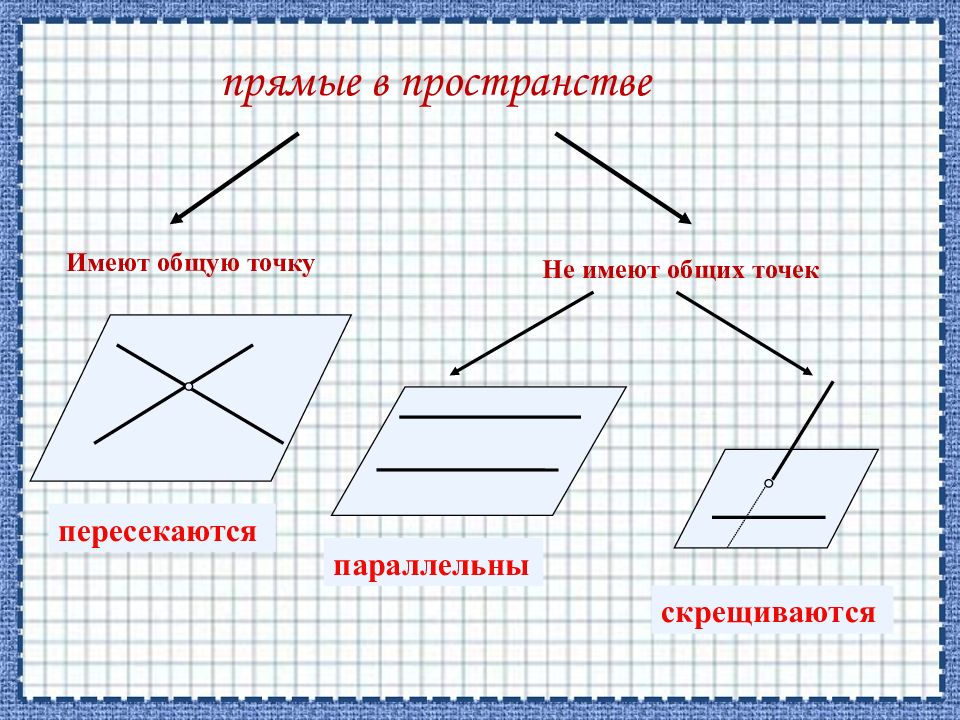
прямые в пространстве Имеют общую точку Не имеют общих точек пересекаются параллельны скрещиваются
Определение: Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общей точки или совпадают. Определение: Две прямые называются скрещивающимися, если они не пересекаются и не параллельны. Определение: Две прямые называются пересекающимися, если они лежат в одной плоскости и имеют одну общую точку.
Дано: К a Доказать: ! b : К b, b a Доказательство: Построение 1.Проведем через прямую a и т. К плоскость α. (по Сл.1) 2.Проведем через т. К в плоскости α прямую b, b a.(А планиметрии) Единственность (от противного) 1.Пусть b 1 : К b 1, b 1 a.Через прямые a и b 1 можно провести плоскость α 1 (по Сл.3) 2. Прямая a, т.К α 1 ; α 1 = α (по точке и прямой в пространстве) (СЛ.1). 3. b = b 1 (А параллельных прямых). Теорема доказана. К a b
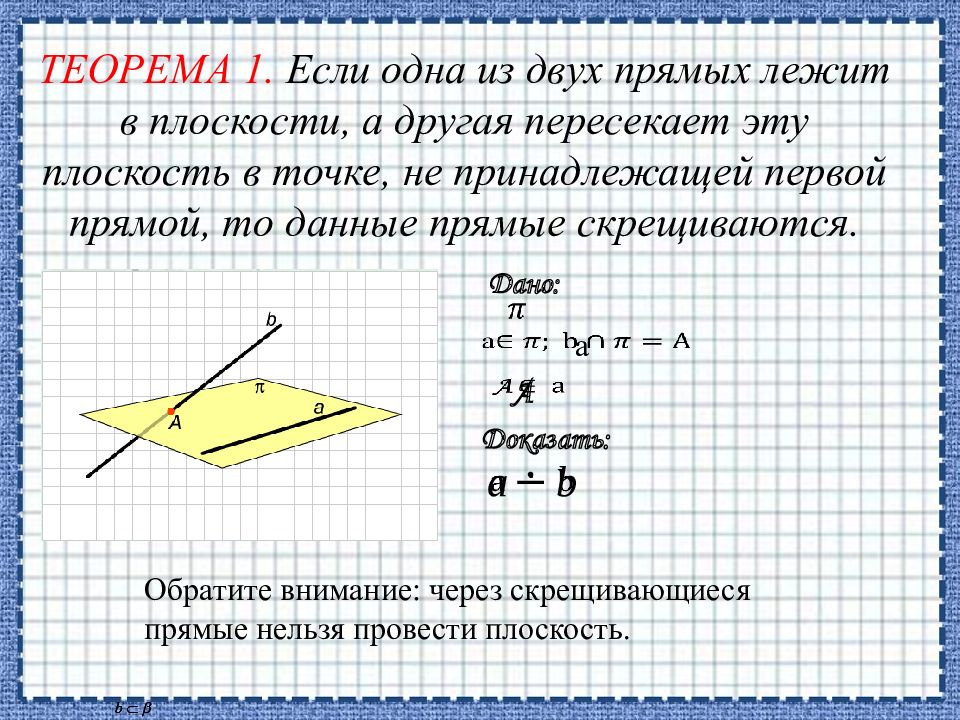
ТЕОРЕМА 1. Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые скрещиваются. Обратите внимание: через скрещивающиеся прямые нельзя провести плоскость. Дано: Доказать: a А
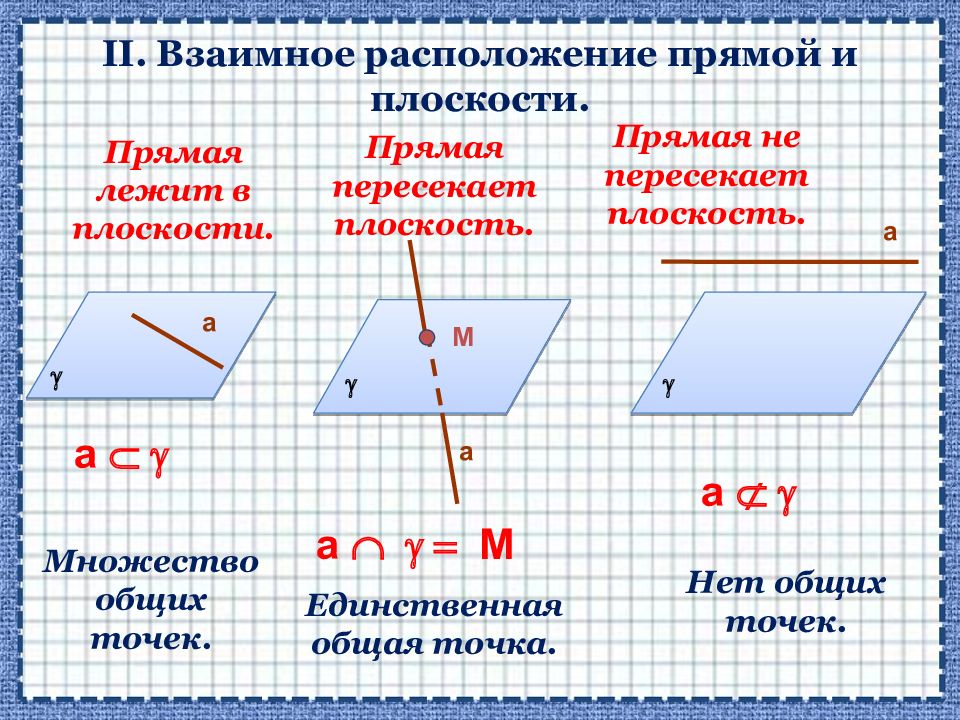
II. Взаимное расположение прямой и плоскости. Прямая лежит в плоскости. Прямая пересекает плоскость. Прямая не пересекает плоскость. Множество общих точек. Единственная общая точка. Нет общих точек. g а g а М g а а Ì g а Ç g = М а Ë g
a с Взаимное расположение прямой и плоскости в пространстве. b К
Определение. Прямая и плоскость называются параллельными, если они не имеют общей точки или прямая лежит в плоскости. Рассмотрим следующий признак параллельности прямой и плоскости
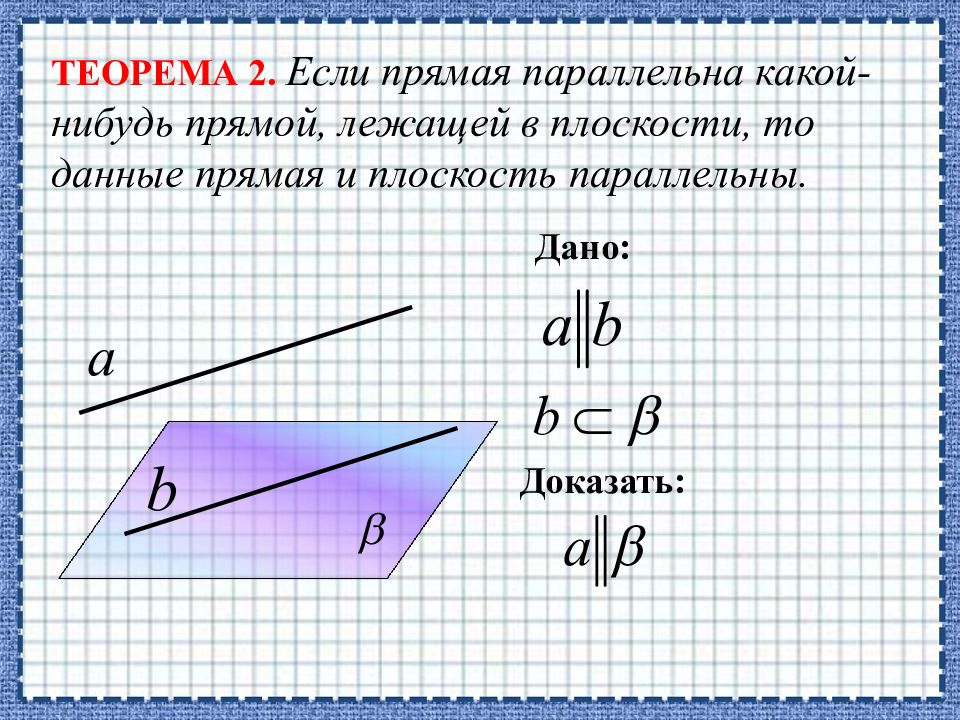
ТЕОРЕМА 2. Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то данные прямая и плоскость параллельны. Дано: Доказать:
ТЕОРЕМА 3 (обратная) Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Дано: β ∩ α = Доказать: Доказательство: 1) а, b β а не может ∩ b, так как иначе а ∩ α, что противоречит условию. Следовательно а в α Теорема доказана.
ТЕОРЕМА 4. Если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то их линия пересечения параллельна каждой из данных прямых. Дано: Доказательство: Доказать: а b α β = с с а, c b α Через а проведена α, через b – β, причем α ∩ β = с По признаку || прямой и плоскости а || β, тогда с а (Т.3) Аналогично доказывается с|| b
Доказательство: Рассмотрим случай. в, с β; а, с α 1. Возьмем т.М, М а Через т.М и с проведем плоскость α, b и М проведем плоскость β; 2. Т 4 : α β = MN (линия пересечения плоскостей b и с) 3. Через т.М нельзя провести двух различных прямых с, поэтому MN и а совпадают. 4. Но так как ( MN ) b, то и а b в с Теорема доказана. Теорема 5. Если две прямые параллельны третьей, то они параллельны между собой. Дано: а с, b c Доказать: а b α М N
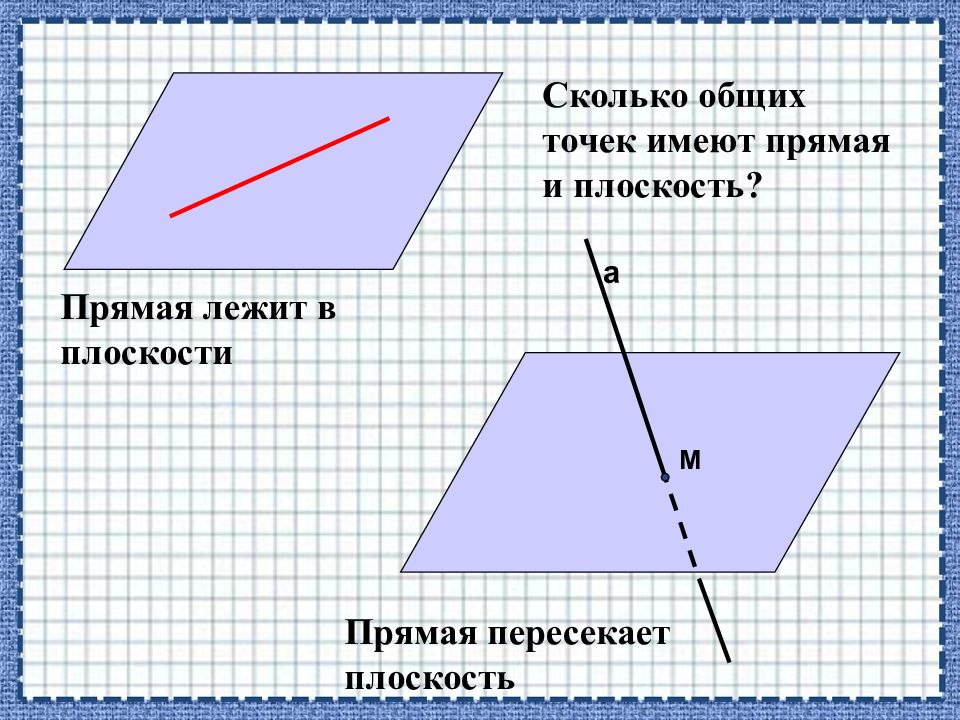
а М Прямая лежит в плоскости Прямая пересекает плоскость Сколько общих точек имеют прямая и плоскость?
Способы задания плоскостей Рисунок Как в пространстве можно однозначно задать плоскость? 1. По трем точкам 2. По прямой и не принадлежащей ей точке. 3. По двум пересекающимся прямым. 4. По двум параллельным прямым.
Задание 1 Вставьте пропущенные слова Единственную плоскость можно задать через три точки, при этом они на одной прямой. 2) Если точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. 3) Две различные плоскости могут иметь только одну общую 4) Прямые являются в пространстве, если они не пересекаются и в одной плоскости. 5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке В α, то прямые а и b не лежат две прямую параллельными лежат скрещивающиеся
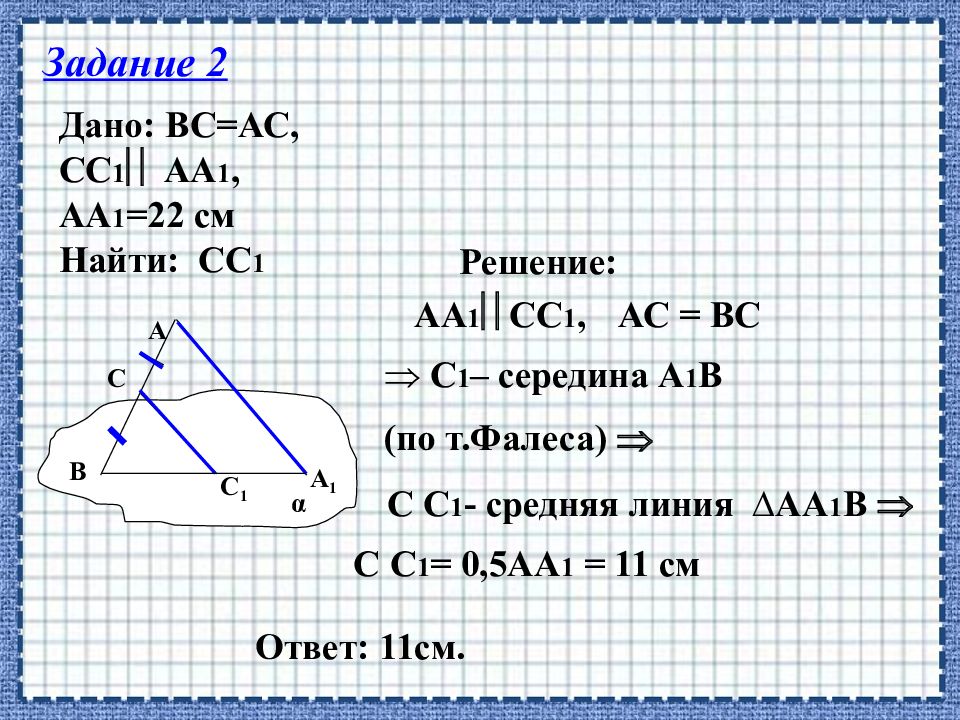
А В С С 1 А 1 α Задание 2 Дано: ВС=АС, СС 1 АА 1, АА 1 =22 см Найти: СС 1 Решение: АА 1 СС 1, АС = ВС С 1 – середина А 1 В (по т.Фалеса) С С 1 - средняя линия ∆АА 1 В С С 1 = 0,5АА 1 = 11 см Ответ: 11см.
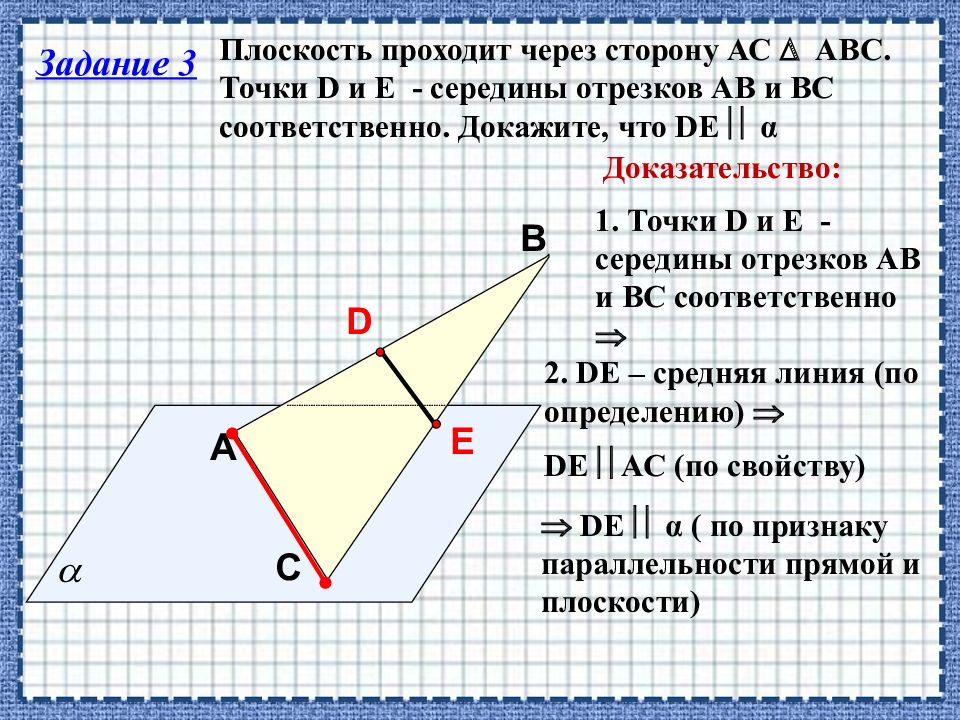
A В С Плоскость проходит через сторону АС АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE α D E Доказательство: 1. Точки D и E - середины отрезков АВ и BC соответственно 2. DE – средняя линия (по определению) DE АС (по свойству) DE α ( по признаку параллельности прямой и плоскости) Задание 3
