Первый слайд презентации: Четность и нечетность функции
Слайд 2: Свойства функций
1) Область определения функций. 2) Монотонность функции. 3) Ограниченность функции. 4) Наибольшее и наименьшее значения функции. 5) Непрерывность. 6) Область значений. 7) Выпуклость 8) Четность, нечетность.
Слайд 3
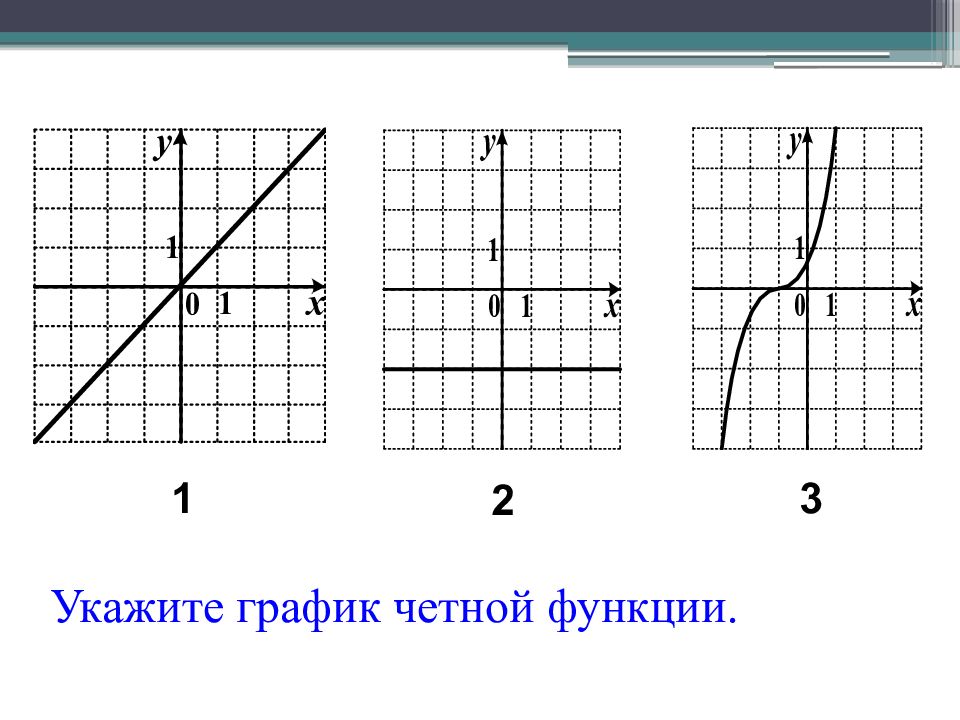
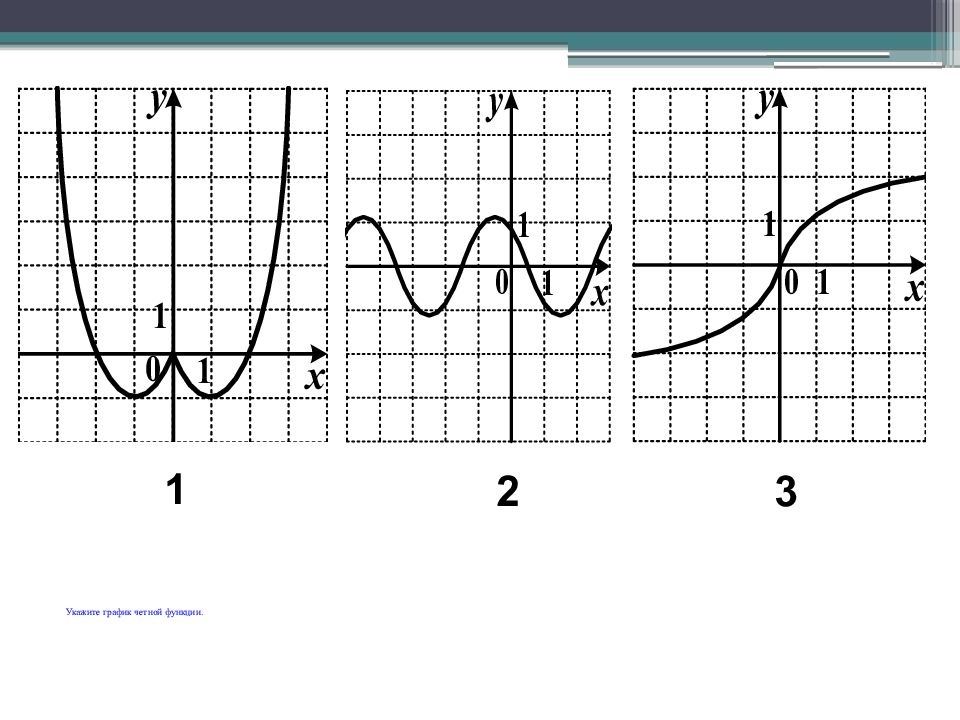
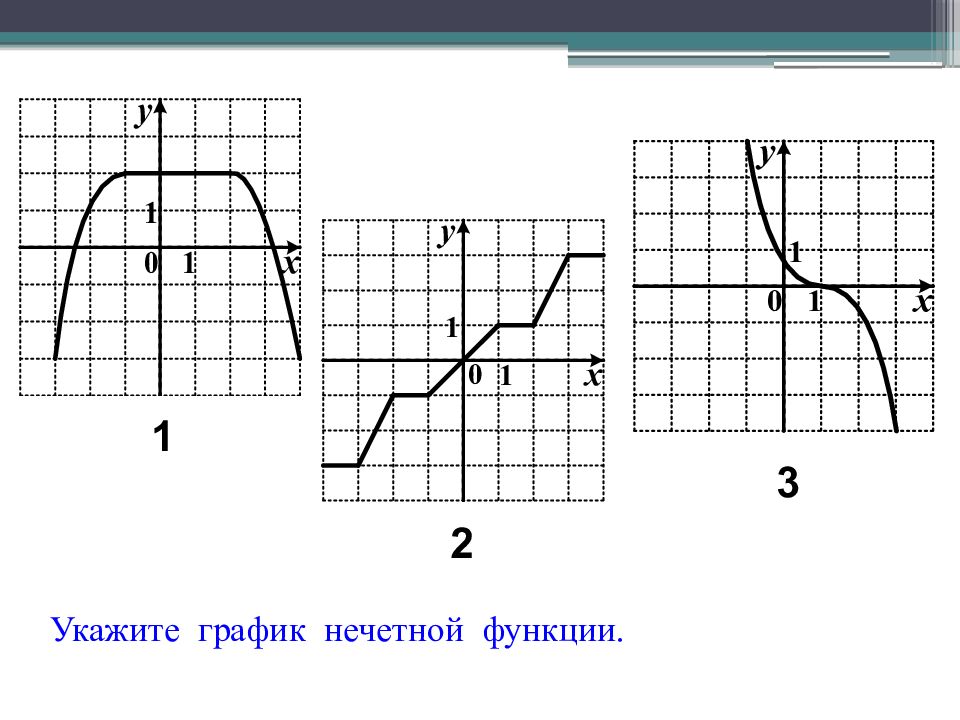
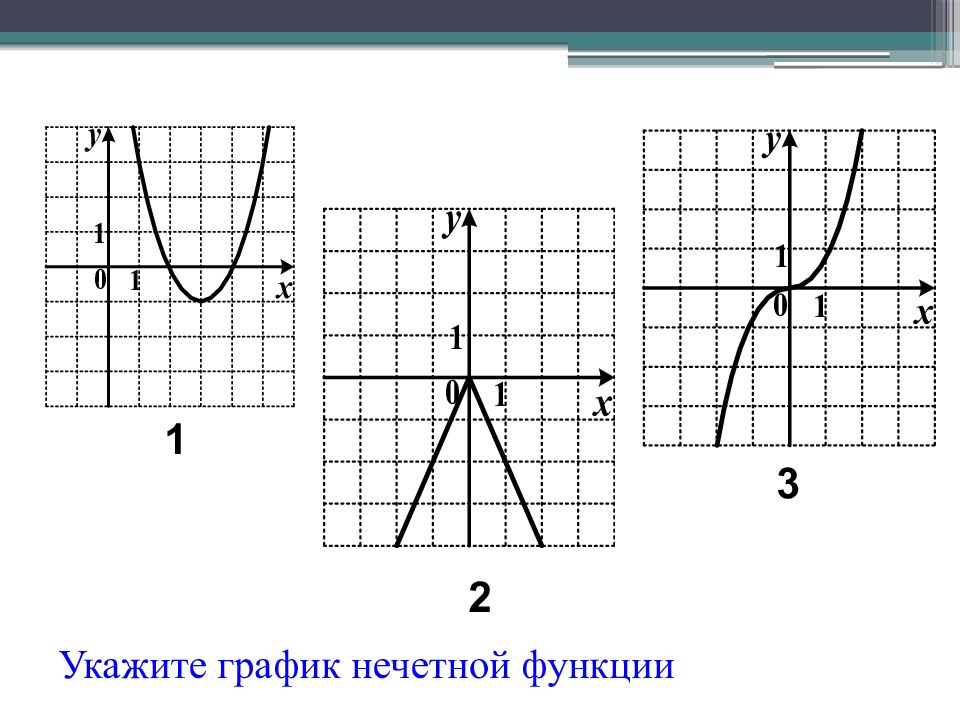
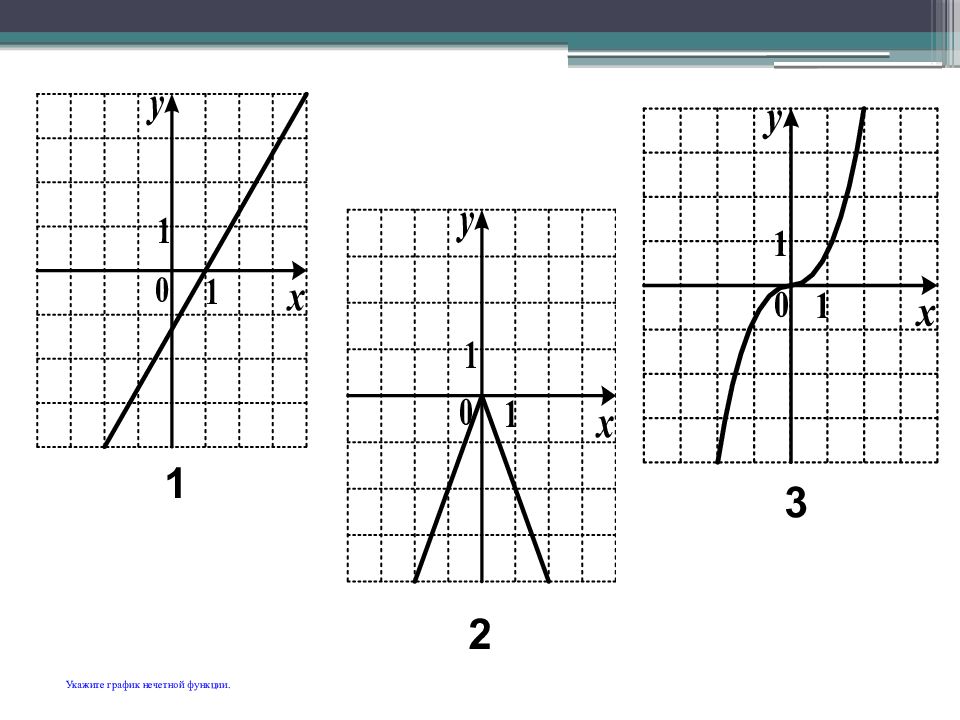
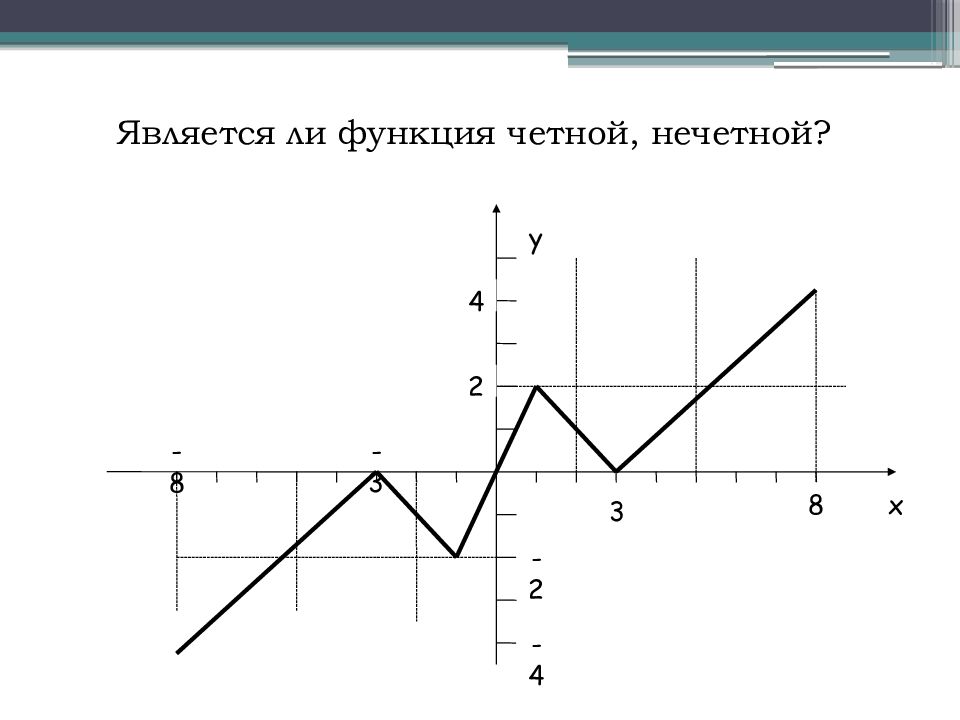
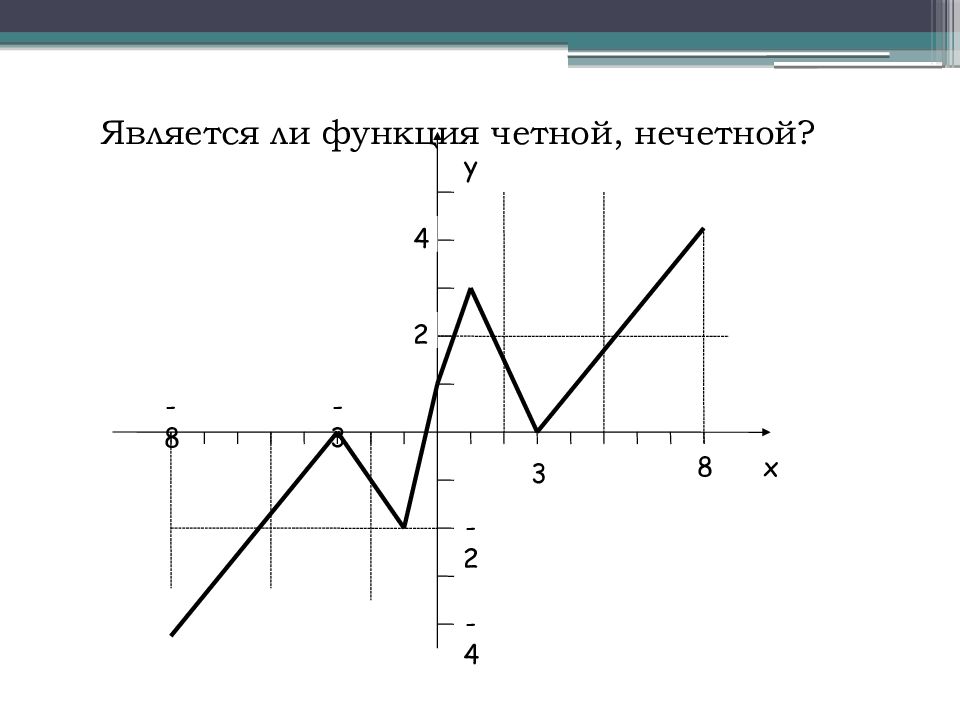
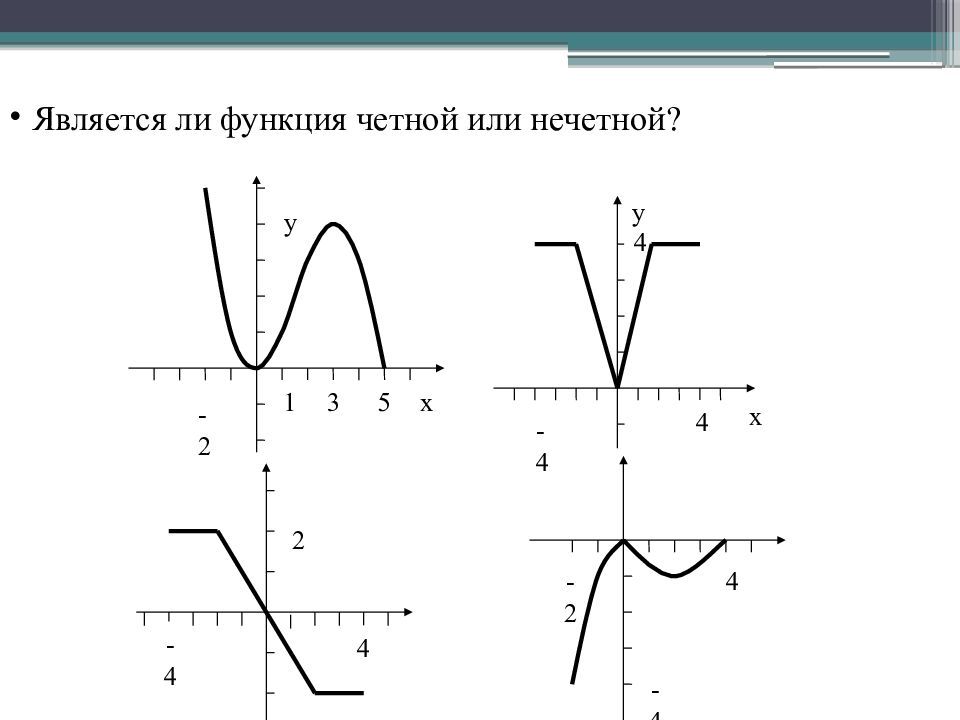
Определение: Функция y ( x ) называется четной, если область определения её симметрична относительно оси Оу и выполняется y (- x ) = y ( x ) для любого x из области определения этой функции. График четной функции симметричен относительно оси y. Определение: Функция y ( x ) называется нечетной, если область определения её симметрична относительно начала координат и выполняется y (- x ) = - y ( x ) График нечетной функции симметричен относительно начала координат.
Слайд 4
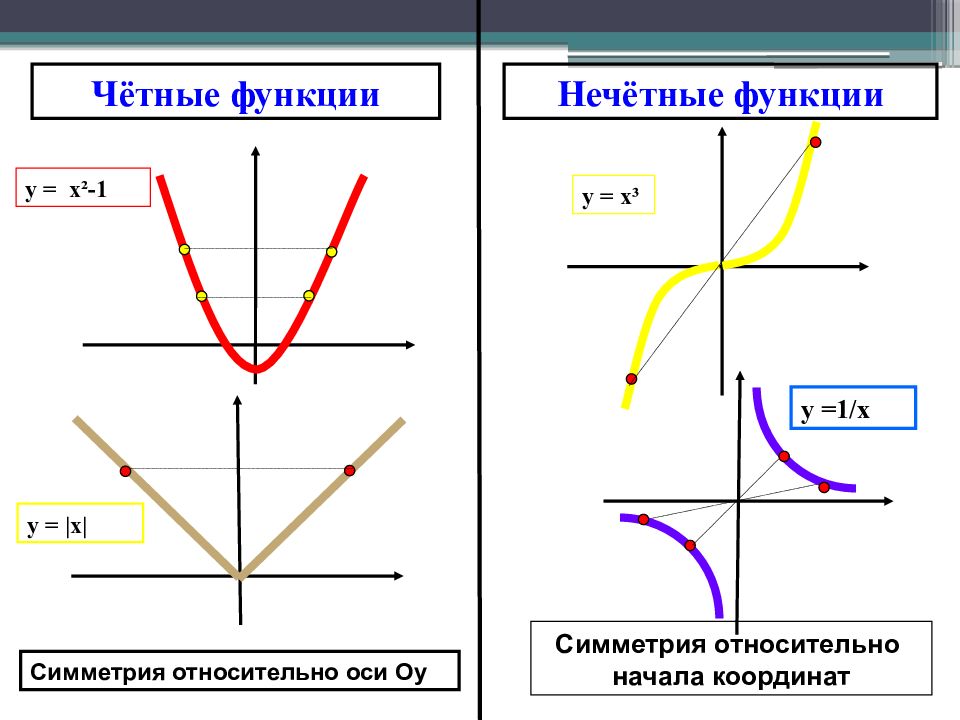
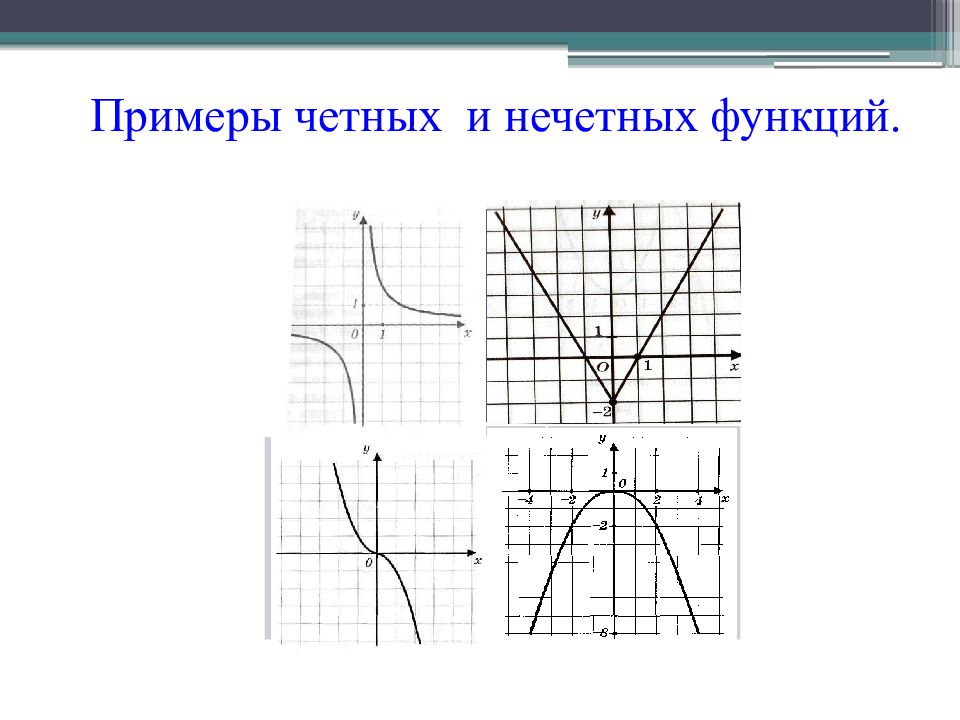
y = x² -1 y = | x | y = x ³ y = 1/х Чётные функции Нечётные функции Симметрия относительно оси О y Симметрия относительно начала координат
Установить, симметрична ли область определения функции 2 ) Найти f(-x) 3) Сравнить f(-x) и f(x)
Слайд 6
y = 7x +x ³ Решение: y (- x ) = 7( - x) + (- x) ³ = = - 7 x - x ³ = - ( 7x +x ³)= = - y ( x ) Чётные функции y ( - x) = y (x) Нечётные функции y ( - x) = - y (x) Определение Выяснить является ли функция чётной или нечётной. y = 5 x² - | X | Решение: y (- x ) = 5 • ( - x ) ² - |- x | = = 5 x ² - | x |= = y ( x ) - четная
1. f ( x ) =3 x 2 + x 4 2. f ( x ) = х(5 – x 2 ) 3. f ( x ) =4 x 6 – x 2 4. f ( x ) = x 7 +2 x 3
Слайд 8: Чётные функции
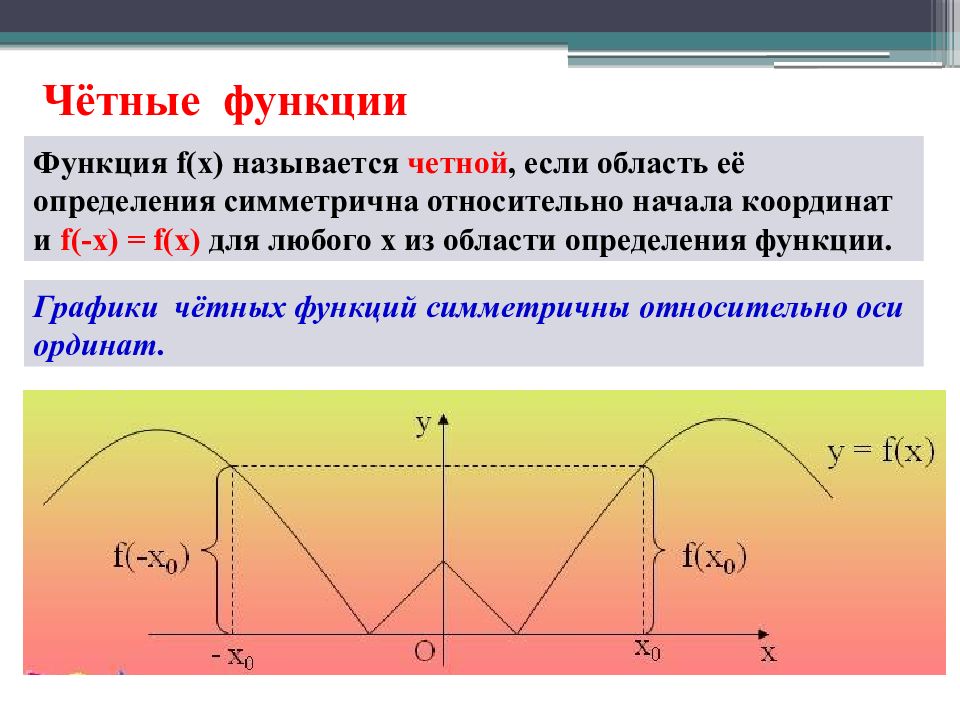
Функция f( х) называется четной, если область её определения симметрична относительно начала координат и f(-x) = f(x) для любого х из области определения функции. Графики чётных функций симметричны относительно оси ординат.
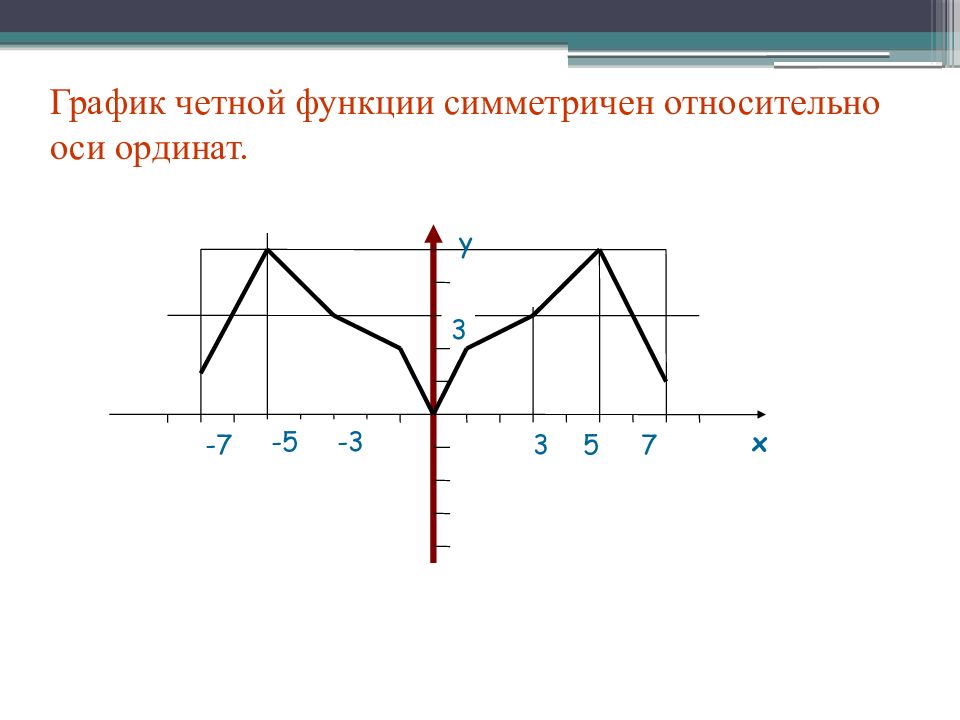
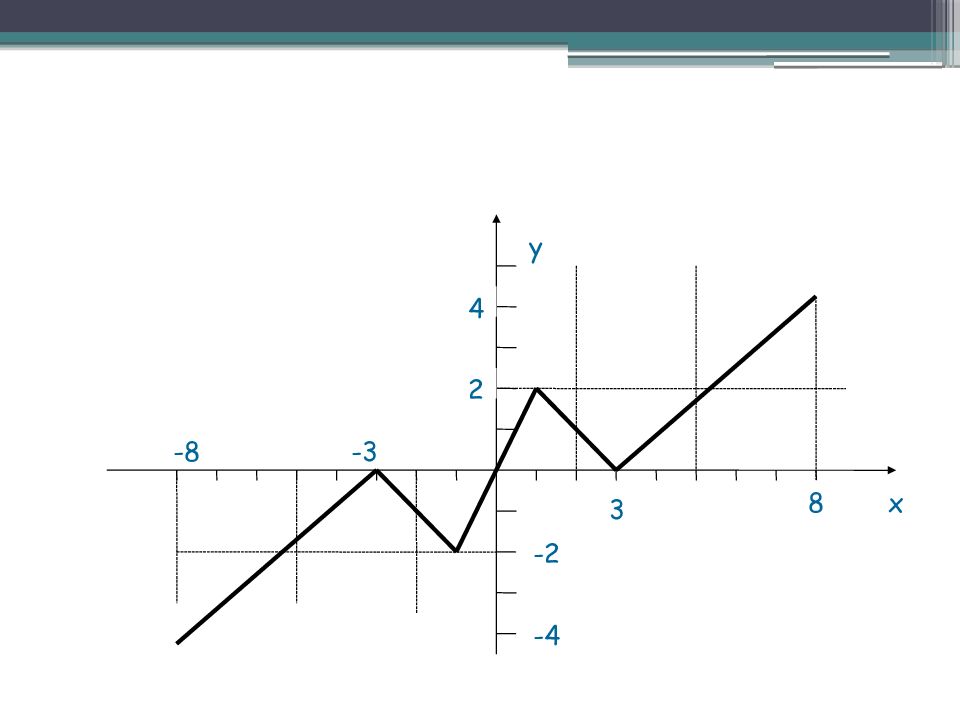
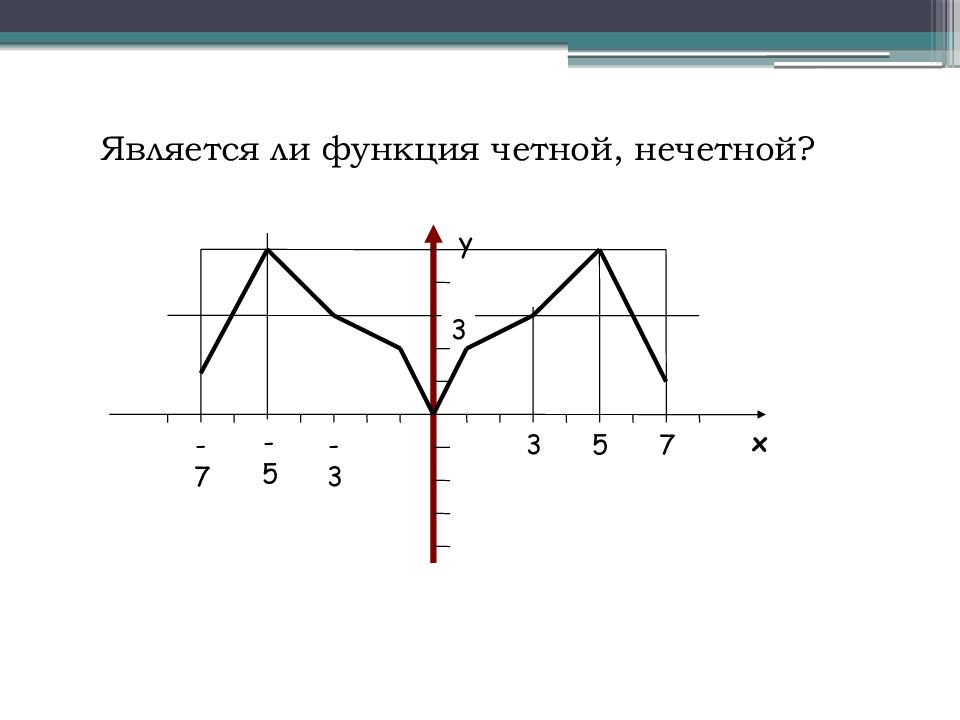
Слайд 10: График четной функции симметричен относительно оси ординат
х у -5 5 7 3 -3 -7 3
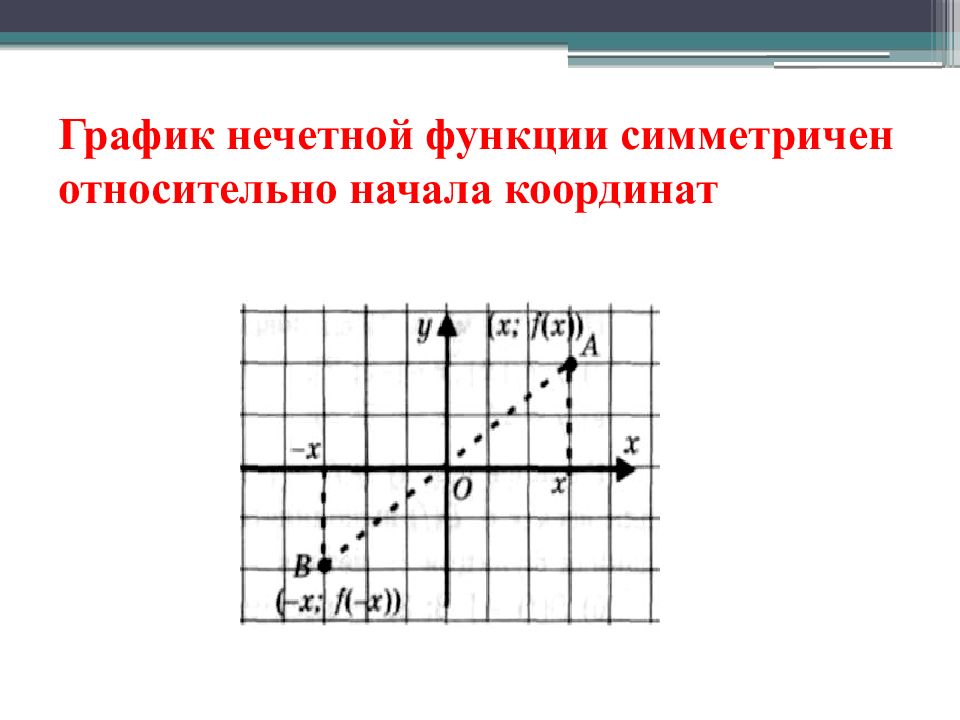
Слайд 13: Нечётные функции
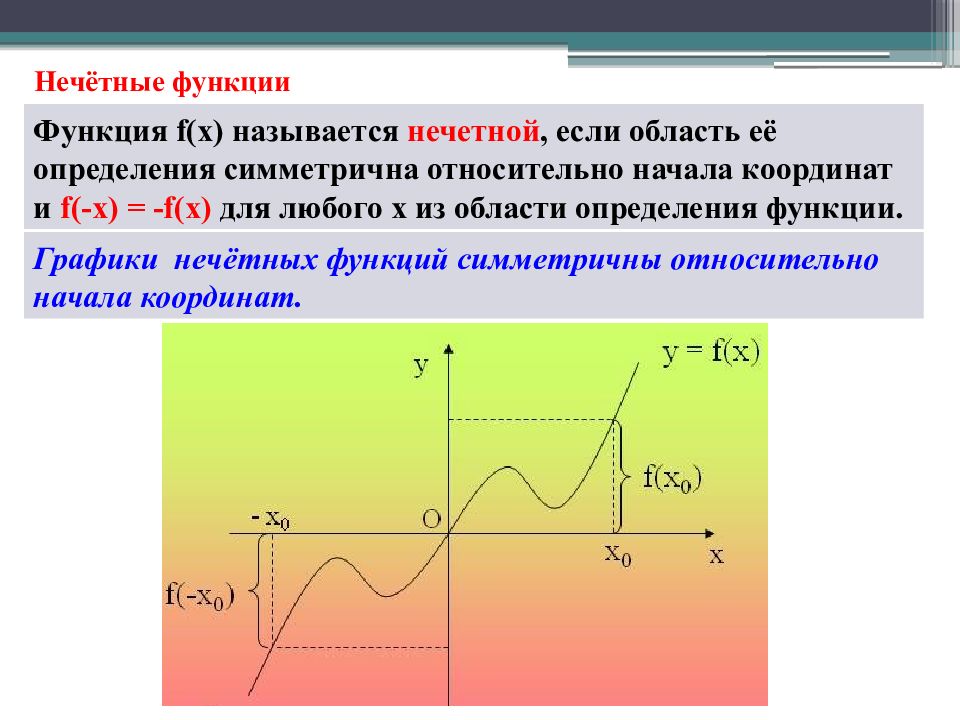
Функция f( х) называется нечетной, если область её определения симметрична относительно начала координат и f(-x) = - f(x) для любого х из области определения функции. Графики нечётных функций симметричны относительно начала координат.