Общая схема исследования функции и построения графика
Исследование функции y= f(x) целесообразно вести в определенной последовательности:
Найти область определения функции Найти (если это можно) точки пересечения графика с осями координат Найти интервалы знакопостоянства функции (промежутки, на которых f(x)>0 или f(x)<0) Выяснить, является ли функция четной, нечетной или общего вида
Найти асимптоты графика функции Найти интервалы монотонности функции Найти экстремумы функции Найти интервалы выпуклости и точки перегиба графика функции
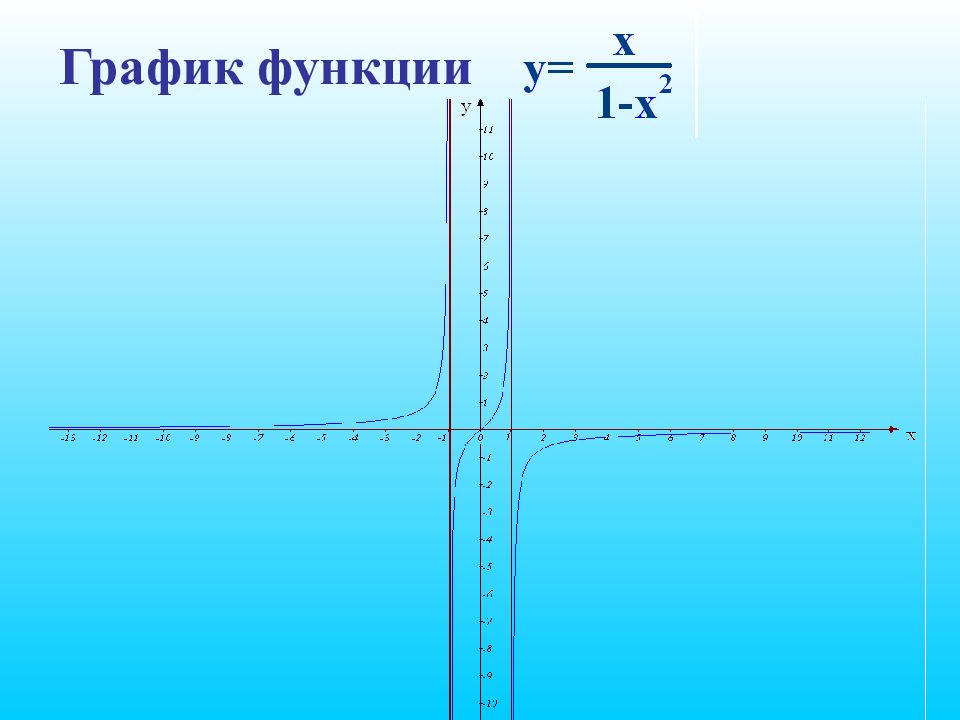
Необходимо исследовать эту функцию и построить ее график Дана функция
1. Найти область определения функции Функция не определена при x = 1 и x = -1. Область ее определения состоит из трех интервалов (- ∞; -1), (-1; 1), (1; +∞), а график из трех ветвей.
Если x = 0, то y = 0. График пересекает ось Oy в точке O (0;0). Если y = 0, то x = 0. График пересекает ось Ox в точке O (0;0).
Функция знакоположительна ( y>0) на интервалах (-∞; -1) и (0; 1). Функция знакоотрицательна ( y<0) на интервалах (-1; 0) и (1; +∞).
Функция является нечетной, т.к. Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при x ≥ 0
Прямые x = 1 и x = -1 являются ее вертикальными асимптотами. Прямая у = 0 является ее горизонтальной асимптотой.
Находим интервалы возрастания и убывания функции. Т.к. , то > 0 в области определения, и функция является возрастающей на каждом интервале области определения.
Находим интервалы возрастания и убывания функции. Т.к., то критическими точками являются точки x 1 = 1 и x 2 = -1 ( не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
Исследуем функцию на выпуклость. Находим :
Вторая производная равна нулю или не существует в точках x 1 = 0, x 2 = -1 и x 3 = 1. Точка О(0; 0) – точка перегиба графика функции. График выпуклый вверх на интервалах (-1; 0) и (1; + ∞); выпуклый вниз на интервалах (-∞; -1) и (0; 1).
