Первый слайд презентации: Экстремум функции двух переменных
Опр. Точка называется точкой максимума функции z=f(x,y), если существует окрестность точки M, такая что для любой точки (x,y) из этой окрестности М X Y Z
Слайд 2: Экстремум функции двух переменных
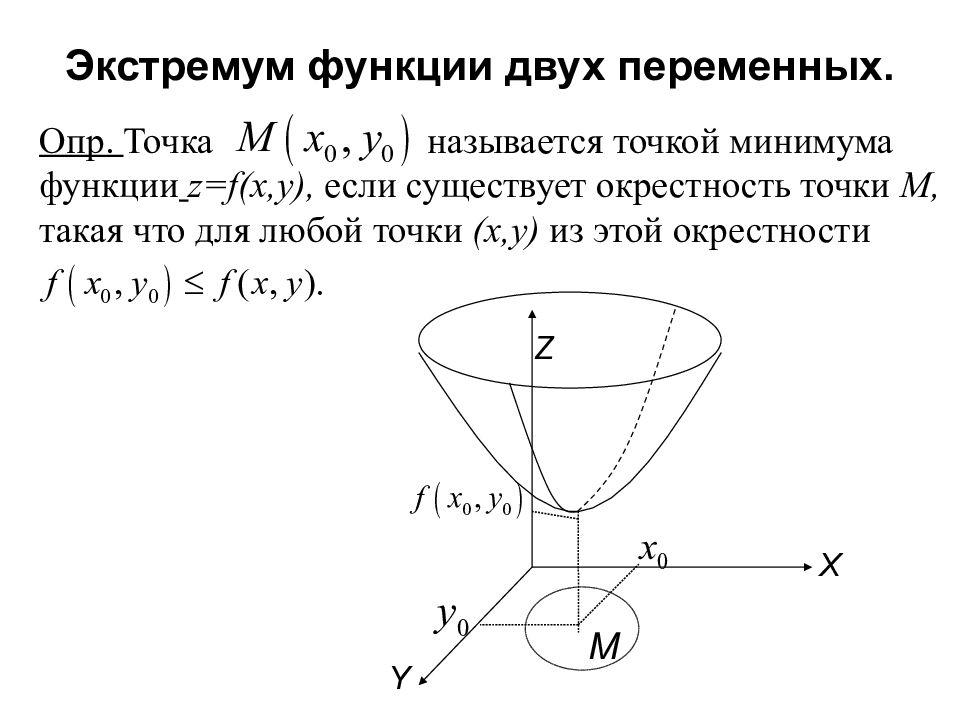
Опр. Точка называется точкой минимума функции z=f(x,y), если существует окрестность точки M, такая что для любой точки (x,y) из этой окрестности М X Y Z
Слайд 3: Экстремум функции двух переменных
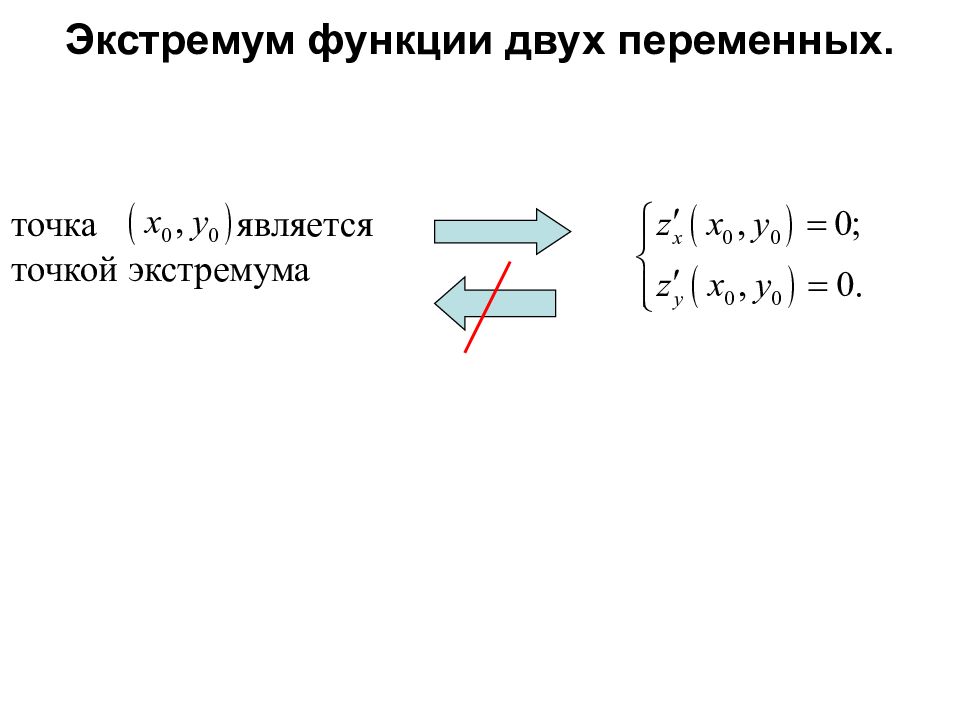
Опр. Точки минимума и максимума называются точками экстремума. Необходимое условие экстремума. Пусть - точка экстремума функции z=f(x,y). Тогда Опр. Точки, в которых выполнено необходимое условие экстремума, называются критическими или стационарны- ми.
Слайд 6: Экстремум функции двух переменных
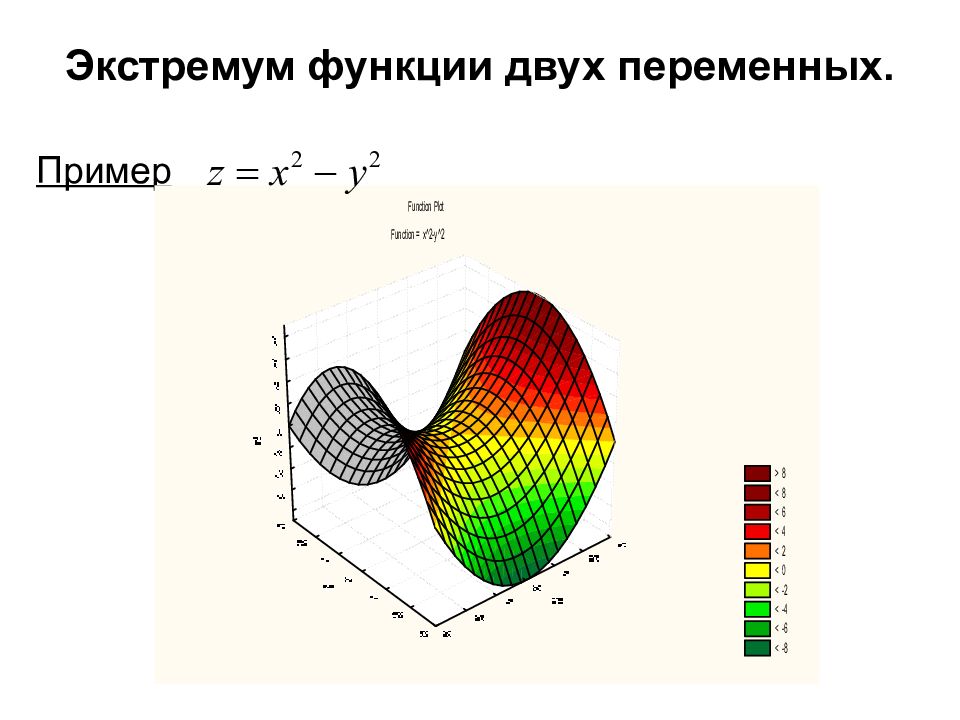
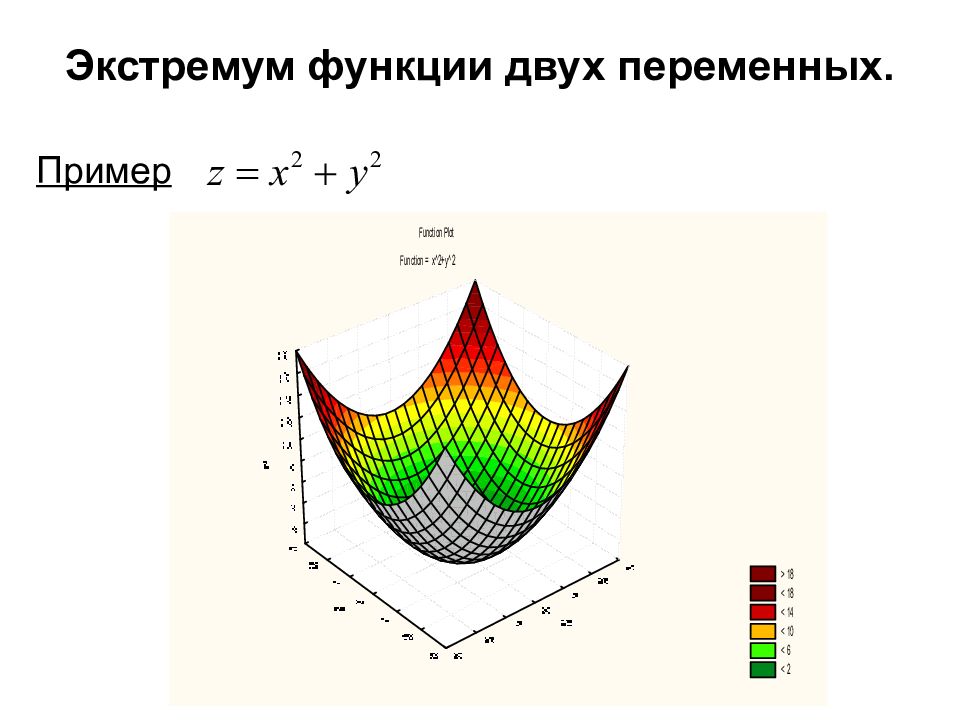
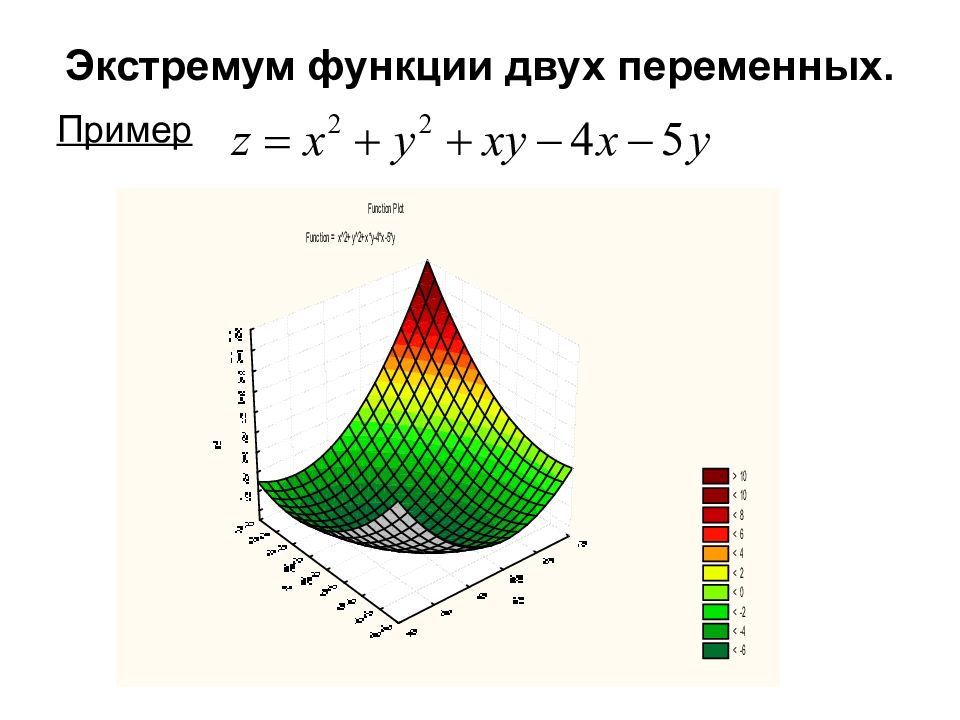
Пример стационарная точка. Является ли она точкой экстремума ?
Слайд 9: Экстремум функции двух переменных
Пример стационарная точка. Является ли она точкой экстремума ?
Слайд 11: Экстремум функции двух переменных
Достаточное условие экстремума. Пусть - крити- ческая точка функции z=f(x,y).
Слайд 12: Экстремум функции двух переменных
Если то - точка максимума Экстремум функции двух переменных. Достаточное условие экстремума. Пусть - крити- ческая точка функции z=f(x,y). Тогда
Слайд 13: Экстремум функции двух переменных
Если то - точка максимума Если то - точка минимума Экстремум функции двух переменных. Достаточное условие экстремума. Пусть - крити- ческая точка функции z=f(x,y). Тогда
Слайд 14: Экстремум функции двух переменных
Если то - точка максимума Если то - точка минимума Если то не является точкой экстремума Экстремум функции двух переменных. Достаточное условие экстремума. Пусть - крити- ческая точка функции z=f(x,y). Тогда