Слайд 2: Домашнее задание
§ 2.1 – 2.2, стр. 46 - 62, в опрос 1 6, стр. 55 Вопрос 6, стр. 62 РТ. № 99, 111, 113
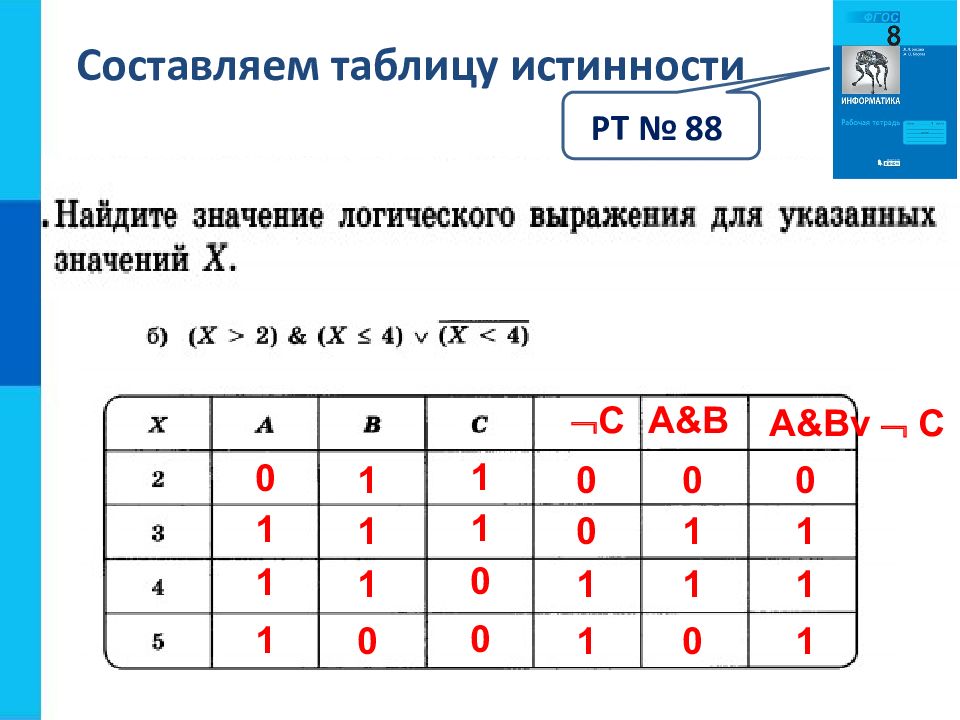
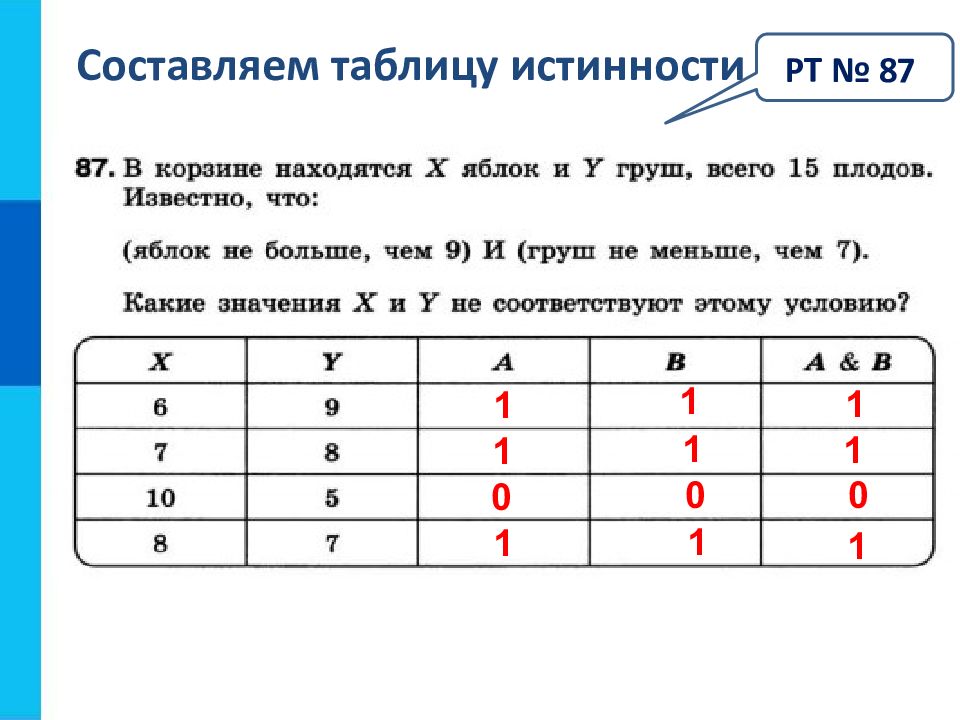
Слайд 7: Составляем таблицу истинности
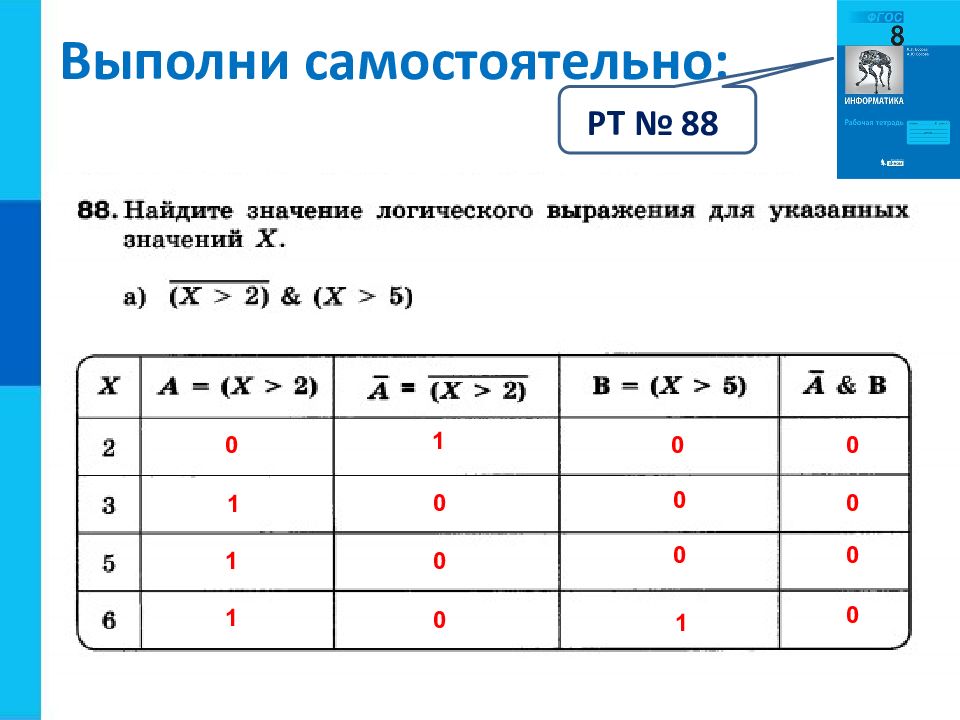
0 РТ № 88 1 1 A&B C A&Bv C 0 0 0 1 1 1 0 1 1 1 1 0 1 1 1 1 0 0 1 0 1
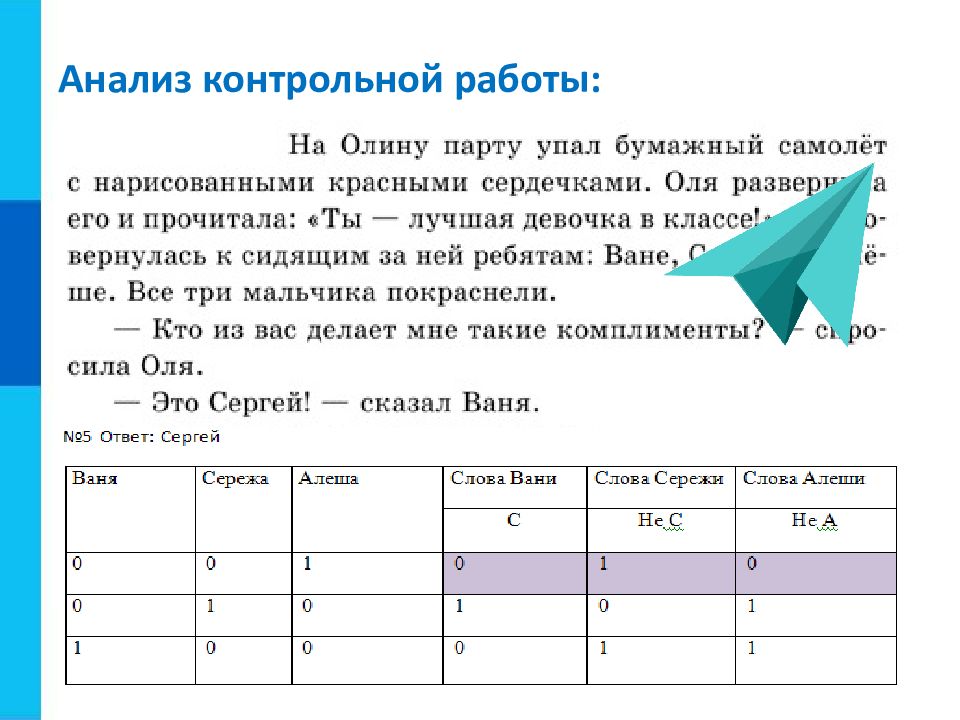
Слайд 12
Алгоритмы и исполнители. Способы записи алгоритмов Практическая работа № 4. алгебра логики высказывание логическая операция конъюнкция дизъюнкция отрицание логическое выражение таблица истинности законы логики Тематический модуль 3: Основы алгоритмизации
Слайд 13: Задачи урока:
Познакомиться: с видами исполнителей. Узнать: об алгоритмах и их свойствах. Цели урока: Научиться: составлять алгоритмы и записывать их разными способами.
Слайд 16: Алгоритмы и исполнители
Алгоритм – это точное и понятное предписание исполнителю выполнить последовательность команд приводящую к результату за конечное количество шагов Алгоритмы и исполнители Дискретность Свойства алгоритма Понятность Определённость Результативность Массовость а лгоритм разделён на отдельные шаги (действия) алгоритм состоит только из команд, входящих в СКИ в алгоритме нет команд, смысл которых может быть истолкован неоднозначно алгоритм обеспечивает получение результата после конечного числа шагов алгоритм обеспечивает решения целого класса однотипных задач
Слайд 17: Работа с учебником
§ 2.2 стр. 57 - 61 Ответьте не вопрос: какие существуют способы записи алгоритмов
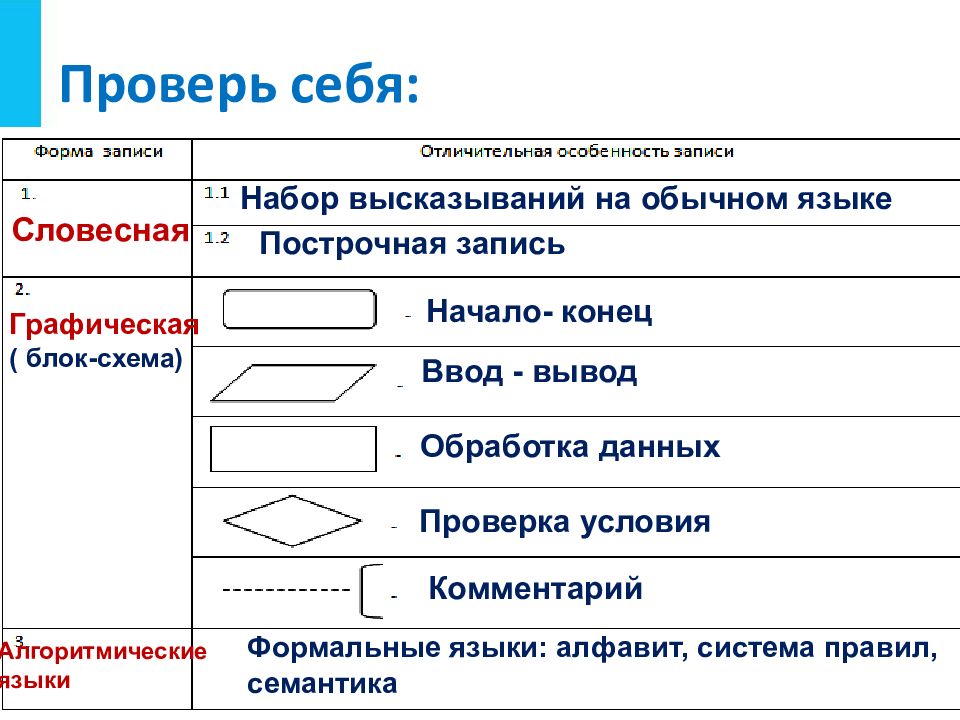
Слайд 18: Проверь себя:
Словесная Набор высказываний на обычном языке Построчная запись Графическая ( блок-схема) Ввод - вывод Обработка данных Начало- конец Проверка условия Комментарий Алгоритмические языки Формальные языки: алфавит, система правил, семантика
Слайд 24: Работа за компьютером
! Работа за компьютером Практическая работа № 4. Непосредственное и программное управление исполнителем РТ № 98 а
Слайд 25
Вам было легко или были трудности? Что у вас получилось лучше всего и без ошибок? Какое задание было самым интересным и почему? Как бы вы оценили свою работу ? Подведение итогов урока:
Слайд 26: Устное повторение:
Что изучает наука логика? Что такое высказывание? Какие выражения являются высказываниями, а какие нет? С помощью каких языков можно построить высказывание? Какие логические операции используются для составления сложных высказываний на языке алгебры логики? Как они обозначаются? Какие возможные значения могут иметь логические выражения? Какие логические операции вы знаете? Как построить таблицу истинности сложного высказывания? Устное повторение:
Слайд 27: Устное повторение
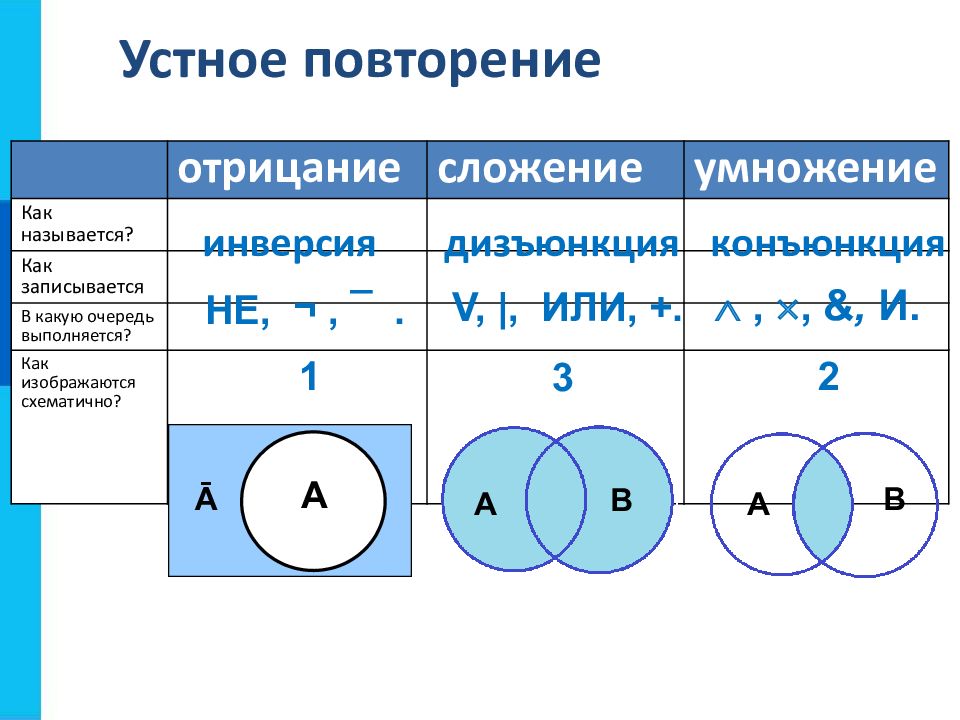
отрицание сложение умножение Как называется? Как записывается В какую очередь выполняется? Как изображаются схематично? инверсия дизъюнкция конъюнкция , , &, И. V, |, ИЛИ, +. НЕ, ¬, ¯. 1 3 2 A Ā A B A B
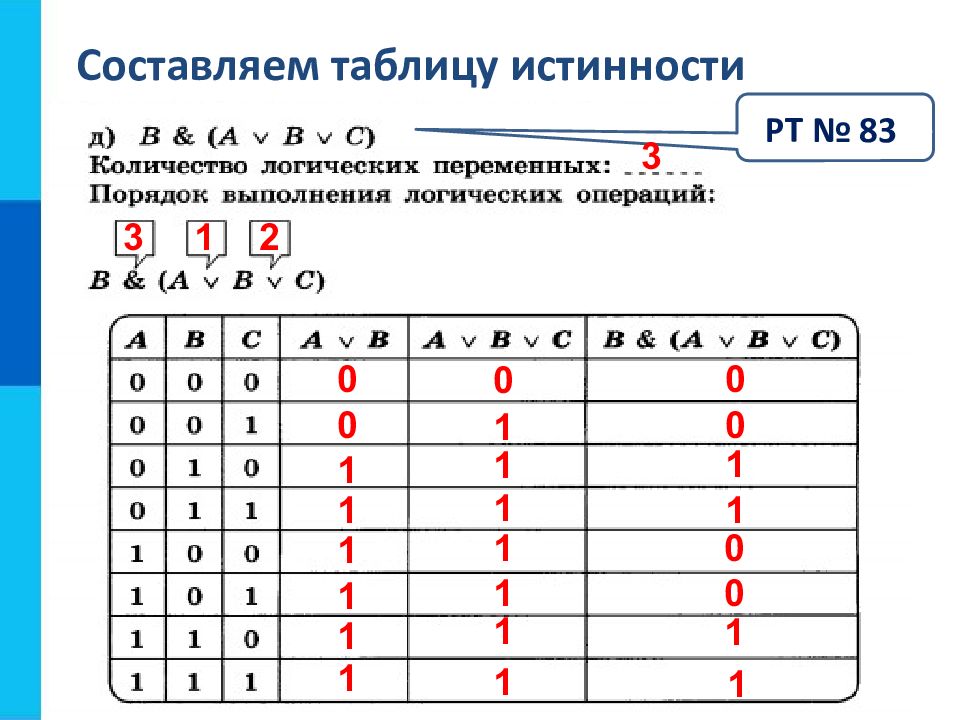
Слайд 28: Составляем таблицу истинности
РТ № 83 3 1 2 3 0 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 1 0 0 1 1
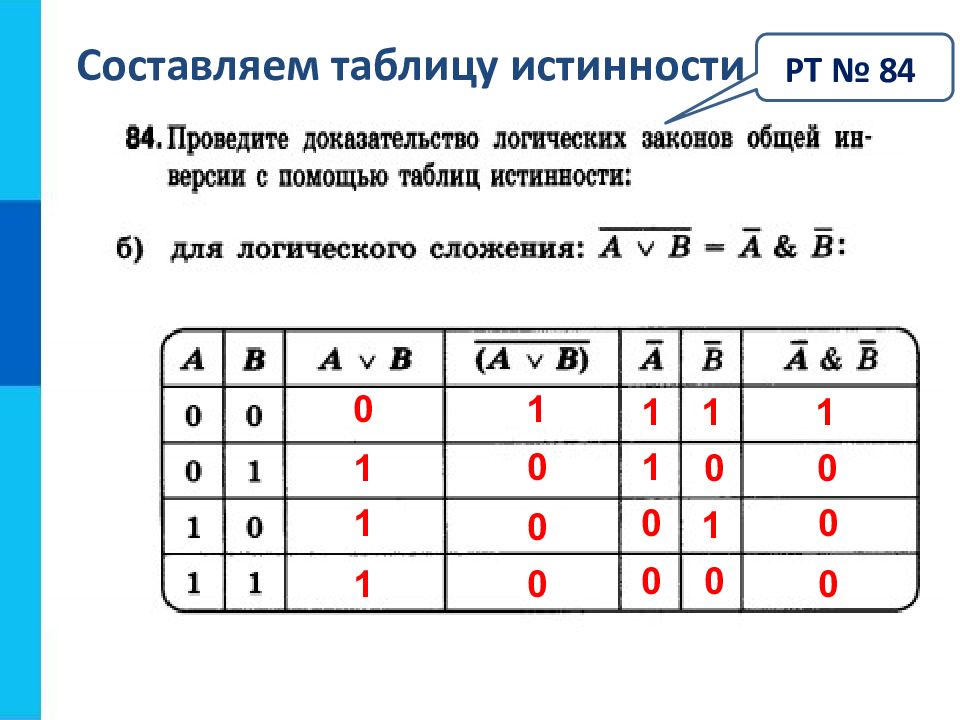
Слайд 29: Составляем таблицу истинности
РТ № 84 0 1 1 1 1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 0
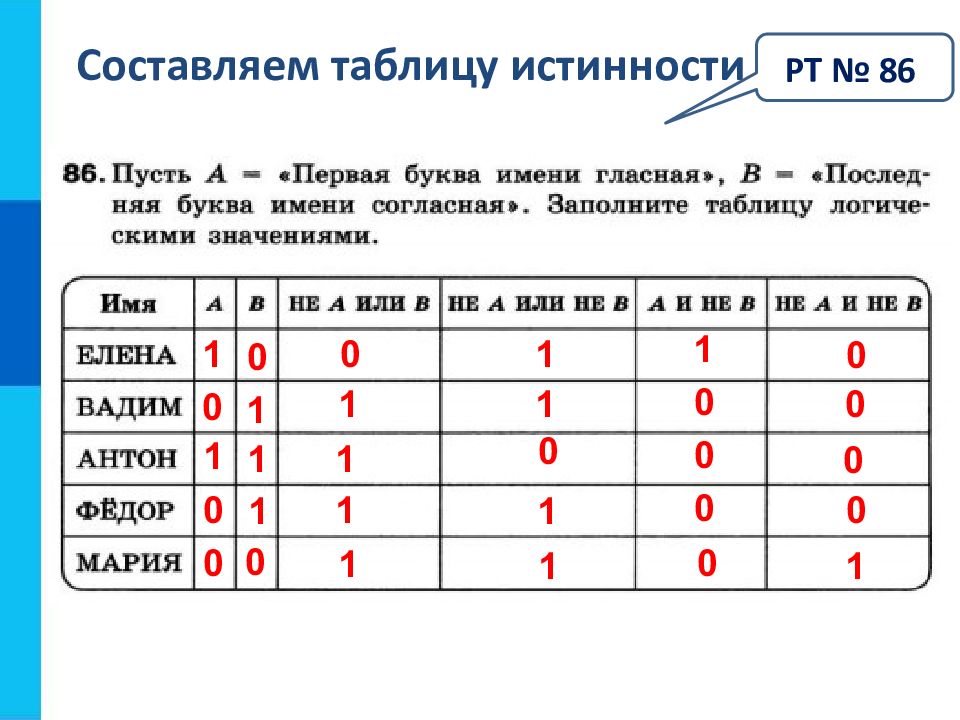
Слайд 30: Составляем таблицу истинности
РТ № 86 1 0 0 1 1 1 0 1 0 0 0 1 1 1 1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 1
Слайд 32: Расскажи, как бы ты упростил следующее алгебраическое выражение?
( a * b ) + ( a * c ) a * ( b + c) Какой закон алгебры ты применил ? Каковы его свойства? Распределительный закон Расскажи, как бы ты упростил следующее логическое выражение? ( a & b ) V (a & с ) a & ( b V с )
Слайд 33
Что ты можешь сказать о свойствах алгебраических и логических выражений? Алгебраическое выражение Логическое выражение a*b +a*c = a*(b + c) ( a & b) V ( a & с ) = a & ( b V с )
Слайд 34: Задачи урока:
Научиться : доказывать справедливость законов логики. Узнать: о свойствах логических операций. составлять таблицы истинности для решения логических задач. как решаются логические задачи?
Слайд 39
Логические элементы алгебра логики высказывание логическая операция конъюнкция дизъюнкция отрицание логическое выражение таблица истинности законы логики Тематический модуль 2: Математические основы информатики
Слайд 40: Задачи урока:
Познакомиться: с принципами работы логических элементов. Узнать: что такое логические элементы и где они применяются? Цели:
Слайд 42
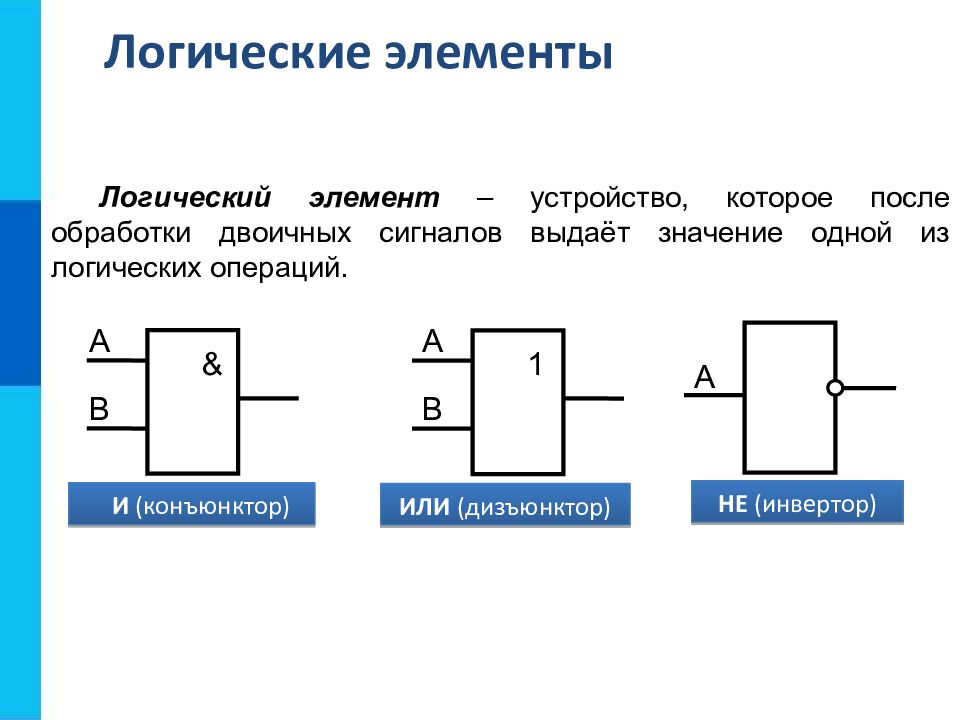
Логический элемент – устройство, которое после обработки двоичных сигналов выдаёт значение одной из логических операций. & А В И ( конъюнктор ) 1 А В ИЛИ ( дизъюнктор ) НЕ (инвертор) А Логические элементы