Первый слайд презентации: Тема №9 Матрицы
Цель темы: матрицы и действия над матрицами: определители.
Слайд 2: Понятие о матрице
Таблица чисел вида, состоящая из m столбцов и n строк, называется матрицей размера m на n. Диагональ матрицы
Слайд 3: Определения
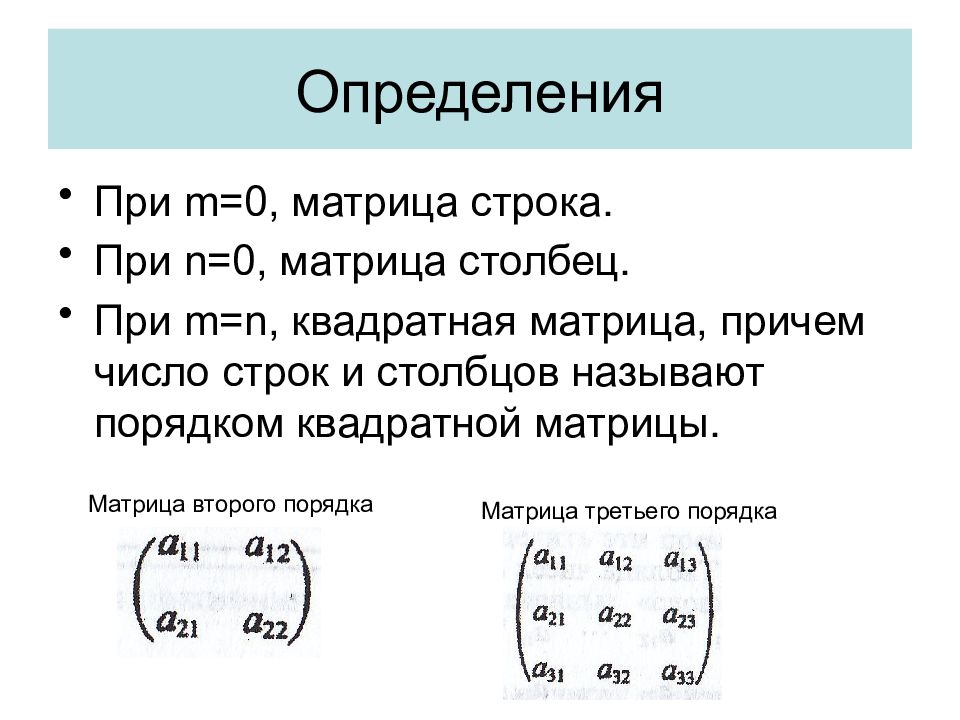
При m=0, матрица строка. При n= 0, матрица столбец. При m=n, квадратная матрица, причем число строк и столбцов называют порядком квадратной матрицы. Матрица второго порядка Матрица третьего порядка
Слайд 4: Равенство матриц
Две матрицы А и В называют равными А=В, если они одинакового размера (то есть имеют одинаковое число строк и столбцов) и их соответствующие элементы равны.
Слайд 5: Сложение матриц
Матрицы одинакового размера можно сложить. Суммой двух матриц А и В будет матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. ПРИМЕР
Слайд 6: Сложение матриц
Сложение матриц подчиняется переместительному и сочетательному закону. Матрица все элементы которой равны нулю называется нуль матрицей
Слайд 7: Вычитание матриц
Разностью двух матриц А и В одинакового размера называется матрица С, такая что А В С
Слайд 8: Умножение матрицы на число
Произведением матрицы А на число L называется матрица, элементы которой равны произведению числа L на соответствующие элементы матрицы А.
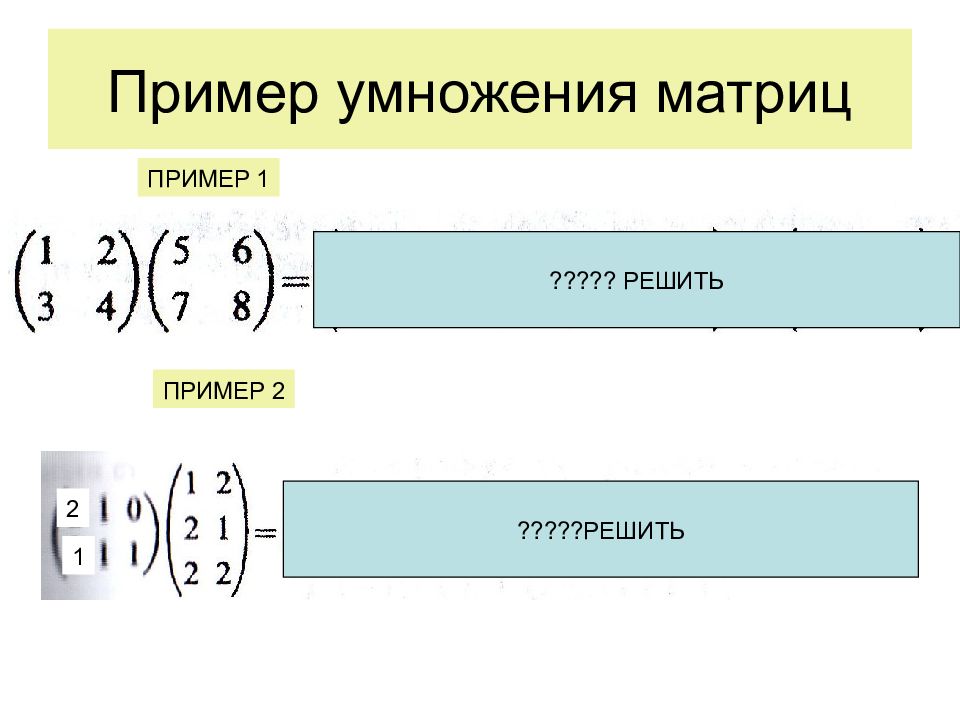
Слайд 9: Умножение матриц
Элемент матрицы произведения, находящийся на пересечении i- строки и k- столбца, представляет собой сумму парных произведений элементов i- строки первой матрицы на элементы k- столбца второй матрицы. Это правило сохраняется при умножении квадратных матриц и прямоугольных, у которых число столбцов матрицы множимого равно числу строк матрицы множителя
Слайд 12: Пример 3
ВЫВОДЫ: В результате перемножения двух матриц получается матрица, содержащая столько строк сколько их имеет матрица множимое, и столько столбцов сколько их имеет матрица множитель.
Слайд 14: ПРИМЕР 3
ВЫВОД Произведение двух матриц не подчиняется переместительному закону Произведение матриц подчиняется сочетательному закону
Слайд 15: Особенность произведения матриц
Известно, что произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может не выполняться. ПРОВЕРИТЬ!!!!
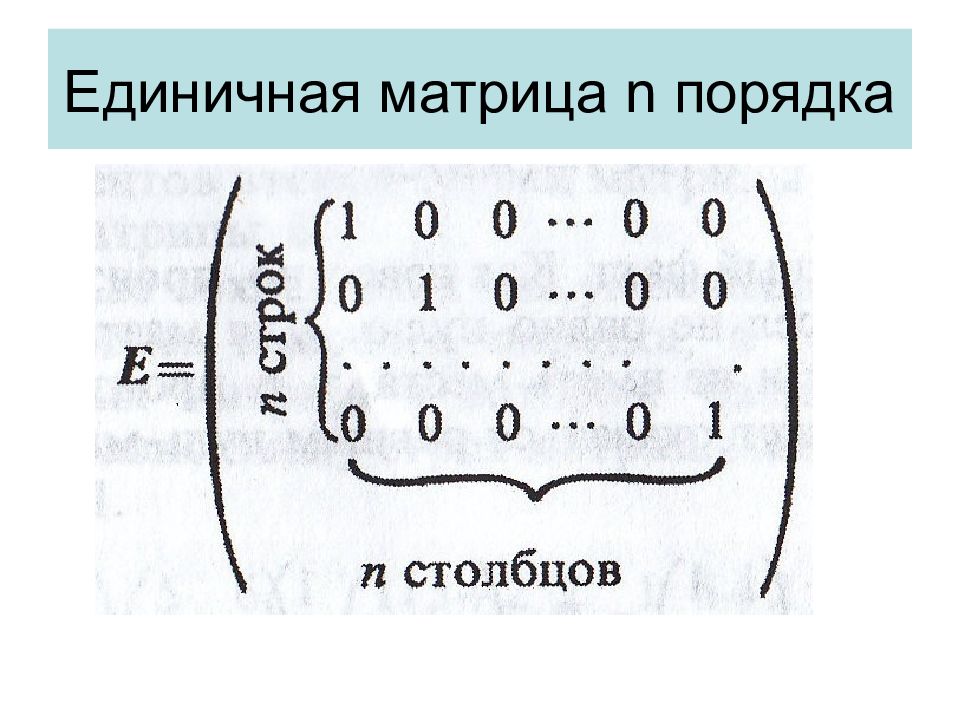
Слайд 17: Свойство единичной матрицы
Матрица вида Е – называется единичной матрицей. При умножении любой квадратной матрицы А второго порядка на единичную матрицу получаем матрицу А. Аналогично ЕА=А
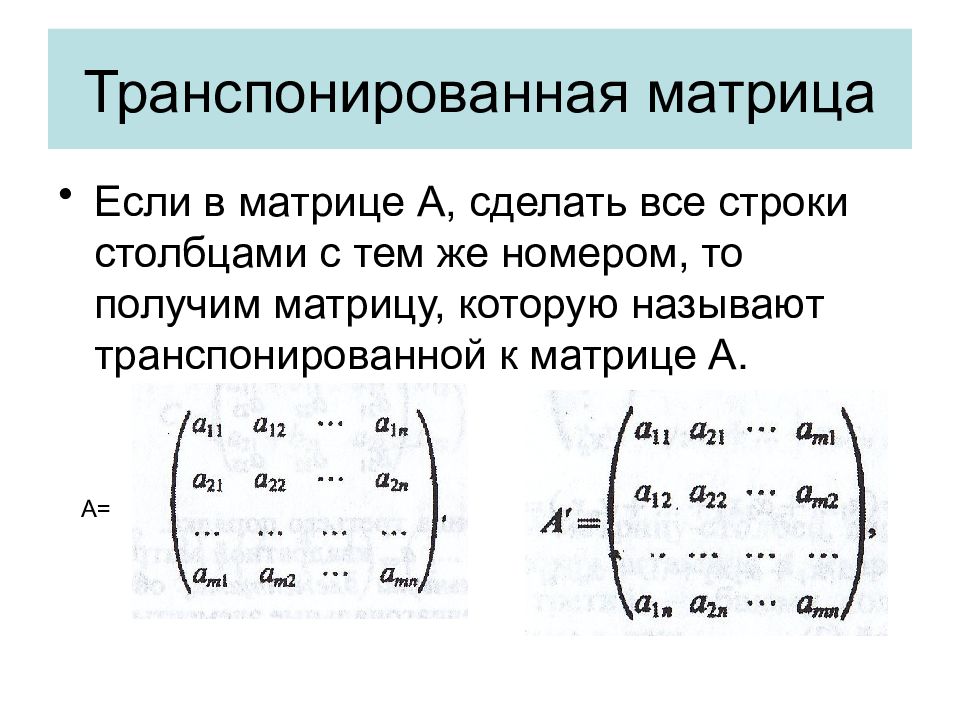
Слайд 19: Транспонированная матрица
Если в матрице А, сделать все строки столбцами с тем же номером, то получим матрицу, которую называют транспонированной к матрице А. А=
Слайд 20: Диагональная матрица
Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые.
Слайд 21: Определитель второго порядка
Определителем второго порядка, соответствующим матрице А, называется число, равное а11а22-а12а21. ЭЛЕМЕНТЫ ОПРЕДЕЛИТЕЛЯ Главная диагональ Побочная диагональ
Слайд 23: Свойства определителя
Величина определителя не меняется, если его строки заменить соответствующими столбцами Меняется знак, если поменять местами его строки или столбцы. Увеличивается в k раз, если элементы какого-либо столбца или строки увеличить в k раз, то есть общий множитель имеющийся в строке или столбце, можно выносить за знак определителя. Равна нулю, если элементы какого-либо его столбца или строки равны нулю. Равна нулю, если элементы двух строк или столбцов соответственно равны.
Слайд 24: Определители третьего порядка
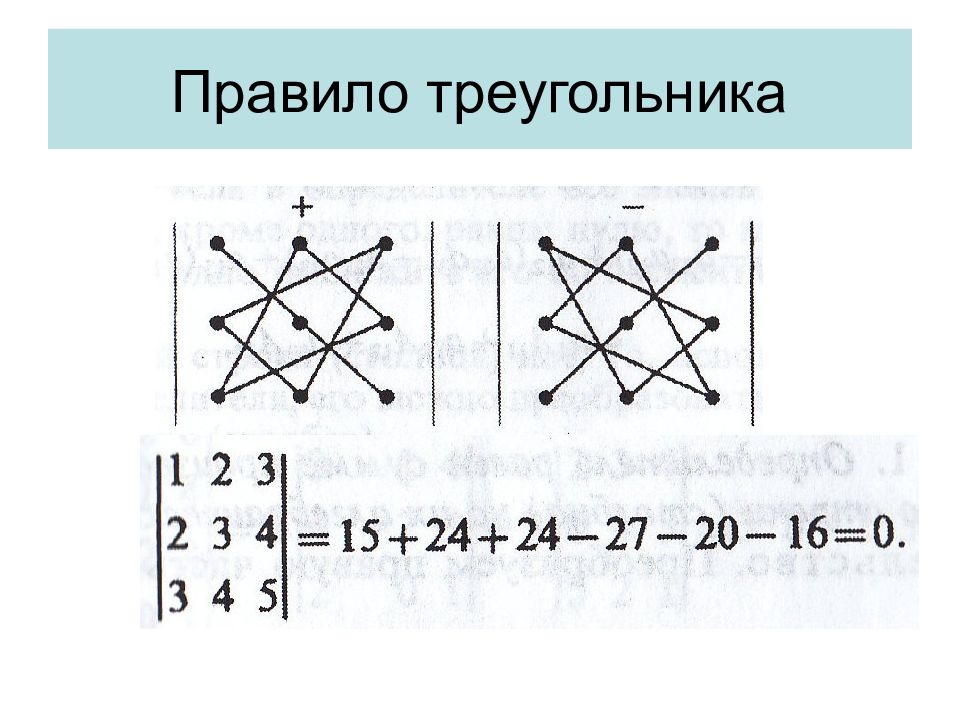
Определителем третьего порядка, соответствующим матрице А, называется число равное а11а22а33+а12а23а31+а13а21а32-а13а22а31-а11а23а32-а12а21а23
Слайд 26: Свойства определителей третьего порядка
Все свойства определителя второго порядка остаются справедливыми для определителей третьего порядка Единичная матрица третьего порядка
Слайд 27: Минор элемента определителя
Минором какого-либо элемента определителя называется определитель, полученный из данного вычеркиванием той строки и столбца, которым принадлежит данный элемент. Например минором а12 является = M 12
Слайд 28: Алгебраическое дополнение элемента определителя
Называется его минор взятый со знаком минус Порядок в строке Порядок в столбце Если сумма I и k четно, то А имеет знак минус. Если сумма I и k нечетно, то А имеет знак плюс.
Слайд 29: Теорема
Определитель равен сумме произведений элементов какой либо строки или столбца на их алгебраические дополнения. ДОКАЗАТЕЛЬСТВО : Данная формула называется разложением определителя по элементам первой строки дополнение
Слайд 30: ЗАДАЧА
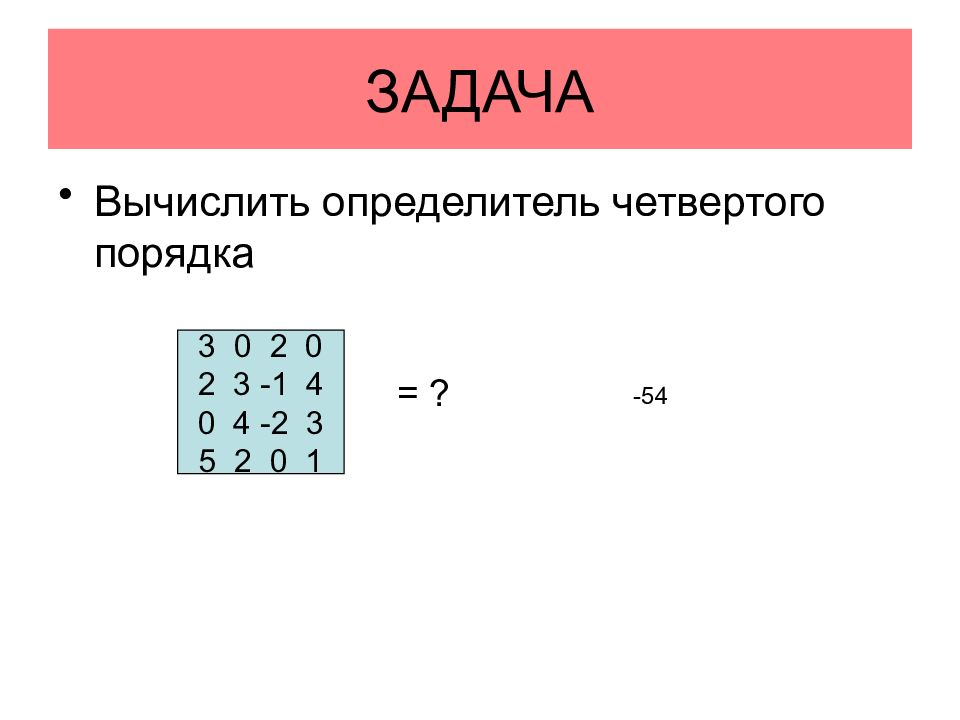
Вычислить определитель четвертого порядка 3 0 2 0 2 3 -1 4 0 4 -2 3 5 2 0 1 = ? -54
Слайд 31: Теорема
Если А и В – квадратные матрицы одного порядка с определителями ! А! и !В!, то определитель матрицы С = АВ равен произведению определителей умножаемых матриц.
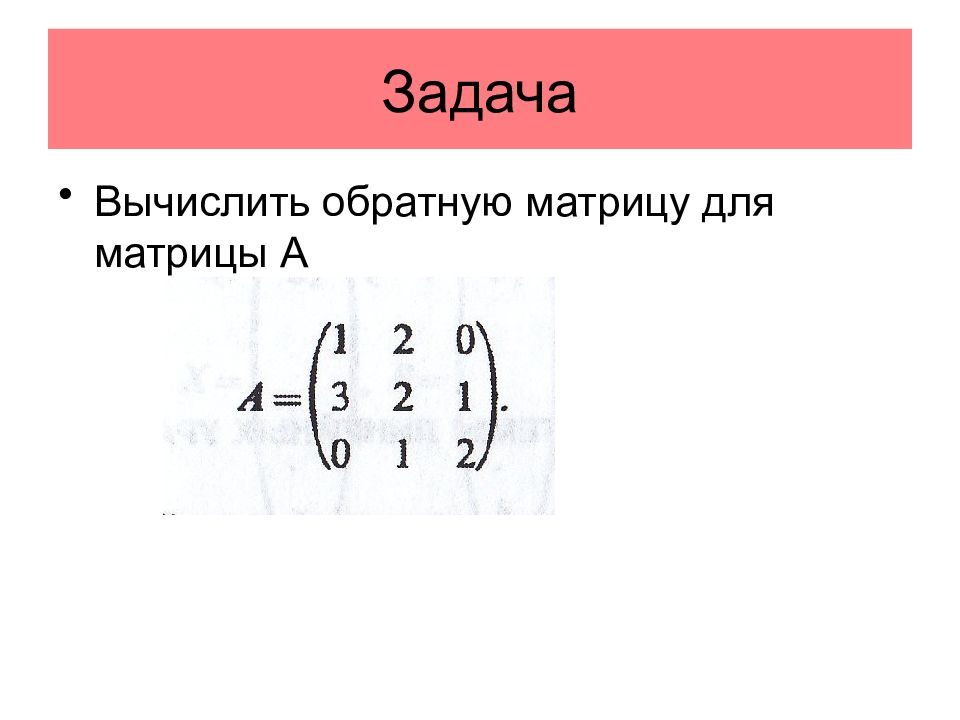
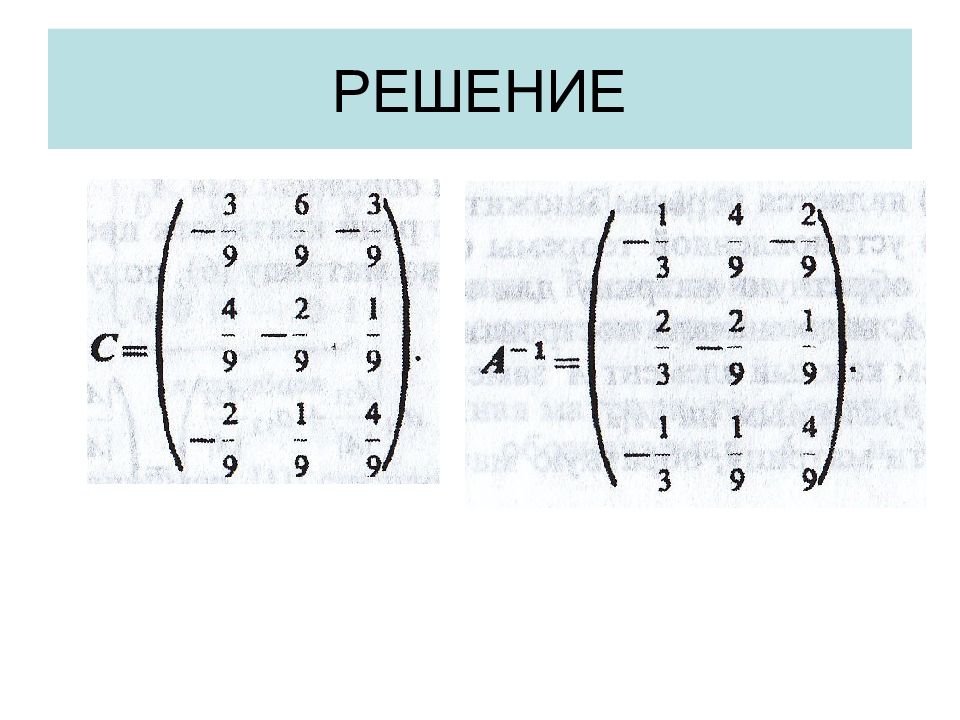
Слайд 32: Обратная матрица
Только для квадратных матриц, имеющих не нулевой определитель. Если А – квадратная матрица, то обратной для нее матрицей называется матрица, удовлетворяющая условию Дополнения элемента а11 Чтобы построить обратную матрицу, необходимо Сначала каждый элемент заменить его алгебраическим дополнением, деленным на определитель, а затем. построить транспонированную матрицу.