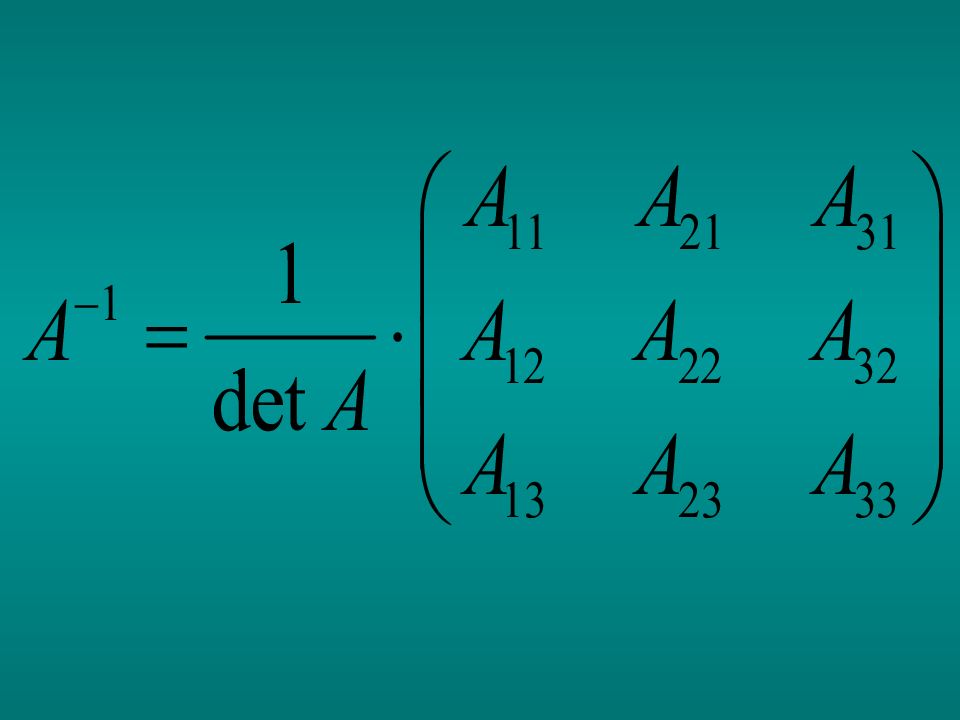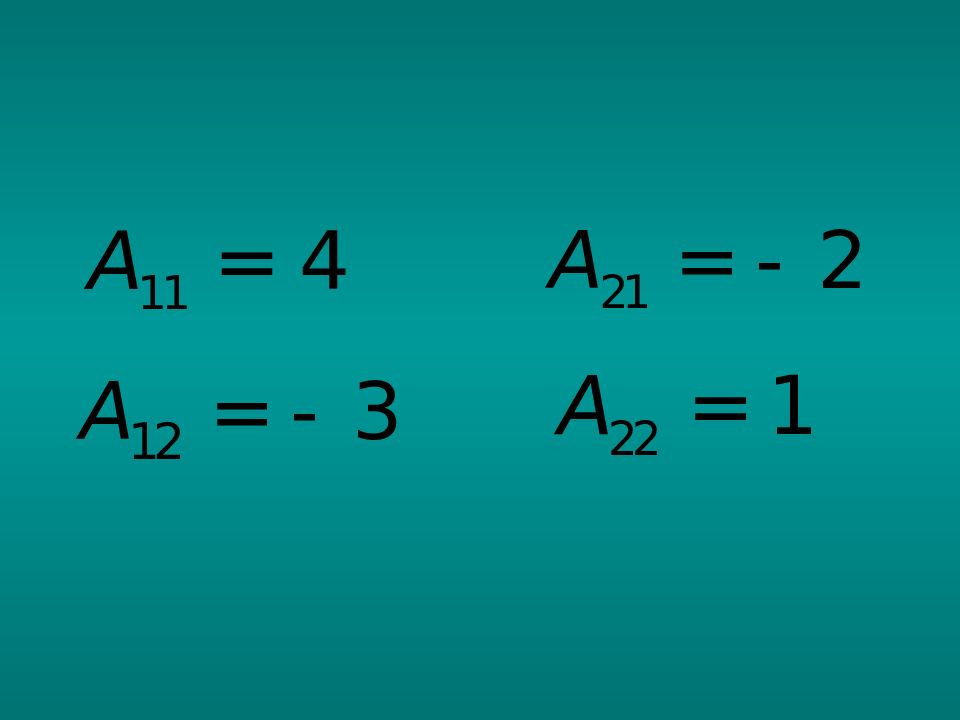Обратная матрица обозначается символом Примечание. Операция деления для матриц не определена. Вместо этого предусмотрена операция обращения (нахождения обратной) матрицы.
1. Находим определитель матрицы А. Он должен быть отличен от нуля. 2. Находим алгебраические дополнения для каждого элемента матрицы А. 3. Составляем союзную матрицу и транспонируем ее. 4. Подставляем результаты п.1 и п.4 в формулу обратной матрицы.
Р е ш е н и е. Действуем по алгоритму: 1. Находим определитель матрицы: Определитель отличен от нуля, следовательно, обратная матрица существует.
2. Находим алгебраические дополнения:
3. Составляем союзную матрицу:
4. Записываем обратную матрицу по формуле
Воспользуемся определением обратной матрицы и найдем произведение
перестановка строк (столбцов) местами; исключение из матрицы строк (столбцов), состоящих из нулей; умножение всех элементов какой-либо строки (столбца) матрицы на любое число, отличное от нуля; прибавление к одной строке (столбцу) другой, предварительно умноженной на любое число, отличное от нуля.
Определение. Э к в и в а л е н т н ы м и называются матрицы, полученные одна из другой путем элементарных преобразований. Важным понятием для матриц является понятие РАНГА. Существует несколько определений этого понятия. Мы остановимся на одном из них, основанном на элементарных преобразованиях. Определение. Р а н г о м м а т р и ц ы называется число ненулевых строк в матрице, после приведения ее к ступенчатому виду (путем элементарных преобразований). Обозначение. Ранг матрицы будем обозначать или. Теорема. Ранг матрицы не меняется при элементарных преобразованиях.
