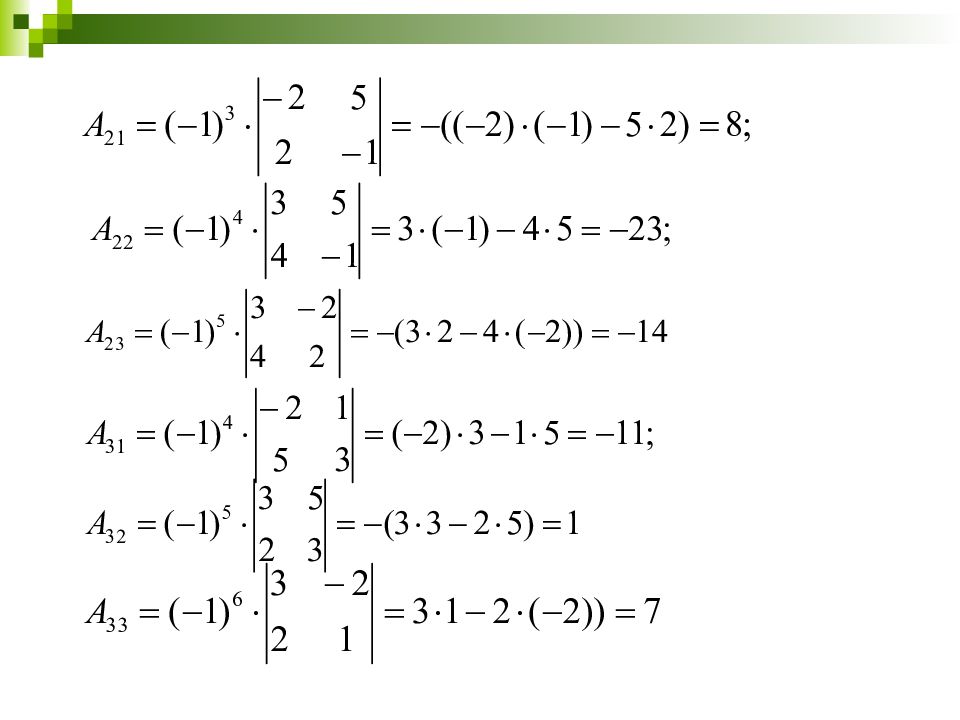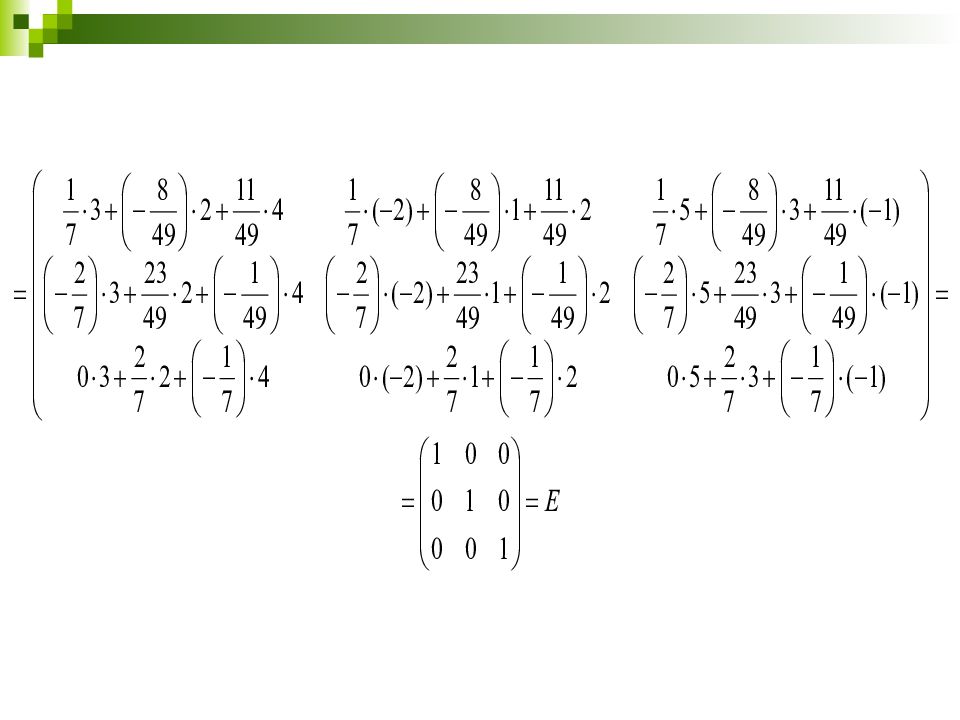Матрица A -1 называется обратной к матрице А, если А A -1 = A -1 А=Е где Е – единичная матрица
Алгоритм нахождения обратной матрицы 1 Определяем, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
2 Находим определитель матрицы. Если он равен нулю, то обратной матрицы не существует.
3 Заменяем каждый элемент матрицы его алгебраическим дополнением.
4 Полученную матрицу транспонируем.
5 Каждый элемент полученной матрицы делим на определитель исходной матрицы. Получаем матрицу, обратную к данной.
6 Делаем проверку. Для этого перемножаем полученную и исходную матрицы. Должна получиться единичная матрица.
Пример. Найти матрицу, обратную к матрице
Применяем алгоритм нахождения обратной матрицы. Решение: Находим определитель: Матрица квадратная, следовательно обратная матрица для нее существует. 1 2
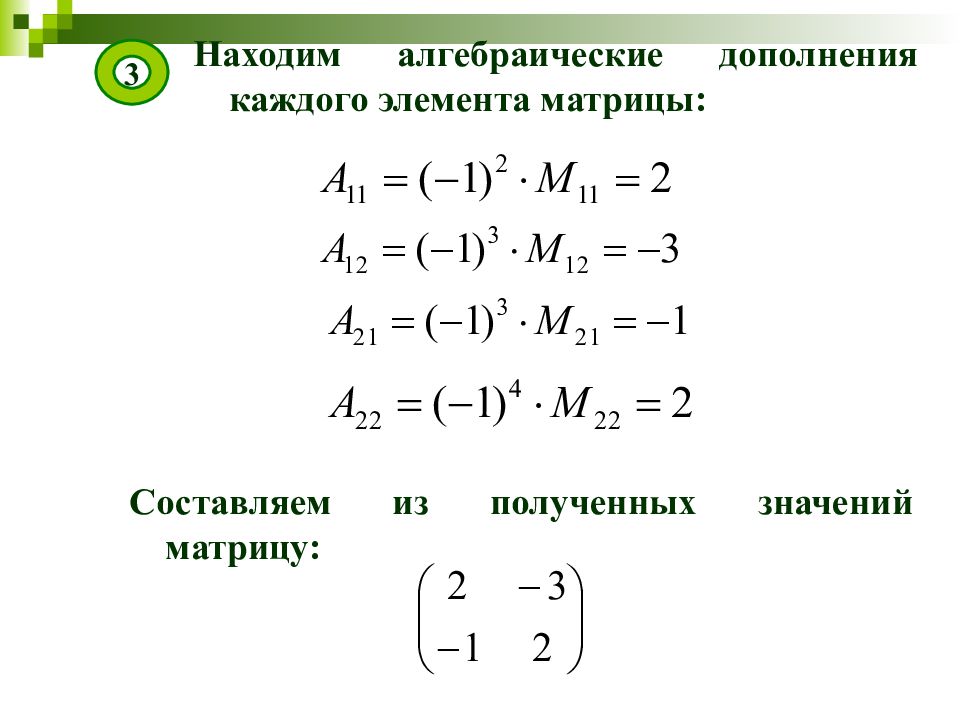
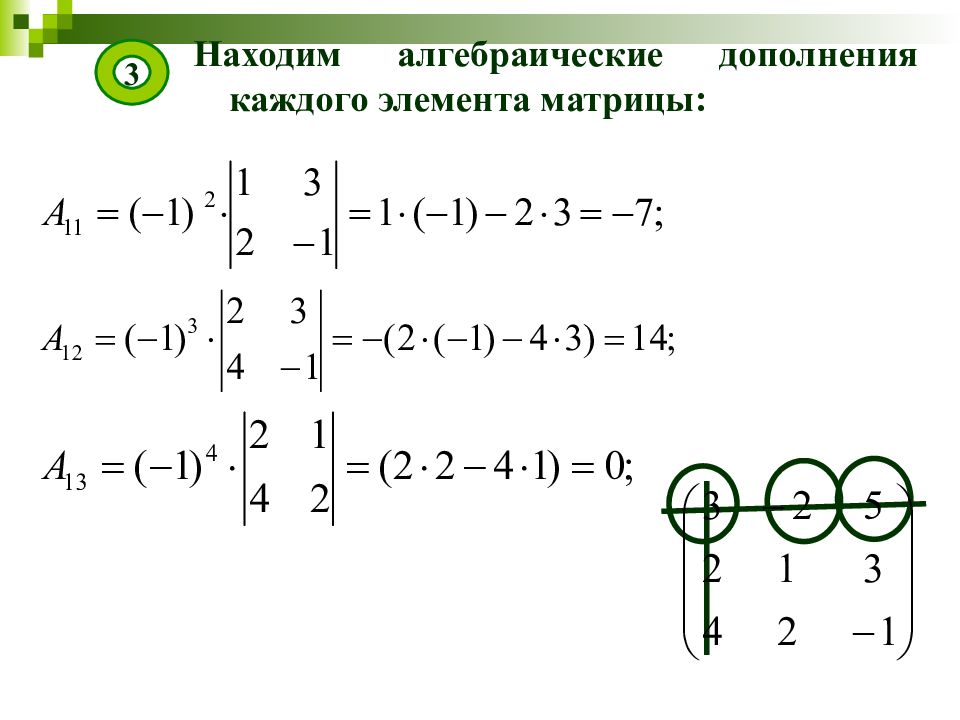
Находим алгебраические дополнения каждого элемента матрицы: 3 Составляем из полученных значений матрицу:
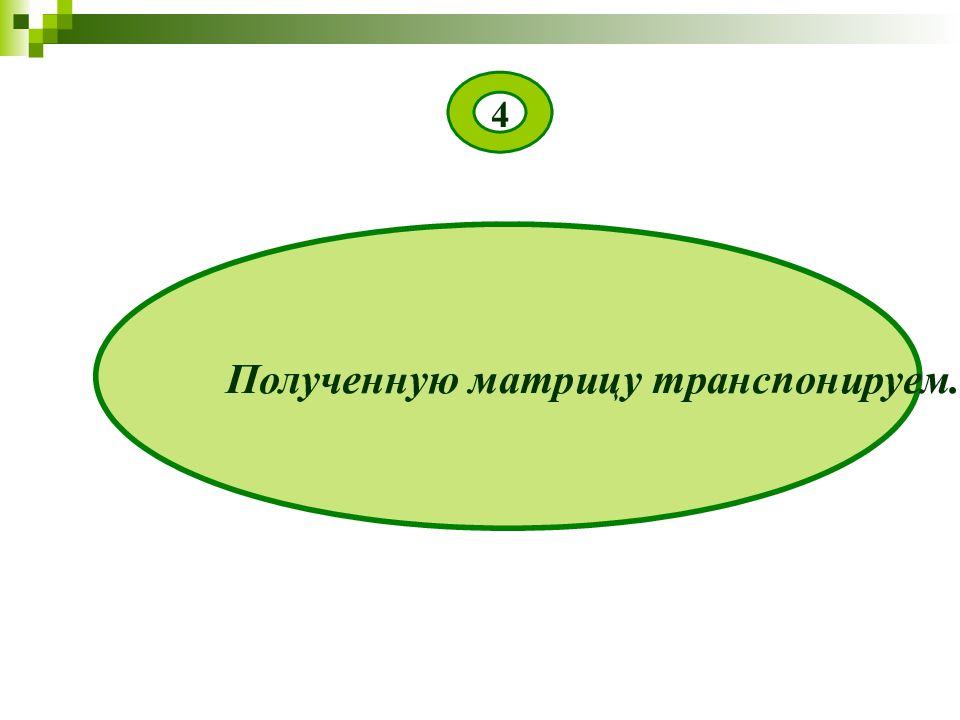
Транспонируем ее: Каждый элемент матрицы делим на определитель Δ =1 и получаем обратную матрицу: 4 5
Проверяем: 6
Пример. Найти матрицу, обратную к данной и сделать проверку
Применяем алгоритм нахождения обратной матрицы. Решение: Находим определитель: Матрица квадратная, следовательно обратная матрица для нее существует. 1 2
Находим алгебраические дополнения каждого элемента матрицы: 3
Составляем из полученных значений матрицу: 4 Транспонируем ее:
Каждый элемент матрицы делим на определитель Δ =-49 и получаем обратную матрицу: 5
Проверяем: 6
Перестановка местами двух параллельных рядов матрицы; Умножение всех элементов ряда матрицы на число, отличное от нуля; Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
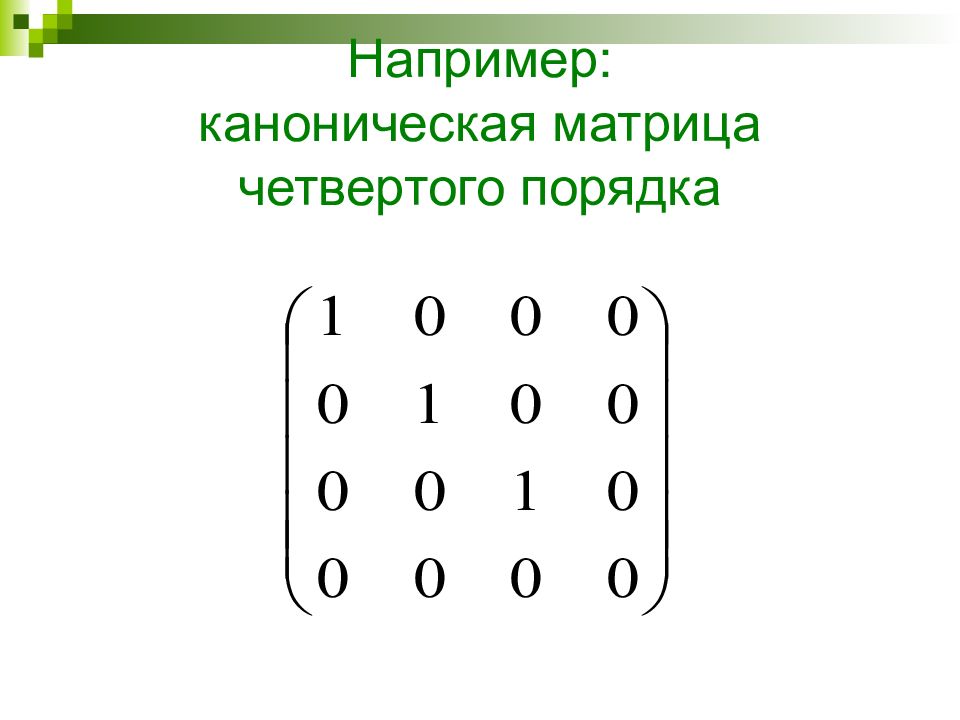
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается: А ~ В. При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале стоят подряд несколько единиц, а все остальные элементы матрицы равны нулю. Такую матрицу называют канонической.
Привести матрицу к каноническому виду: ~ Поменяем местами первый и третий столбцы ~ ~ Прибавим ко второй строке первую и результат запишем на место второй строки
~ ~ Умножим первую строку на -5 и прибавим к третьей строке, результат запишем на место третьей строки ~ -3 -2 -2 ~ ~ :5 :2 :3
~ ~ 3 -1 -1 ~ ~
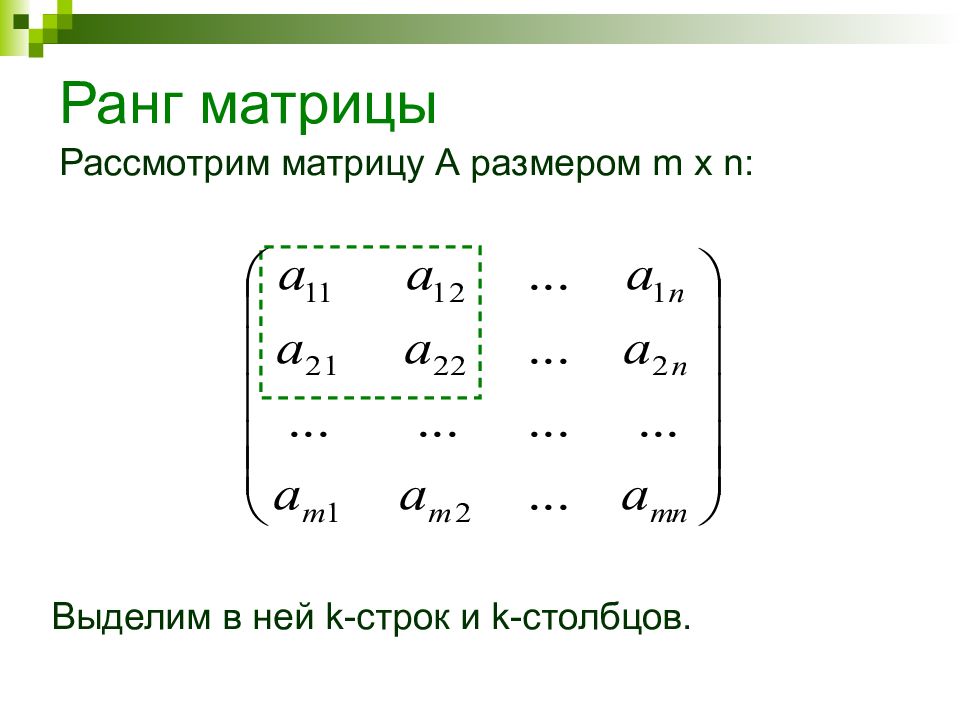
Рассмотрим матрицу А размером m x n : Выделим в ней k- строк и k- столбцов.
Из элементов, состоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы.
Количество подобных миноров определяется по формуле где - число сочетаний из n элементов по k :
Определим число миноров 3-его порядка для матрицы размером 4 х 7: k=3; m=4; n=7
наибольший из порядков миноров данной матрицы, отличных от нуля. Обозначается r, r(A) или rang(A). Минор, порядок которого определяет ранг матрицы, называется базисным.
Пример: Определить ранг матрицы:
Решение: Все миноры третьего порядка равны нулю. Есть минор второго порядка, отличный от нуля: Значит, r(A)=2. Базисный минор стоит на пересечении второй и третьей строки с первым и третьим столбцами.
При транспонировании ранг матрицы не меняется. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Ранг канонической матрицы равен числу единиц на главной диагонали. Это один из способов определения ранга матрицы.
Определить ранг матрицы:
Приведем матрицу к каноническому виду: ~ ~ 2 ~ ~ - ~
… самостоятельно! В результате получим матрицу канонического вида: Таким образом, ранг матрицы равен 3.
n – число столбцов матрицы А или строк матрицы В
В матрице А обозначим ее строки следующим образом: Две строки матрицы называются равными, если равны их соответствующие элементы: если
Строка е называется линейной комбинацией строк e 1, e 2, …, e s матрицы, если она равна сумме произведений этих строк на произвольные действительные числа: e= λ 1 e 1 + λ 2 e 2 +…+ λ s e s где λ i - любые числа.
Строки матрицы e 1, e 2, …, e т называются линейно зависимыми, если существуют такие числа λ 1, λ 2,… λ т,не равные нулю одновременно, что линейная комбинация строк матрицы равна нулевой строке: λ 1 e 1 + λ 2 e 2 +…+ λ т e т = 0, где 0 =(0 0 … 0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных. Пусть λ т 0, тогда e т = ( - λ 1 / λ т ) e 1 + (- λ 2 / λ т ) e 2 +…+(- λ т -1 / λ т )e m-1
Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы). Эта теорема играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
