Первый слайд презентации: Параллельность плоскостей
Слайд 3: Определение
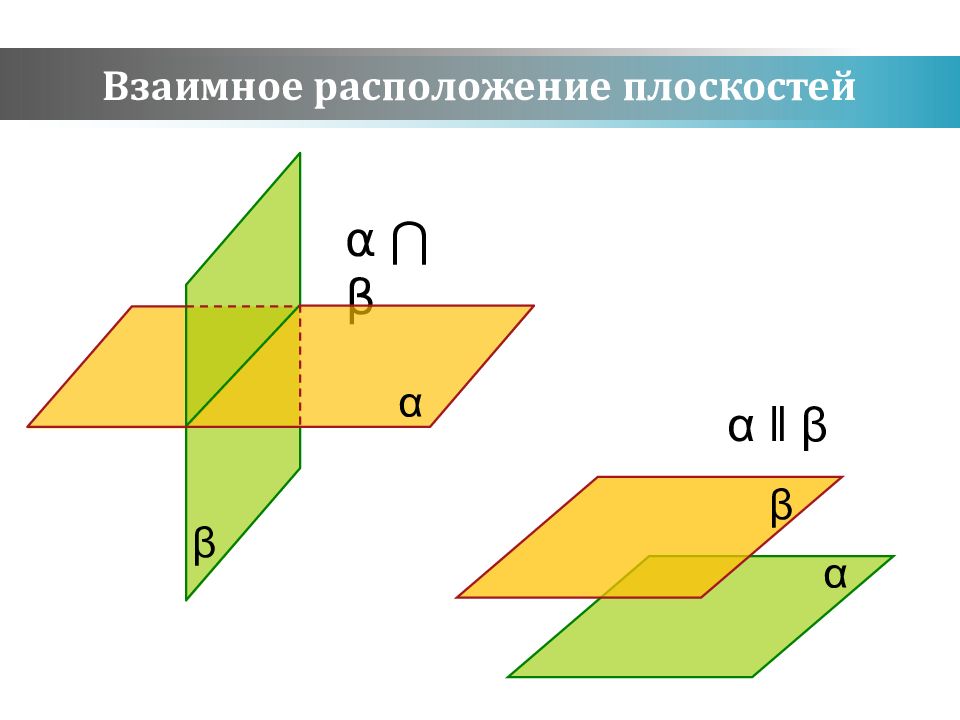
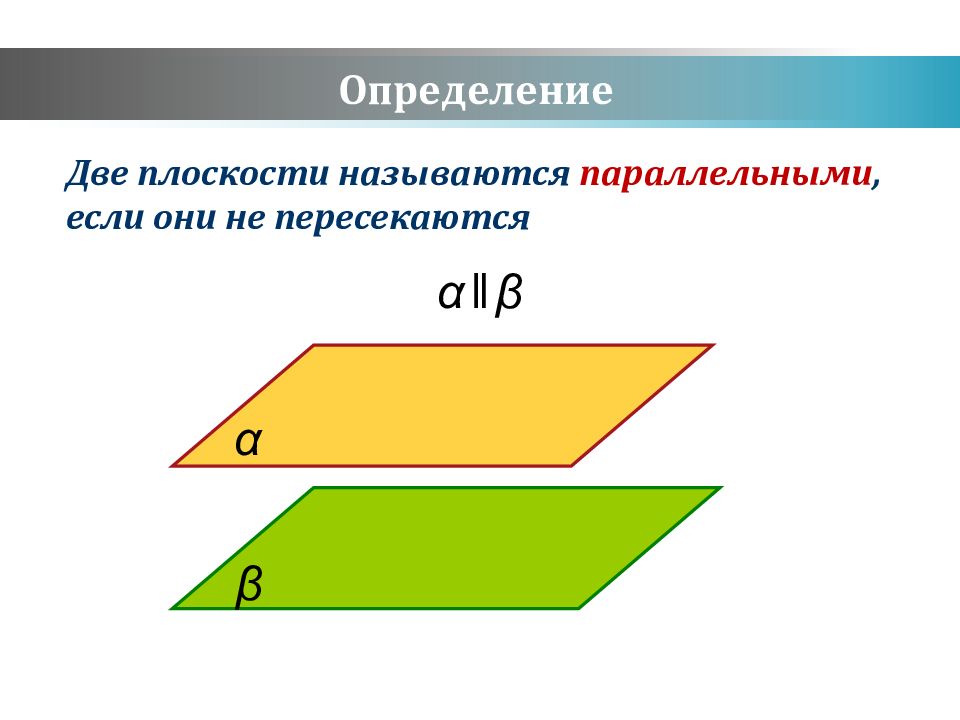
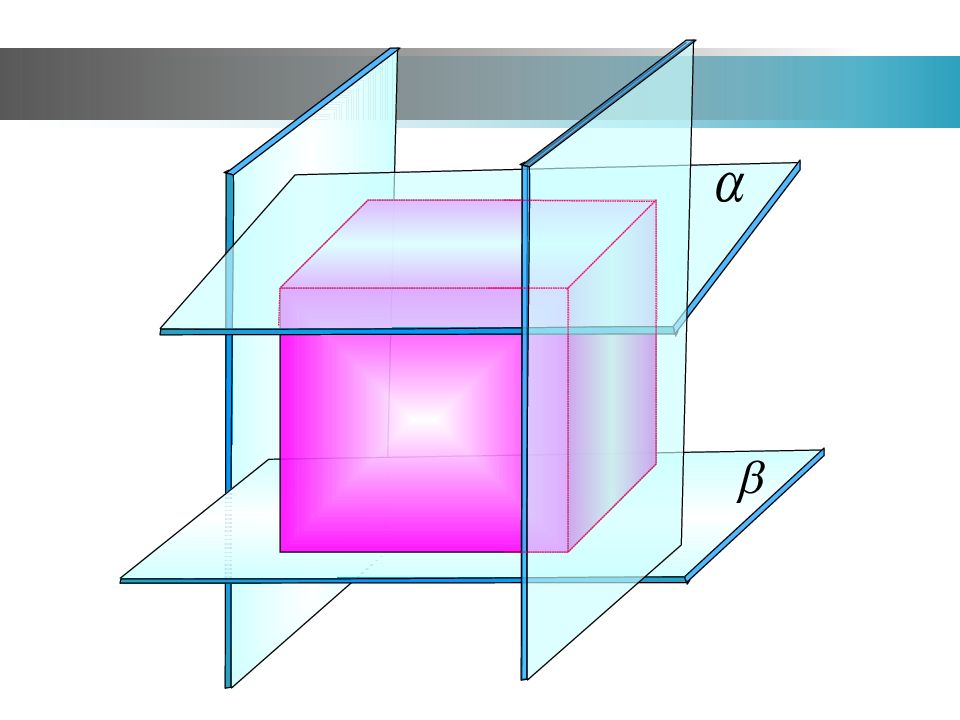
Две плоскости называются параллельными, если они не пересекаются α β α ‖ β
Слайд 4: Признак параллельности плоскостей
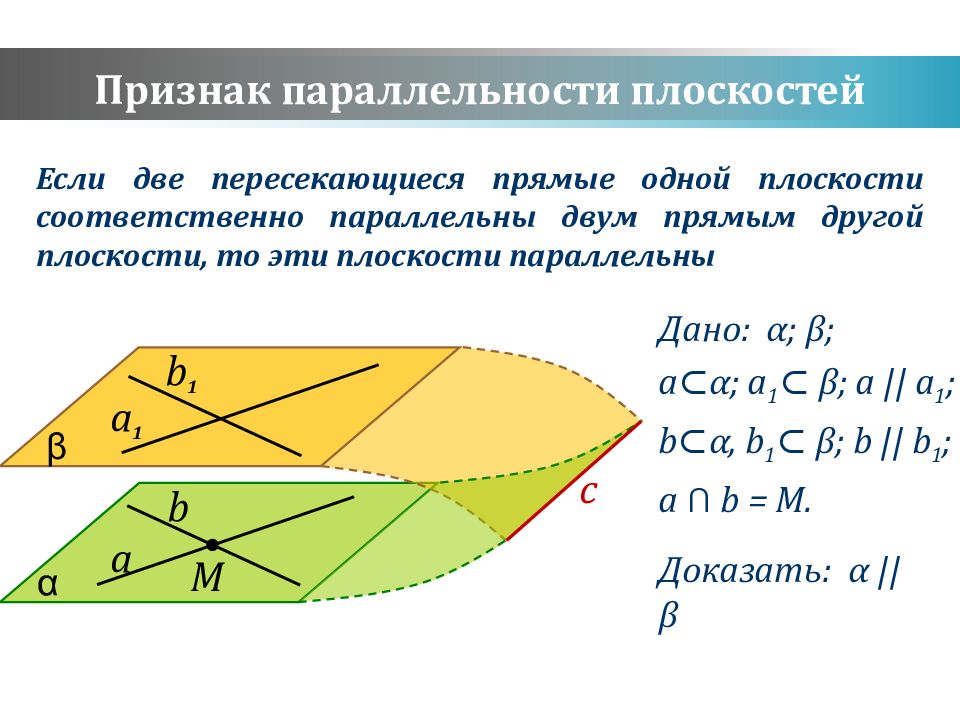
a b α b 1 a 1 β Дано: α ; β ; a⊂ α ; a 1 ⊂ β ; a || a 1 ; b ⊂ α, b 1 ⊂ β ; b || b 1 ; a ⋂ b = M. Доказать: α || β М с Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны
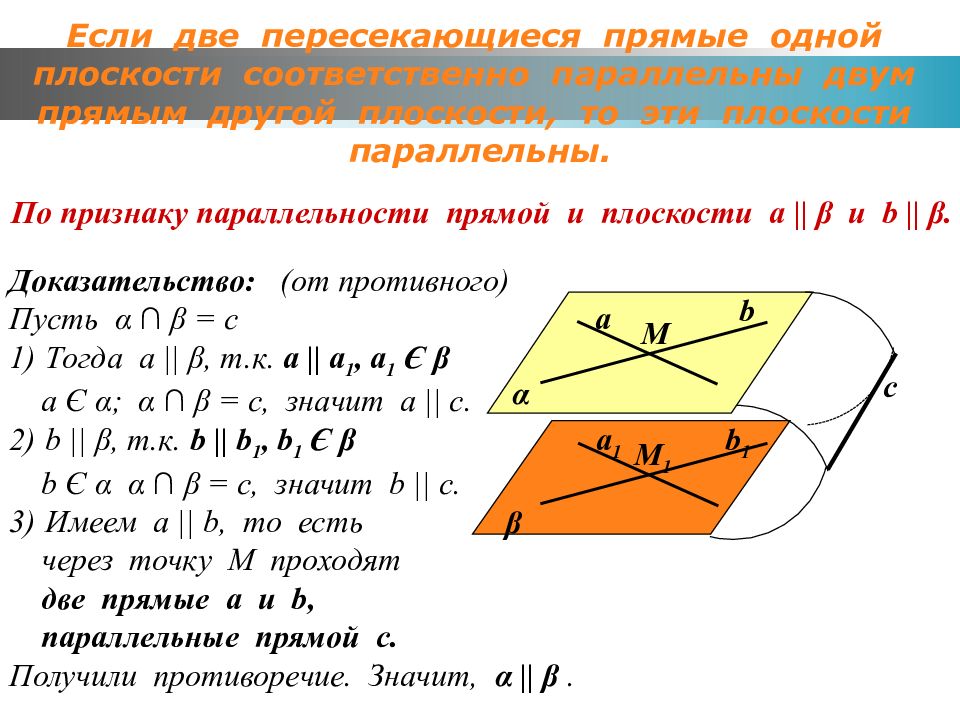
Доказательство: (от противного) Пусть α ∩ β = с Тогда а || β, т.к. a || a 1, а 1 Є β а Є α ; α ∩ β = с, значит а || с. b || β, т.к. b || b 1, b 1 Є β b Є α α ∩ β = с, значит b || с. Имеем а || b, то есть через точку М проходят две прямые а и b, параллельные прямой с. Получили противоречие. Значит, α || β. α β а b М b 1 а 1 М 1 с По признаку параллельности прямой и плоскости а || β и b || β.
Слайд 9: Параллельные плоскости в природе
Если стоять спиной к водопаду, скалы образуют геометрически правильные параллельные плоскости
Слайд 11: Параллельные плоскости в быту
В своей сущности и основе геометрия –это пространственное воображение, пронизанное и организованное строгой логикой В ней всегда присутствуют эти два неразрывно связанных элемента: наглядная картина и точная формулировка, строгий логический вывод. Там, где нет одной из этих сторон, нет и подлинной геометрии.
Слайд 12: Параллельные плоскости в искусстве
Д.Грин «Мечты» Силуэты мальчика расположены в параллельных плоскостях
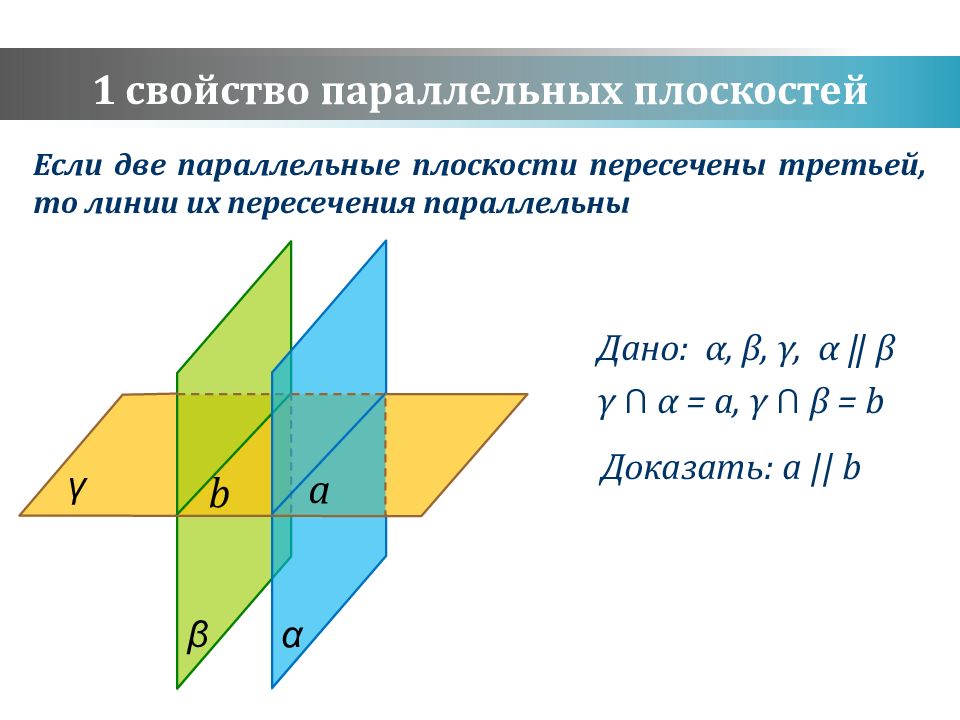
Слайд 13: 1 свойство параллельных плоскостей
Дано: α, β, γ, α ‖ β γ ⋂ α = a, γ ⋂ β = b Доказать: a || b Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны 1 свойство параллельных плоскостей β α γ b a
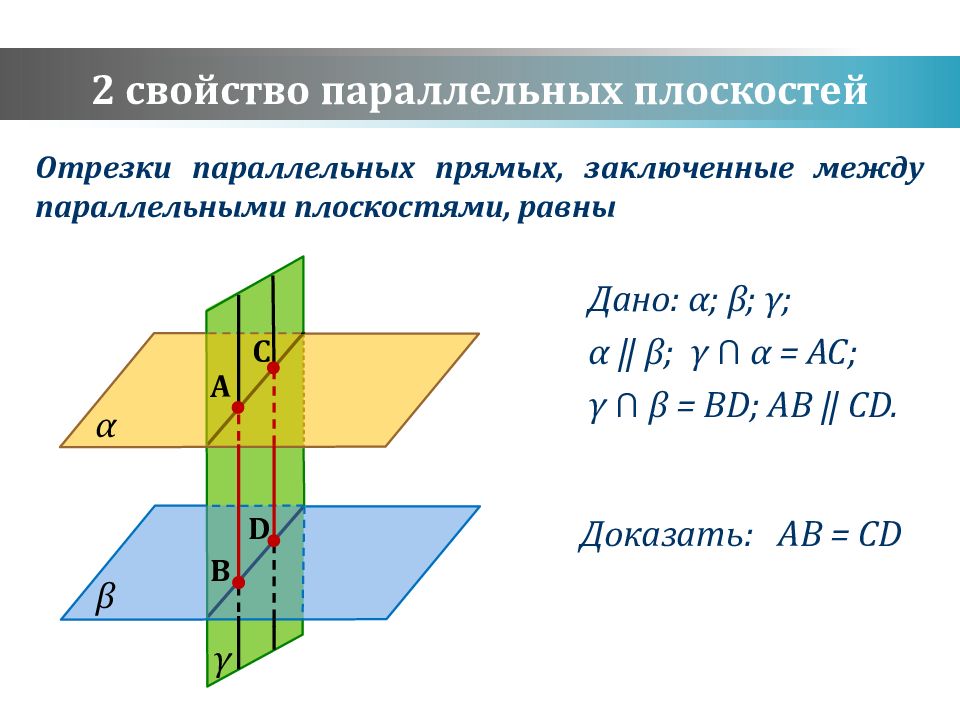
Слайд 14: 2 свойство параллельных плоскостей
Дано: α ; β ; γ ; α ‖ β ; γ ⋂ α = AC; γ ⋂ β = BD; AB ‖ CD. Доказать: AB = CD Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны 2 свойство параллельных плоскостей γ B D A C α β
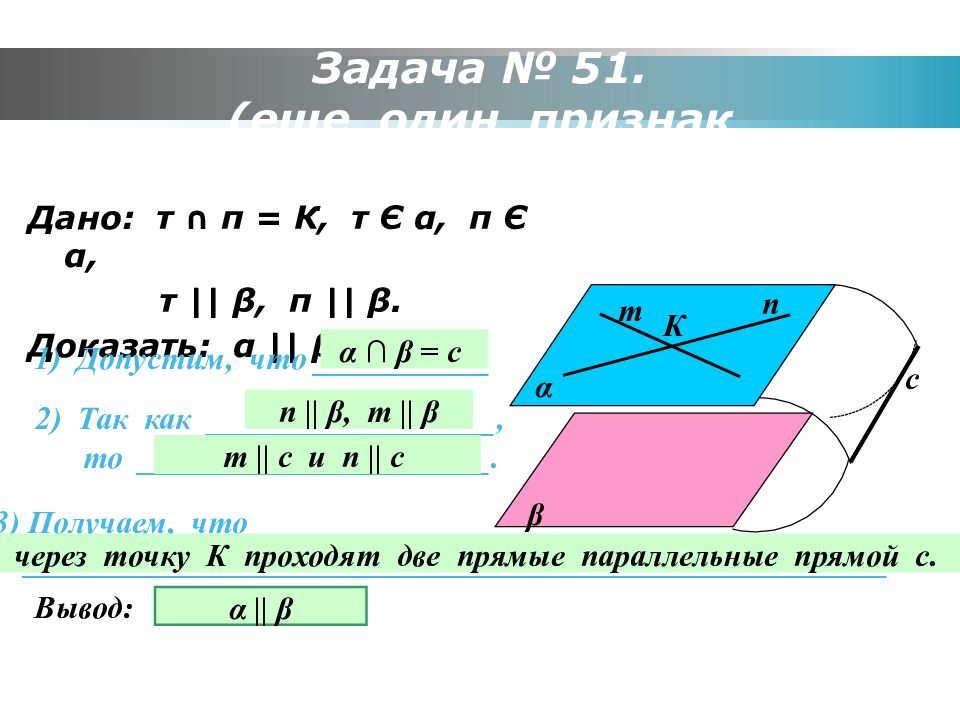
Слайд 15: Задача № 51. (еще один признак параллельности)
Дано: т ∩ п = К, т Є α, п Є α, т || β, п || β. Доказать: α || β. α β т п К с 1) Допустим, что ___________ 2) Так как __________________, то ______________________. Получаем, что ______________________________________________________. Вывод: α ∩ β = с п || β, т || β т || с и п || с через точку К проходят две прямые параллельные прямой с. α || β
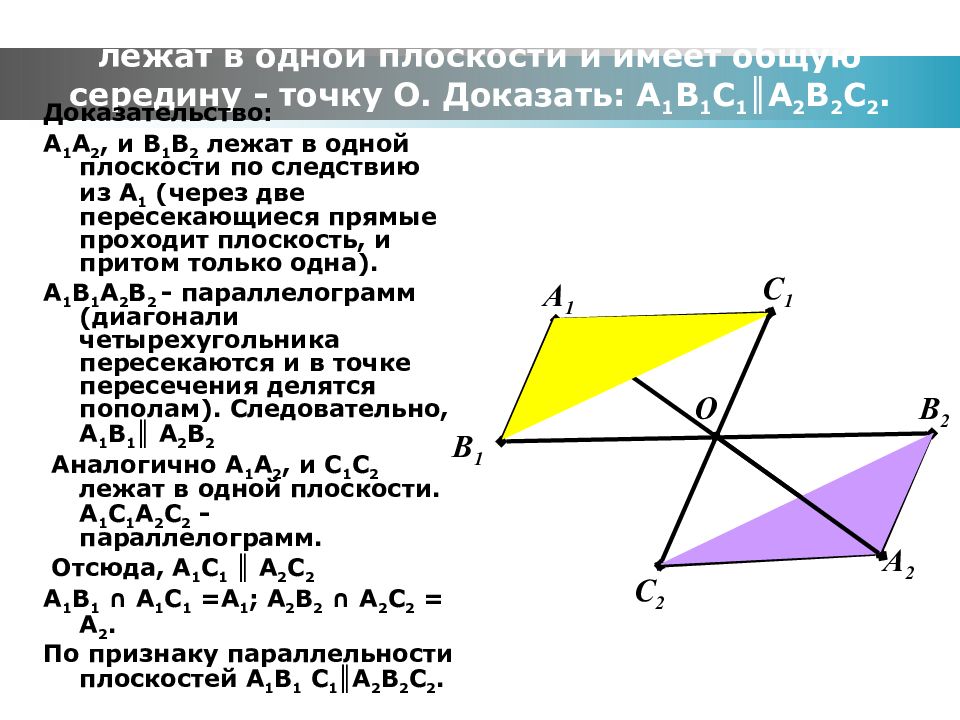
Слайд 16: Задача № 53. Дано: отрезки А 1 А 2, В 1 В 2, С 1 С 2 не лежат в одной плоскости и имеет общую середину - точку О. Доказать: А 1 В 1 С 1 ║А 2 В 2 С 2
Доказательство: А 1 А 2, и В 1 В 2 лежат в одной плоскости по следствию из А 1 (через две пересекающиеся прямые проходит плоскость, и притом только одна). А 1 В 1 А 2 В 2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А 1 В 1 ║ А 2 В 2 Аналогично А 1 А 2, и С 1 С 2 лежат в одной плоскости. А 1 С 1 А 2 С 2 - параллелограмм. Отсюда, А 1 С 1 ║ А 2 С 2 А 1 В 1 ∩ А 1 С 1 =А 1 ; А 2 В 2 ∩ А 2 С 2 = А 2. По признаку параллельности плоскостей А 1 В 1 С 1 ║А 2 В 2 С 2. А 1 В 1 А 2 В 2 С 2 С 1 О
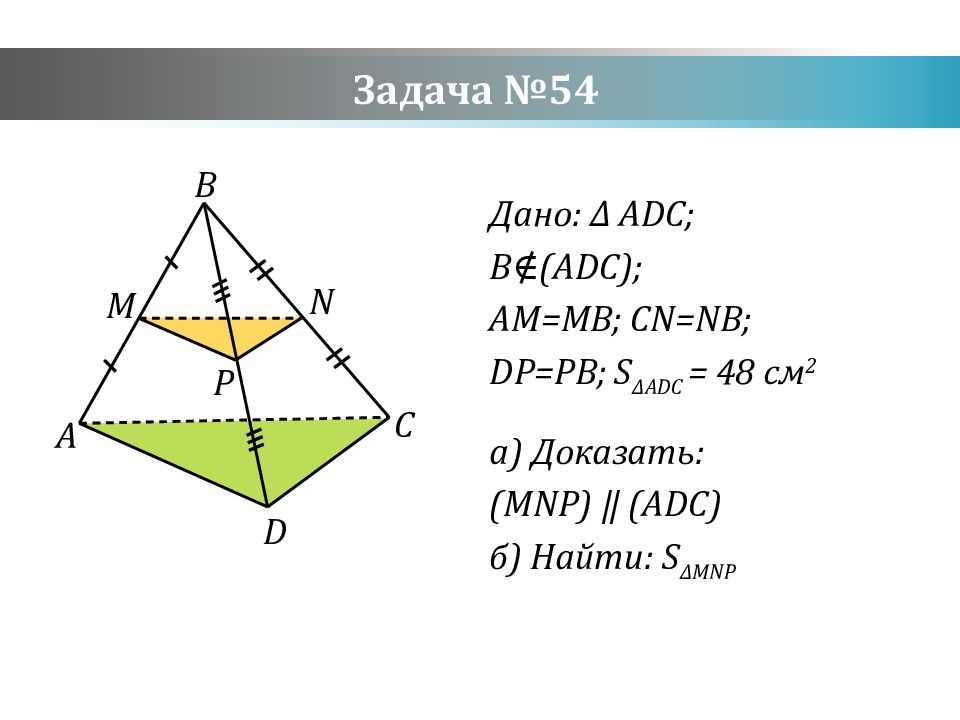
Слайд 17: Задача №54
Дано : ∆ ADC; B ∉(ADC); AM=MB; CN=NB; DP=PB ; S ∆ADC = 48 см 2 а) Доказать: ( MNP) ‖ (ADC) б) Найти: S ∆ MNP A D C B M N P
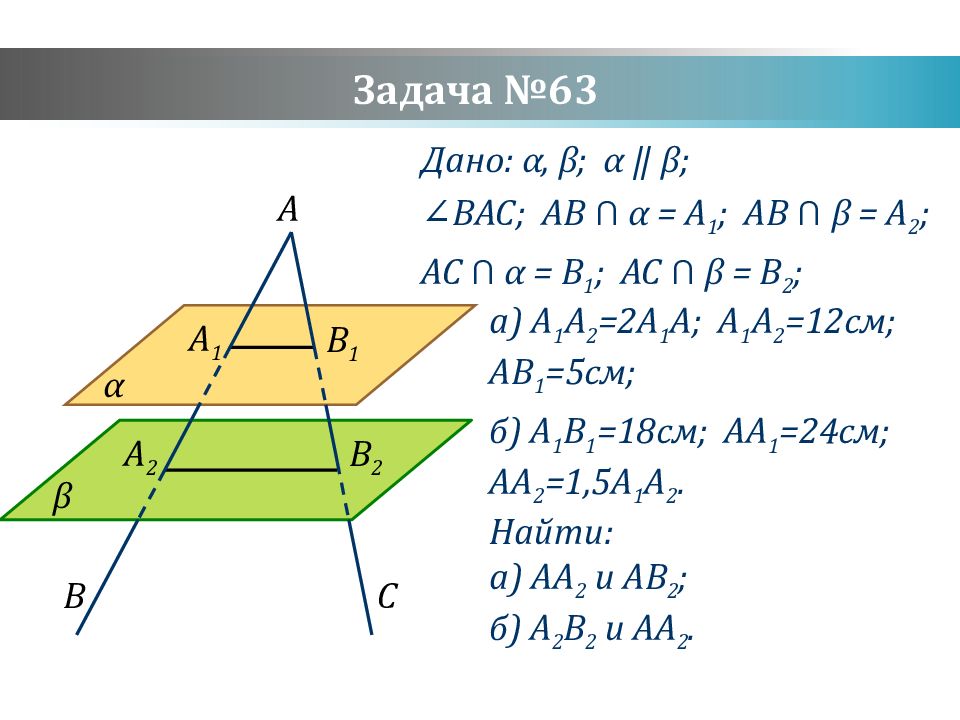
Слайд 18: Задача №63
Дано: α, β ; α ‖ β ; ∠BAC ; AB ⋂ α = A 1 ; AB ⋂ β = A 2 ; AC ⋂ α = B 1 ; AC ⋂ β = B 2 ; Найти: а ) AA 2 и AB 2 ; б ) A 2 B 2 и AA 2. а) A 1 A 2 =2A 1 A ; A 1 A 2 =12 см; AB 1 =5 см; б) A 1 B 1 =18 см; AA 1 =24 см; AA 2 =1,5A 1 A 2. α β B A C A 1 A 2 B 2 B 1
Слайд 19: Отвечаем на вопросы
Могут ли прямая и плоскость не иметь общих точек? Верно ли, что если две прямые не пересекаются, то они параллельны? Плоскости и β параллельны, прямая m не лежит в плоскости . Верно ли, что прямая m параллельна плоскости β? Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку? Боковые стороны трапеции параллельны плоскости . Верно ли, что плоскость трапеции параллельна плоскости ? Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции? Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости? Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей? Верно ли, что любые четыре точки лежат в одной плоскости? Верно ли, что если две стороны треугольника параллельны плоскости , то и третья сторона параллельна плоскости ?
Слайд 20: Проверяем свою работу
Могут ли прямая и плоскость не иметь общих точек? Да Верно ли, что если две прямые не пересекаются, то они параллельны? Нет Плоскости и β параллельны, прямая m не лежит в плоскости . Верно ли, что прямая m параллельна плоскости β? Да Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку? Нет Боковые стороны трапеции параллельны плоскости . Верно ли, что плоскость трапеции параллельна плоскости ? Да Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции? Нет Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости? Нет Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей? Нет Верно ли, что любые четыре точки лежат в одной плоскости? Нет Верно ли, что если две стороны треугольника параллельны плоскости , то и третья сторона параллельна плоскости ? Да