Параллельность прямой и плоскости Геометрия 10
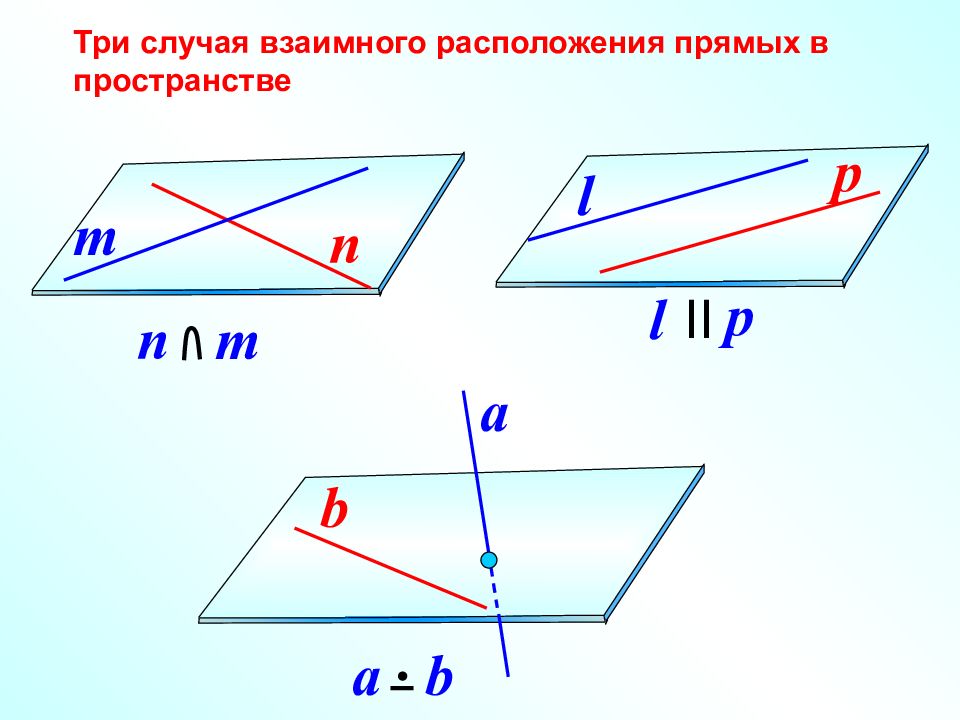
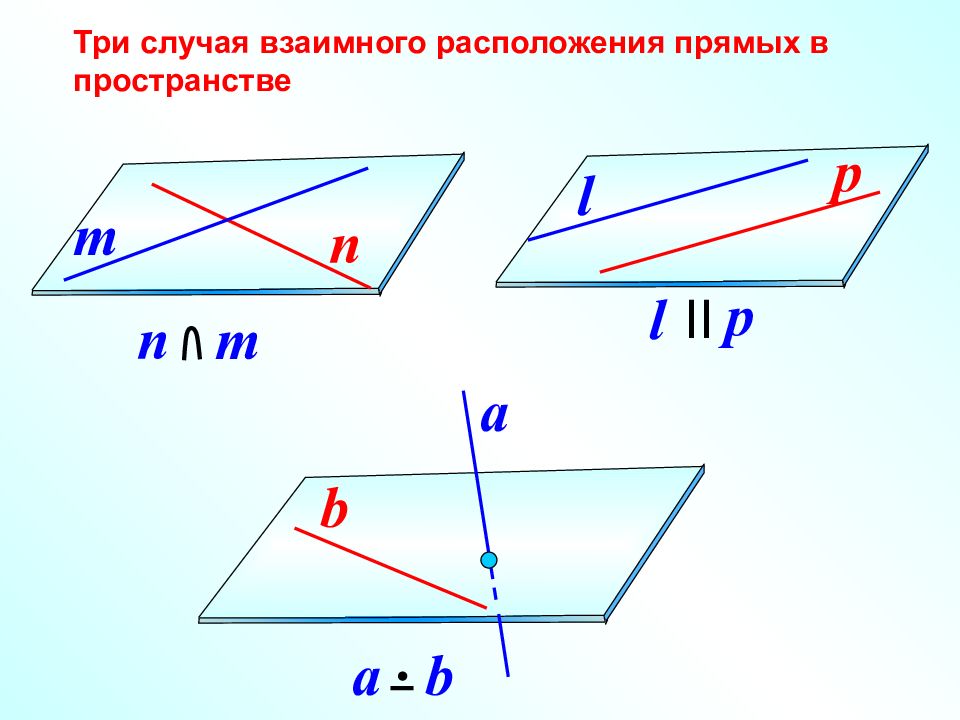
b a b Три случая взаимного расположения прямых в пространстве n m l p n m l p II a
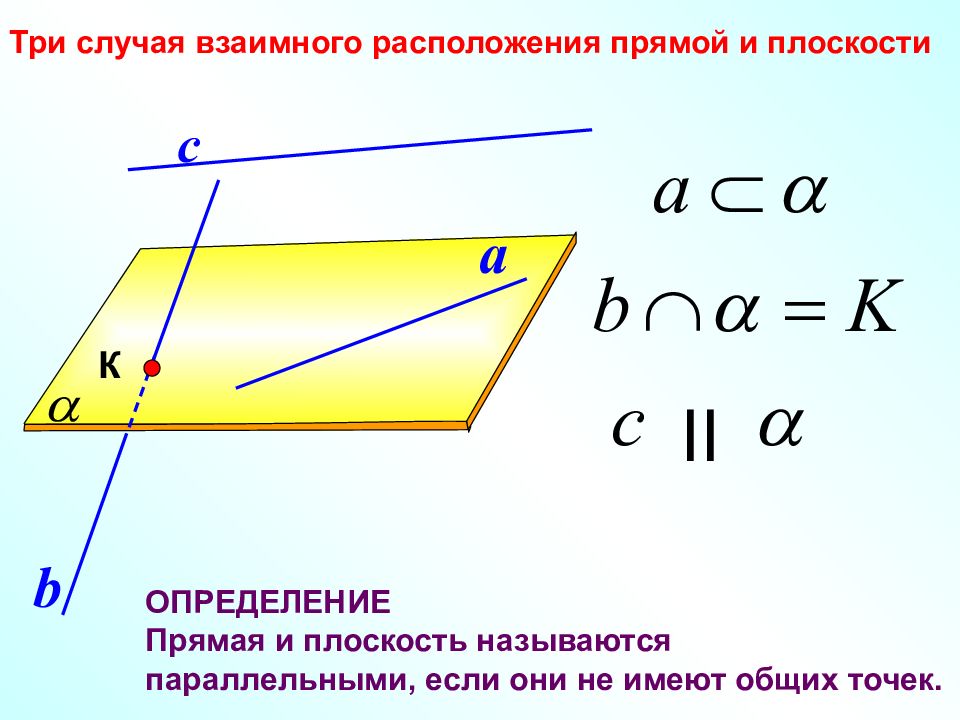
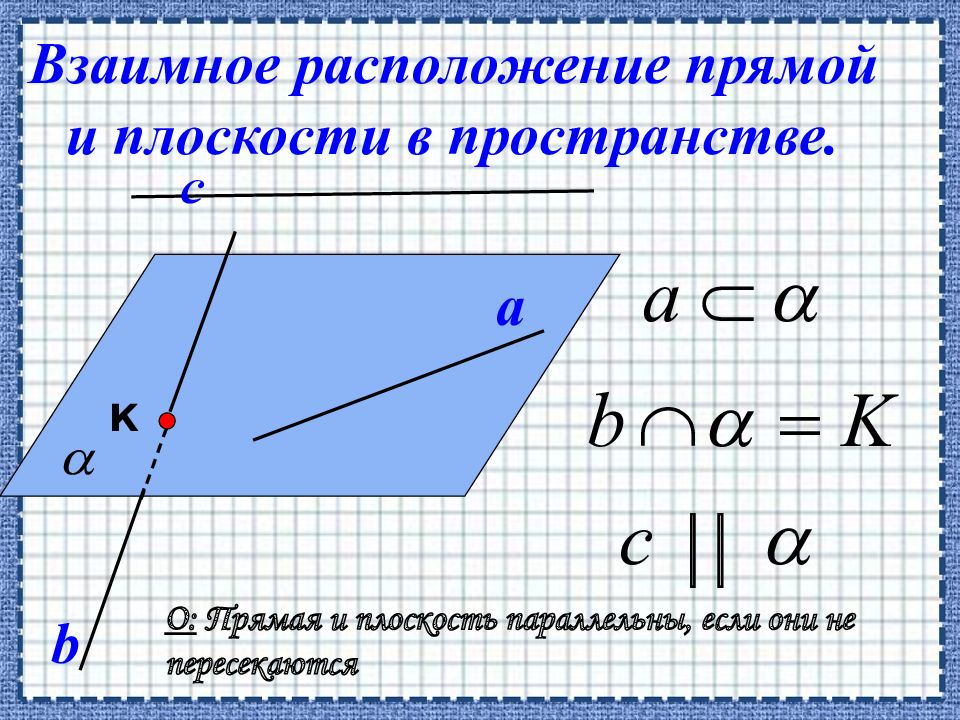
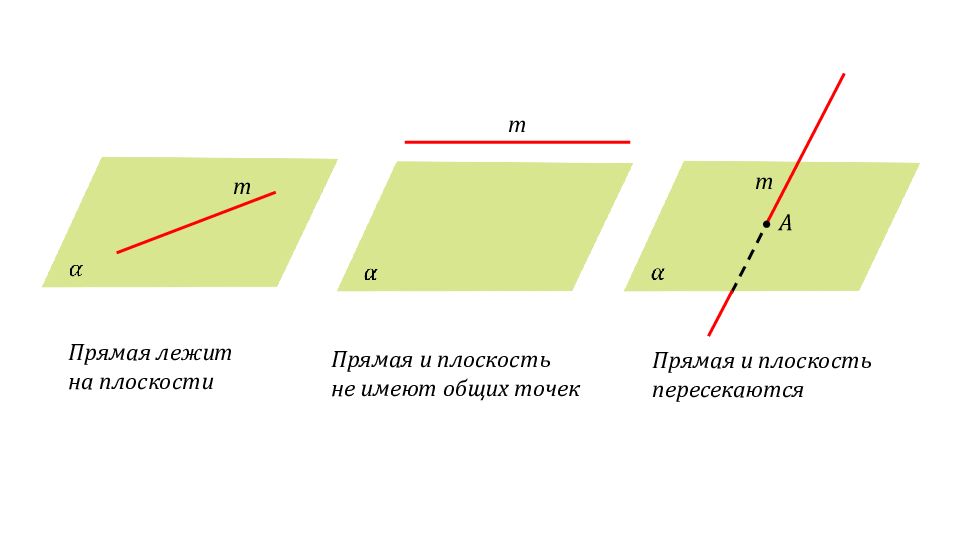
a с Три случая взаимного расположения прямой и плоскости II b К ОПРЕДЕЛЕНИЕ Прямая и плоскость называются параллельными, если они не имеют общих точек.
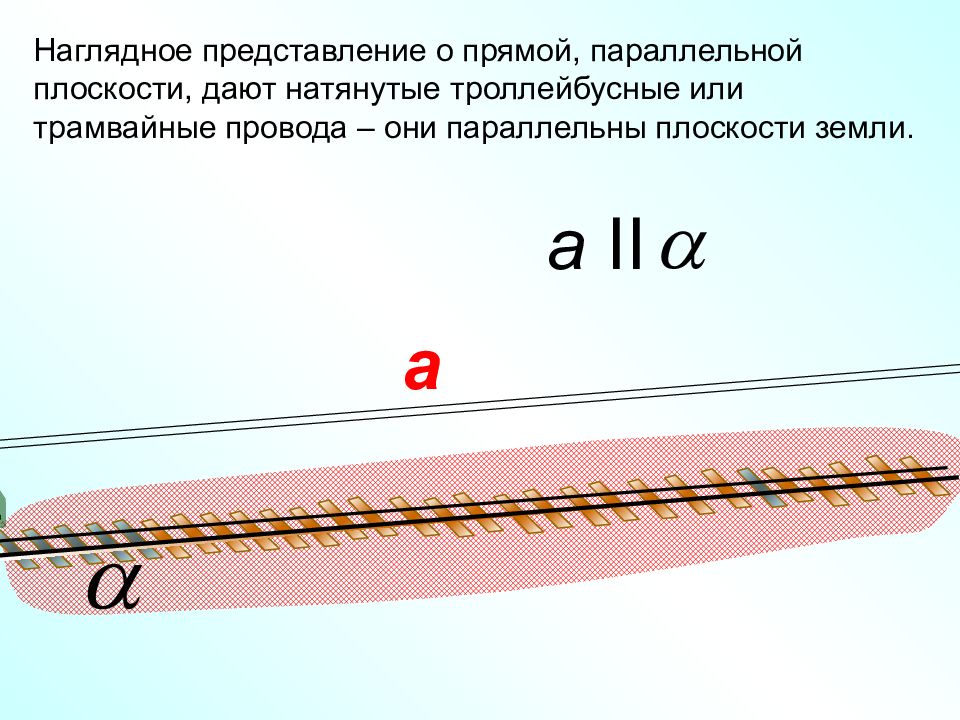
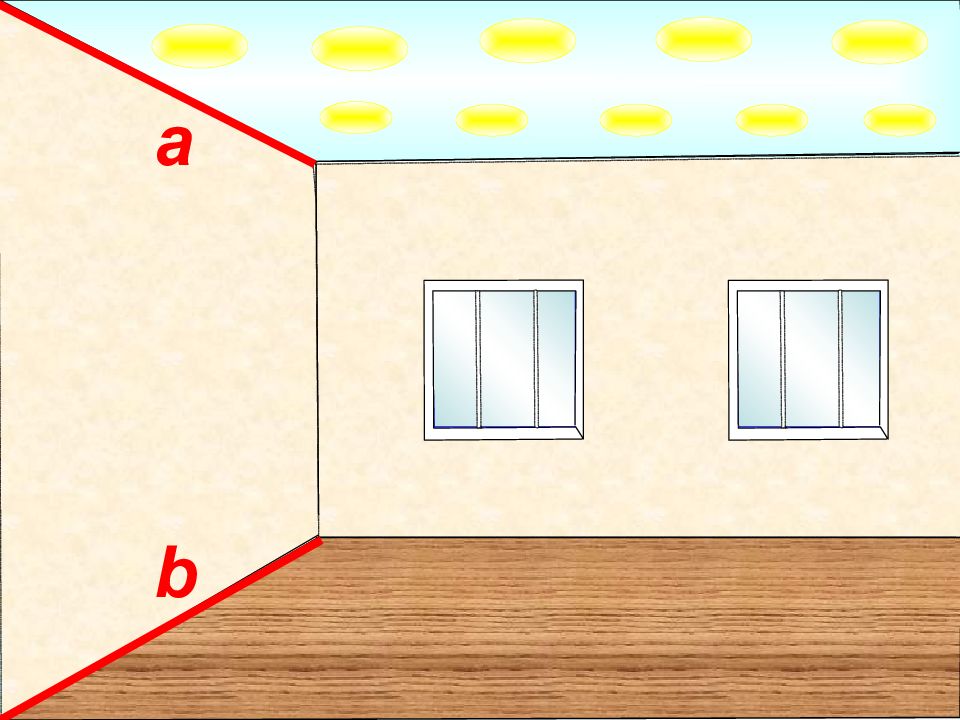
а a II Наглядное представление о прямой, параллельной плоскости, дают натянутые троллейбусные или трамвайные провода – они параллельны плоскости земли.
а
а b
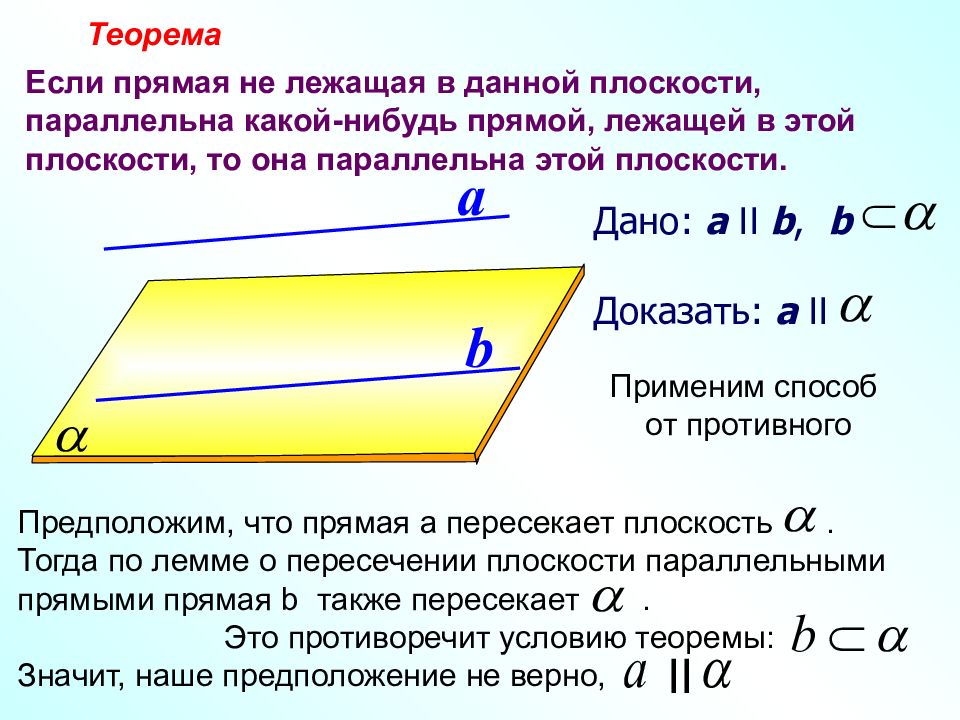
Дано: a II b, b Доказать: a II a b Теорема Если прямая не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна этой плоскости. Применим способ от противного Предположим, что прямая а пересекает плоскость. Тогда по лемме о пересечении плоскости параллельными прямыми прямая b также пересекает. Это противоречит условию теоремы: Значит, наше предположение не верно, II
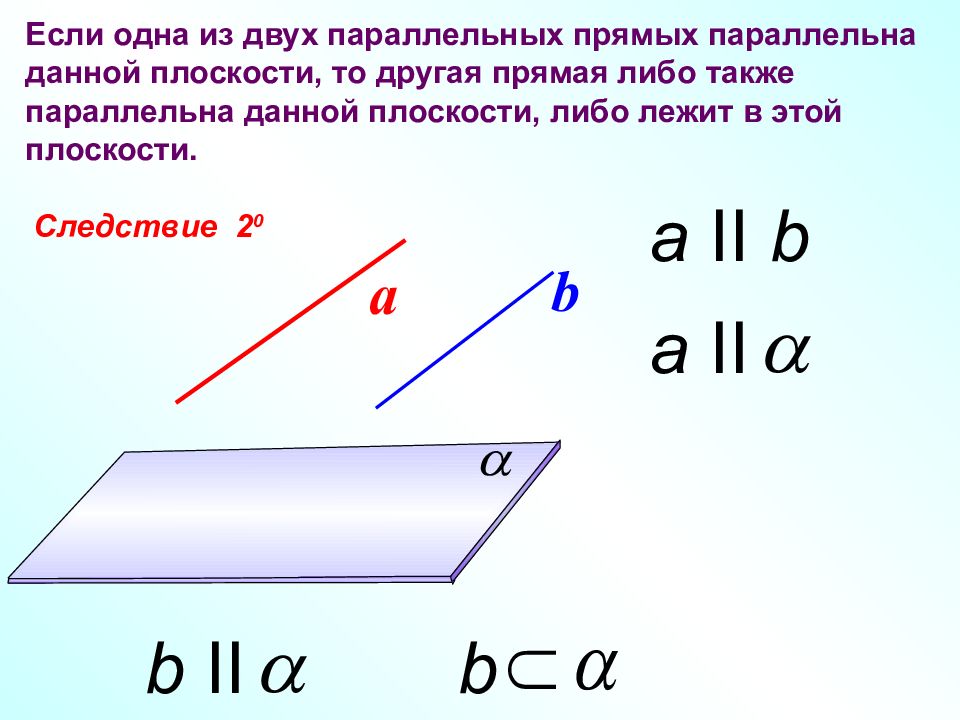
Следствие 1 0 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. b a a II b II a a II
Следствие 2 0 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. а b a II b a II b II b
