Применение математических функций в жизни человека и различных науках
Франсуа Виет (1540 – 1603гг.) История развития понятия функции в XVII веке Рене Декарт (1596-1650гг.) Пьер Ферма (1602-1665гг.)
Декарт Рене, Франсуа Виет Декарт Рене, Ферма Пьер Декарт Рене - понятие функции представление кривых в виде уравнений единая буквенная математическая символика: x, y, z, a, b, c,.. и т. д переменная величина прямоугольная система координат Основные понятия:
Готфрид Вильгельм фон Лейбниц Функция (от лат. Functio – совершение, выполнение ) – отрезок, длина которого меняется по какому- нибудь определенному закону. – впервые ввёл термины «константа» и «переменная» Аналитическое определение функции
Основные понятия: применил знак для х- (х) - впервые сделал подход к аналитической функции Иоганн Бернулли Леонард Эйлер Основные понятия: - вывел окончательную формулировку определения: функция переменного количества есть аналитическое выражение, составленное каким либо способом из этого количества и чисел или постоянных количеств.
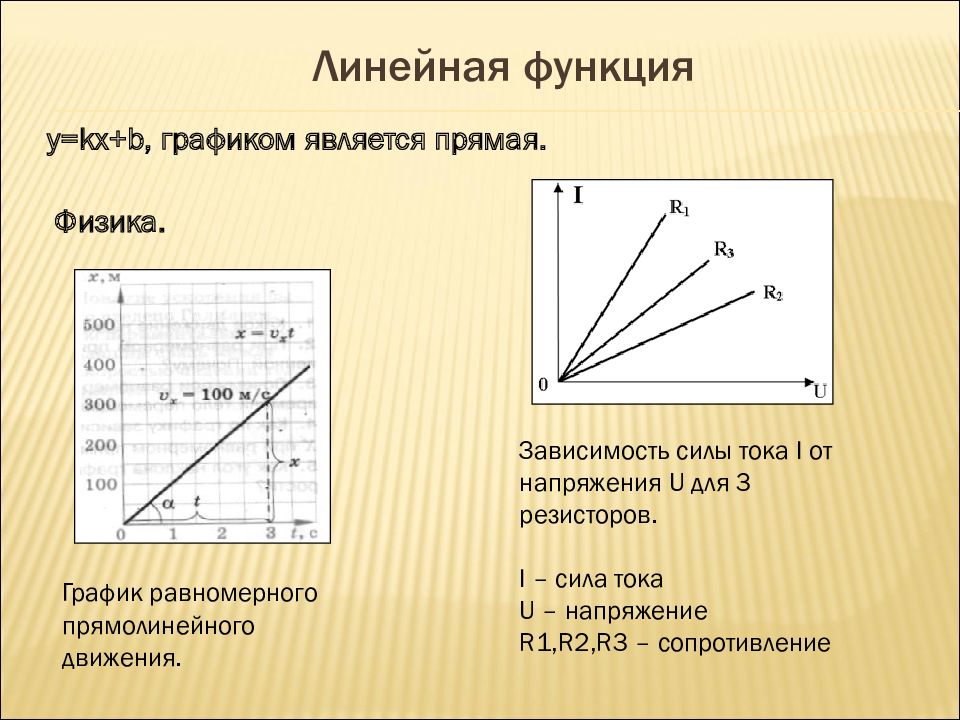
График равномерного прямолинейного движения. Физика. Зависимость силы тока I от напряжения U для 3 резисторов. I – c ила тока U – напряжение R1,R2,R3 – сопротивление y=kx+b, графиком является прямая.
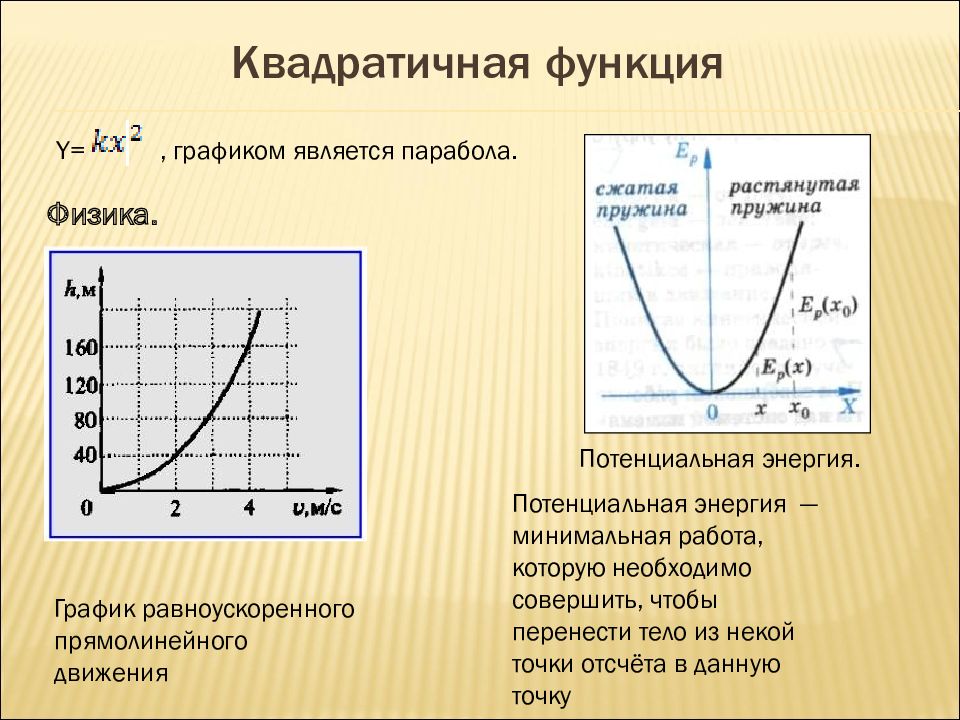
График равноускоренного прямолинейного движения Физика. Потенциальная энергия. Y=, графиком является парабола. Потенциальная энергия — минимальная работа, которую необходимо совершить, чтобы перенести тело из некой точки отсчёта в данную точку
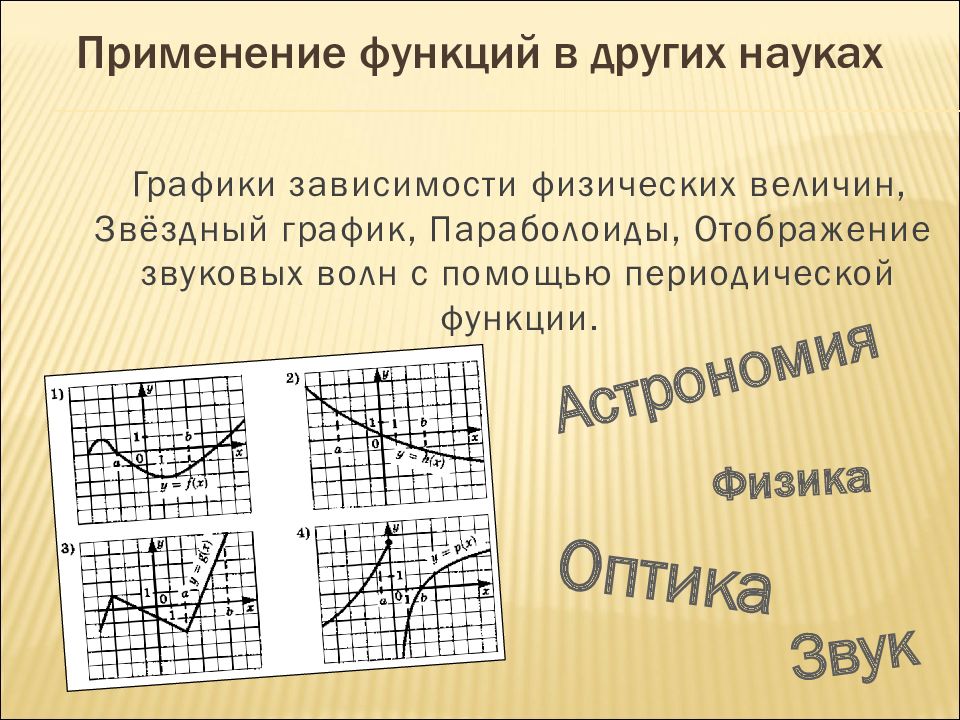
Физика Астрономия Звук Графики зависимости физических величин, Звёздный график, Параболоиды, Отображение звуковых волн с помощью периодической функции. Оптика
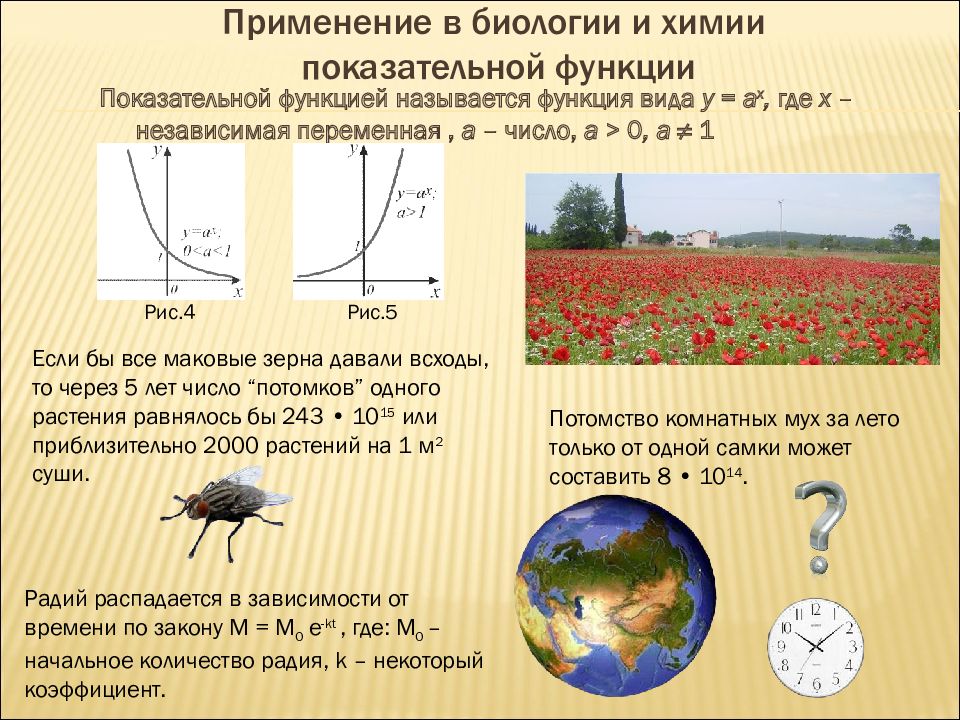
Показательной функцией называется функция вида у = a x, где х – независимая переменная, a – число, a > 0, a ≠ 1 Если бы все маковые зерна давали всходы, то через 5 лет число “потомков” одного растения равнялось бы 243 • 10 15 или приблизительно 2000 растений на 1 м 2 суши. Потомство комнатных мух за лето только от одной самки может составить 8 • 10 14. Радий распадается в зависимости от времени по закону М = М 0 e -kt, где: М 0 – начальное количество радия, k – некоторый коэффициент. Рис.4 Рис.5
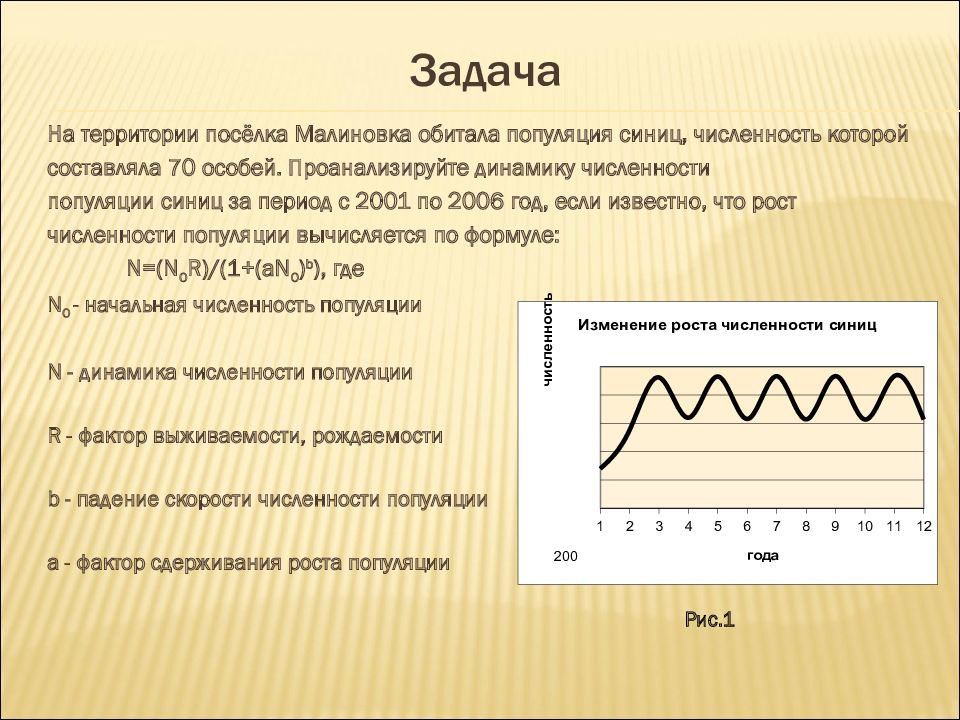
На территории посёлка Малиновка обитала популяция синиц, численность которой составляла 70 особей. Проанализируйте динамику численности популяции синиц за период с 2001 по 2006 год, если известно, что рост численности популяции вычисляется по формуле: N=(N 0 R)/(1+(aN 0 ) b ), где N 0 - начальная численность популяции N - динамика численности популяции R - фактор выживаемости, рождаемости b - падение скорости численности популяции a - фактор сдерживания роста популяции Рис.1 200
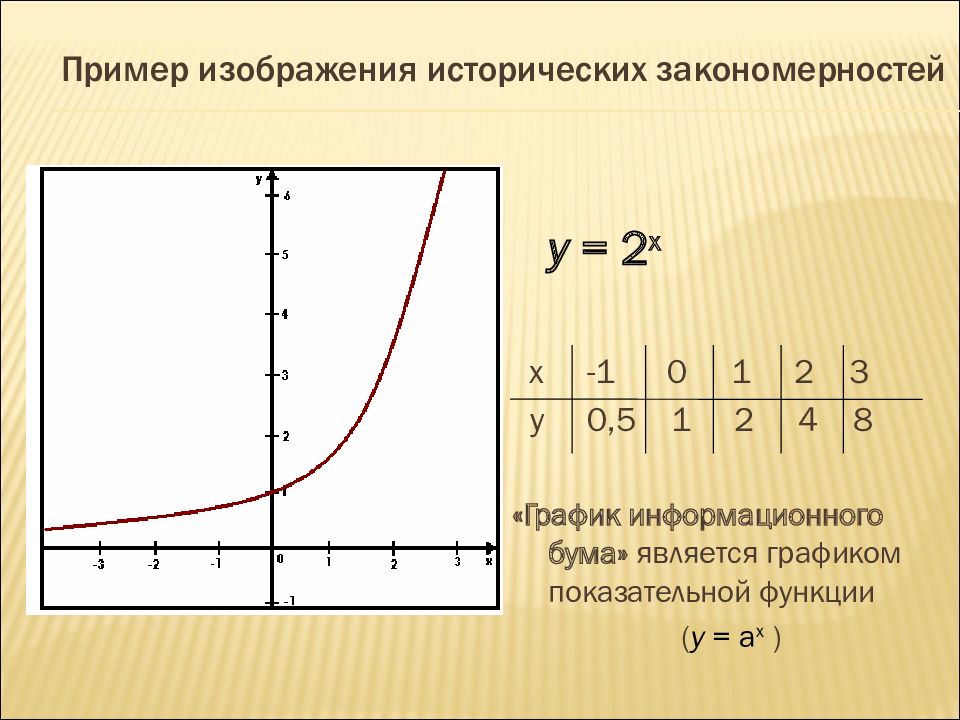
y = 2 x x -1 0 1 2 3 y 0,5 1 2 4 8 «График информационного бума» является графиком показательной функции ( y = a x )
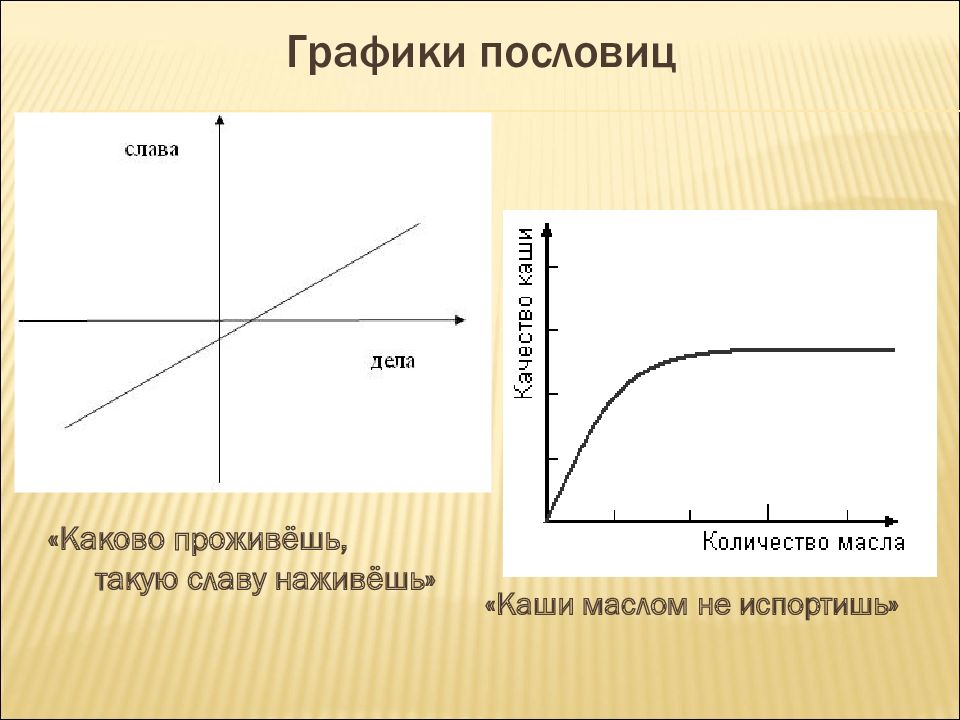
«Каши маслом не испортишь» «Каково проживёшь, такую славу наживёшь»
