a α c b
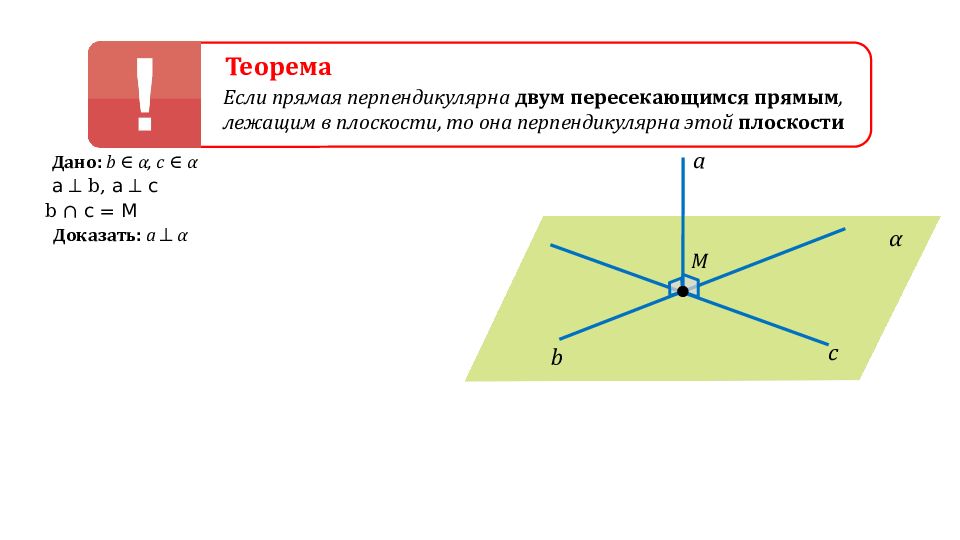
Дано: b ∈ α, с ∈ α а ⏊ b, а ⏊ с b ∩ с = М Доказать: а ⏊ α a α c b M Теорема Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости
a α c b Доказательство: 1) х ∈ α 2) у ∥ х, у ∈ α, М ∈ у M x у 3) М 1 М 2 ∈ а, М 1 М = ММ 2 М 1 М 2 4) ВС ∈ α, ВС ∩ c = C, ВС ∩ b = В, ВС ∩ у = Y B Y C Теорема Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости Дано: b ∈ α, с ∈ α а ⏊ b, а ⏊ с b ∩ с = М Доказать: а ⏊ α 6) ∆ВМ 1 М = ∆ВМ 2 М: ВМ 1 = ВМ 2, СМ 1 = СМ 2, ВМ — общая 8 ) M 1 Y = YM 2 ⇒ ∆ М 1 Y М 2 – равноб. 9 ) Y М ⏊ М 1 М 2 ⇒ y ⏊ a ⇒ ∠М 1 ВY = ∠М 2 ВY ВМ 1 = ВМ 2, СМ 1 = СМ 2 6) ∆М 1 В Y = ∆М 2 В Y : ВМ 1 = ВМ 2, В Y — общая, ∠М 1 ВY = ∠М 2 ВY ⇒ М 1 Y = М 2 Y
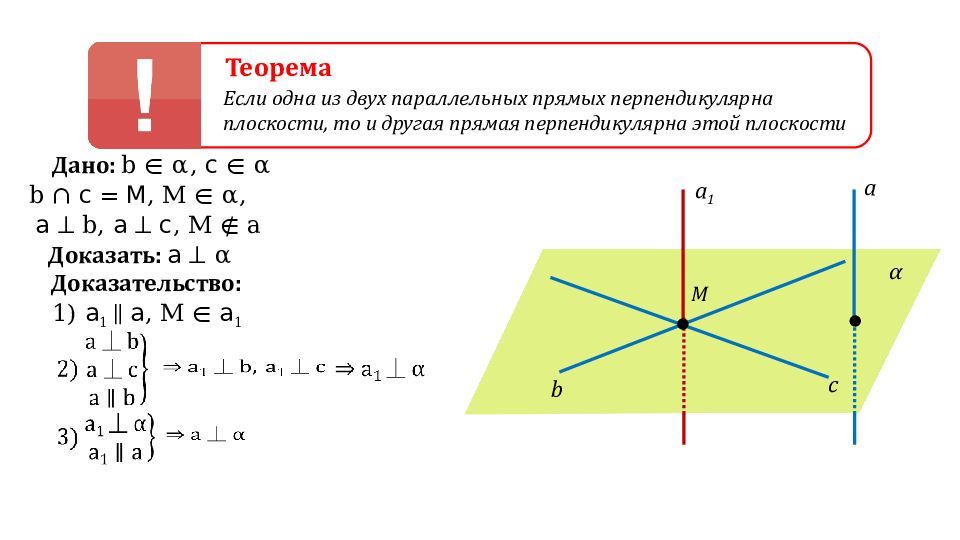
Теорема Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости Дано: b ∈ α, с ∈ α b ∩ с = М, M ∈ α, а ⏊ b, а ⏊ с, M ∉ a Доказать: а ⏊ α a α c b M Доказательство: 1) а 1 ∥ а, M ∈ а 1 а 1
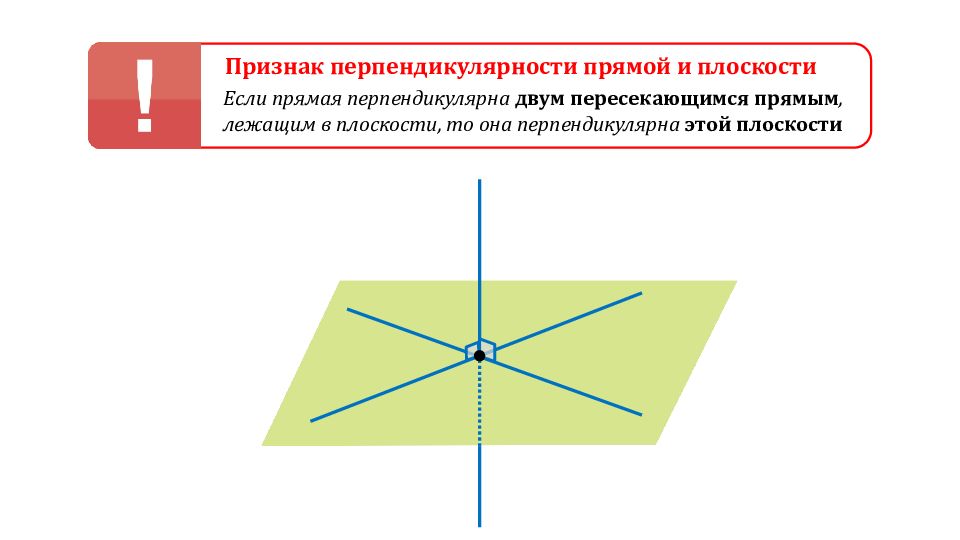
Признак перпендикулярности прямой и плоскости Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости
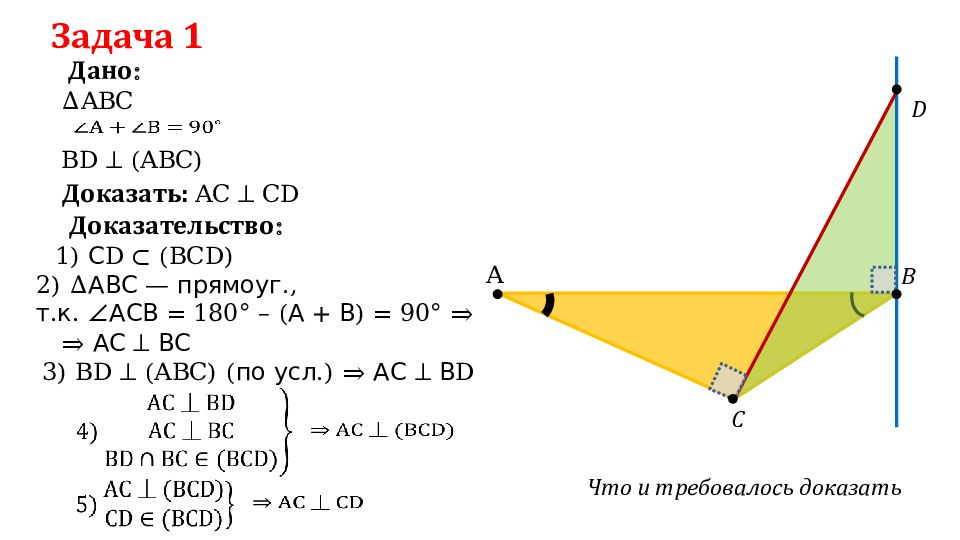
Задача 1 ∆ ABC Дано : Доказать: AC ⏊ CD Доказательство : 1) С D ⊂ (BCD) 2) ∆ АВС — прямоуг., т.к. ∠АСВ = 180° – (А + В) = 90° ⇒ Что и требовалось доказать BD ⏊ (ABC) A B C D 3) BD ⏊ (ABC) ( по усл. ) ⇒ АС ⏊ В D ⇒ АС ⏊ ВС
Задача 2 АВС D и АВ EF — квадраты Дано: AD ⏊ AF Доказать: B С ⏊ (AEF) Доказательство: 1) АВ EF — квадрат ⇒ AB ⏊ AF Что и требовалось доказать A B C E F D ⇒ BC ⏊ (AEF)
