Общее уравнение прямой Уравнение прямой в отрезках Каноническое уравнение прямой Уравнение прямой с угловым коэффициентом Угол между двумя прямыми Расстояние от точки до прямой Биссектриса углов между прямыми Деление отрезка в заданном отношении
М 0 (х 0 ; у 0 ) Уравнение вида: Теорема с произвольными коэффициентами А; В; С такими, что А и В не равны нулю одновременно, называется общим уравнением прямой. Если точка М 0 (х 0 ; у 0 ) принадлежит прямой, то общее уравнение прямой превращается в тождество: Пусть задана прямая: Вектор будет ортогонален этой прямой. Доказательство: Пусть некоторая точка М 0 (х 0 ; у 0 ) принадлежит прямой: (1) (2)
Найдем разность уравнений (1) и (2) : Пусть точки М 0 (х 0 ; у 0 ) и М (х; у ) лежат на данной прямой. (3) М 0 (х 0 ; у 0 ) М (х; у ) Рассмотрим векторы: и Равенство (3) представляет собой скалярное произведение этих векторов, которое равно нулю: Таким образом, вектор перпендикулярен прямой и называется нормальным вектором прямой. Равенство (3) также является общим уравнением прямой
Общее уравнение прямой называется полным, если все коэффициенты А, В, и С отличны от нуля. В противном случае уравнение называется неполным. 1) Виды неполных уравнений : y 0 х 2) 3) 4) 5)
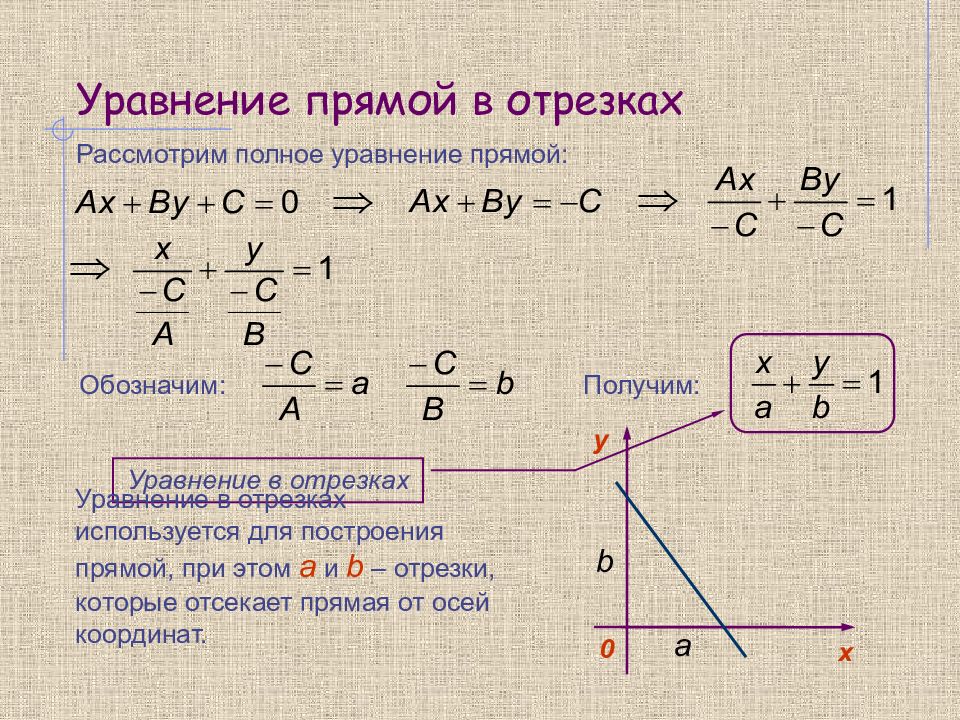
Рассмотрим полное уравнение прямой: Обозначим: Получим: Уравнение в отрезках y 0 х b a Уравнение в отрезках используется для построения прямой, при этом a и b – отрезки, которые отсекает прямая от осей координат.
Любой ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Требуется найти уравнение прямой, проходящей через заданную точку М 0 (х 0 ; у 0 ) и параллельно заданному вектору М 0 (х 0 ; у 0 ) М (х; у ) Очевидно, что точка М (х; у ) лежит на прямой, только в том случае, если векторы и коллинеарны. По условию коллинеарности получаем: Каноническое уравнение прямой
Пусть прямая проходит через две заданные и отличные друг от друга точки: М 1 (х 1 ; у 1 ) и М 2 (х 2 ; у 2 ). М 1 (х 1 ; у 1 ) М 2 (х 2 ; у 2 ) Тогда в качестве направляющего вектора в каноническом уравнении можно взять вектор: Уравнение прямой, проходящей через две заданные точки
y 0 х Если прямая не параллельна оси OY и имеет направляющий вектор, то угловой коэффициент k этой прямой равен тангенсу угла наклона прямой к оси OX. Уравнение прямой с угловым коэффициентом Уравнение прямой с угловым коэффициентом = b
Прямая проходит через точку М(1; 2 ) и имеет направляющий вектор : Написать : каноническое, общее уравнение прямой, уравнение прямой в отрезках, уравнение с угловым коэффициентом. Найти нормальный вектор прямой, отрезки, которые отсекает прямая от осей координат и угол, который составляет прямая с осью OX. 1. Каноническое уравнение : 2. Общее уравнение :
3. Уравнение в отрезках : 4. Уравнение с угловым коэффициентом : y 0 х М b a
Пусть две прямые L 1 и L 2 заданы общими уравнениями: Угол между этими прямыми определяется как угол между нормальными векторами к этим прямым:
Пусть две прямые L 1 и L 2 заданы каноническими уравнениями: Угол между этими прямыми определяется как угол между направляющими векторами к этим прямым:
Пусть две прямые L 1 и L 2 заданы уравнениями с угловыми коэффициентами: y 0 х
Пусть необходимо найти расстояние от точки М 0 (х 0 ; у 0 ) до прямой, заданной общим уравнением: М 0 (х 0 ; у 0 ) М 1 (х 1 ; у 1 ) Пусть М 1 (х 1 ; у 1 ) – основание перпендикуляра, опущенного из точки М 0 на прямую L. Найдем скалярное произведение векторов и Найдем скалярное произведение в координатной форме:
Точка М 1 (х 1 ; у 1 ) принадлежит прямой L, следовательно:
Пусть две прямые L 1 и L 2 заданы общими уравнениями: Если точка M(x; y) лежит на биссектрисе угла между прямыми, то расстояние от точки М до прямой L 1 равна расстоянию до прямой L 2 : M(x; y)
Разделить отрезок М 1 М 2 в заданном отношении λ > 0 значит найти на отрезке такую точку М(х ;y ), что имеет место равенство: M 2 M 1 M или Пусть M 1 (x 1 ; y 1 ) и M 2 (x 2 ; y 2 ). Найдем координаты точки М. В координатной форме:
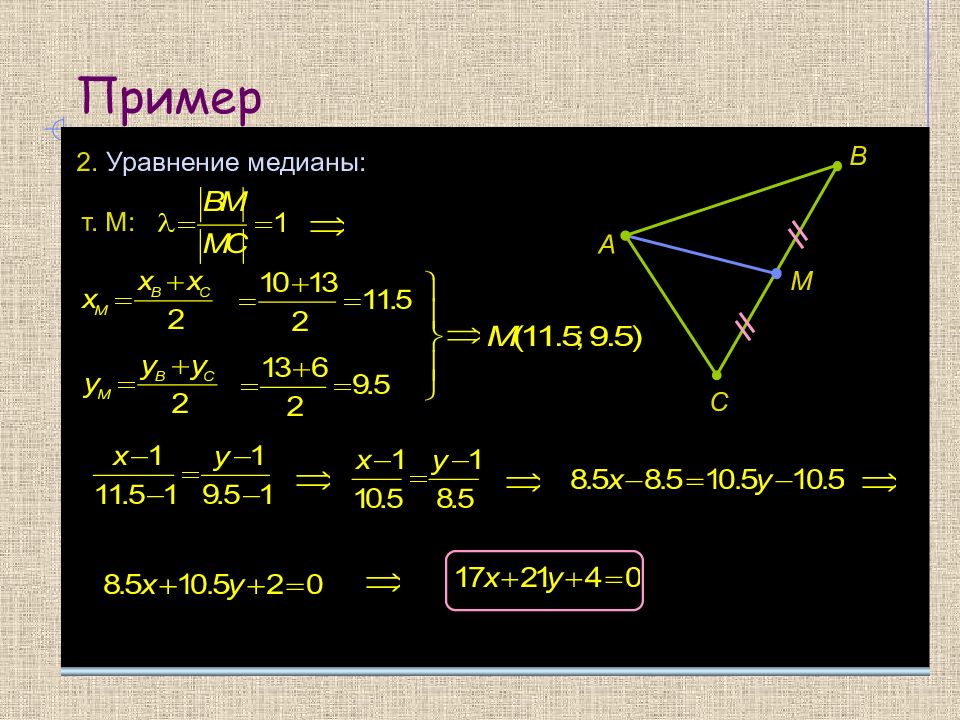
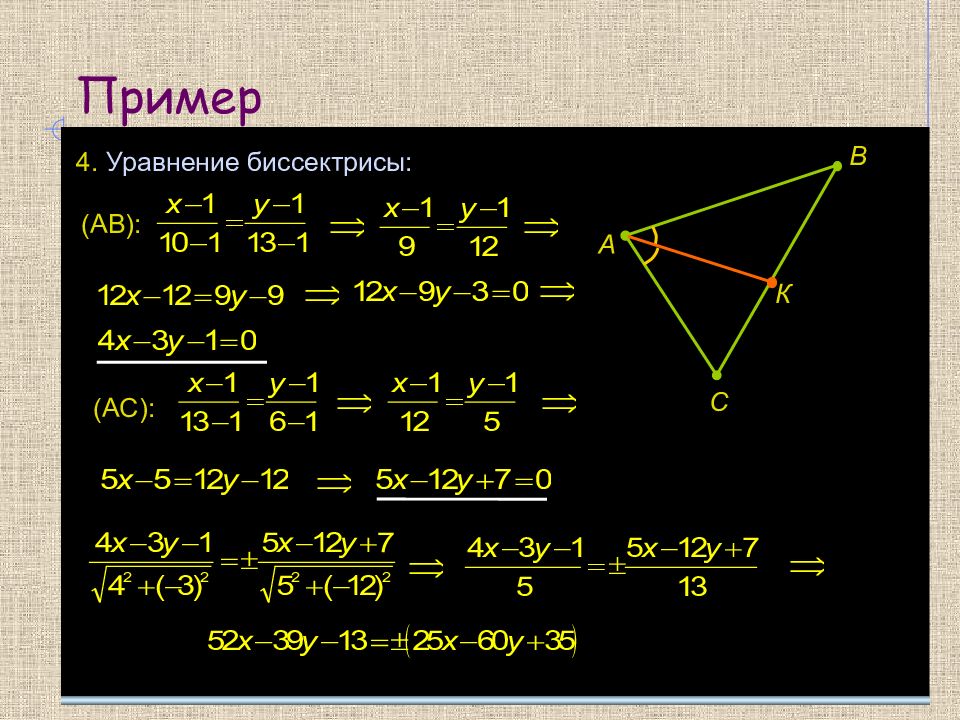
Даны вершины треугольника : А(1; 1); В(10; 13); С(13; 6) Найти : Уравнения высоты, медианы и биссектрисы, проведенных из вершины А. 1. Уравнение высоты: А В С Н (ВС): (АН):
2. Уравнение медианы: А В С М т. М:
4. Уравнение биссектрисы: А В С К (АВ): (АС):
Для биссектрисы внутреннего угла треугольника должно выполняться условие: или 1) 2)
