Первый слайд презентации: Презентация на тему: Виды матриц и их свойства
Выполнили: Кульчицкая Е.А. И Артюхова Д.С.
Слайд 2
Под матрицей понимается прямоугольный массив чисел, называемых элементами. Матрицы имеют длинную историю исследований и приложений, что приводит к различным способам их классификации. Первая группа матриц удовлетворяет конкретным условиям и ограничениям на их элементы, включая постоянные матрицы. Важный пример матриц такого вида доставляет единичная матрица: Обозначается также буквой E. Другие способы классификации матриц связаны либо с их собственными значениями, либо с условиями в виде матричных уравнений (соотношений). Наконец, во многих областях (в физике и в химии) встречаются матрицы специального вида, которые применяются исключительно в этих областях.
Слайд 3: Трапециевидная матрица:
Трапециевидная матрица- матрица, у которой число столбцов превышает число строк, все элементы главной диагонали не равны нулю, а все элементы ниже главной диагонали равны нулю.
Слайд 4: Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1
Слайд 5: Бисимметричная матрица
В математике бисимметричная матрица — это квадратная матрица, симметричная относительно обеих диагоналей. Более точно, квадратная n × n — матрица A называется бисиметричной, если выполнены два утверждения: A = AT, AJ = JA, где J — обменная матрица n × n.
Слайд 6: Блочная матрица
Матрица размера 4×4 может быть представлена в виде блочной матрицы из четырёх блоков размера 2×2 каждый. При следующем определении блоков: блочная матрица может быть записана в таком виде:
Слайд 7: Ганкелева матрица
Квадратная матрица A порядка n называется ганкелевой матрицей , если на всех диагоналях, перпендикулярных главной, стоят равные элементы:
Слайд 8: Матрица перестановки
Матрица перестановки (или подстановки) — квадратная бинарная матрица, в каждой строке и столбце которой находится ровно один единичный элемент. Каждая матрица перестановки размера nxn является матричным представлением перестановки из n элементов.
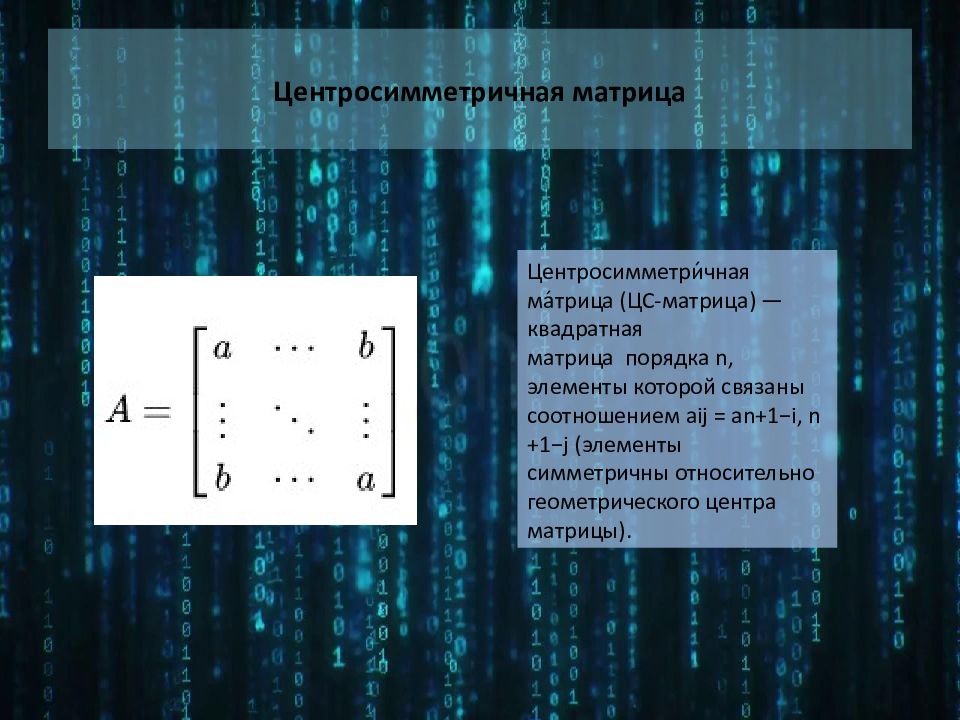
Слайд 9: Центросимметричная матрица
Центросимметри́чная ма́трица (ЦС-матрица) — квадратная матрица порядка n, элементы которой связаны соотношением aij = an+1−i, n+1−j (элементы симметричны относительно геометрического центра матрицы).