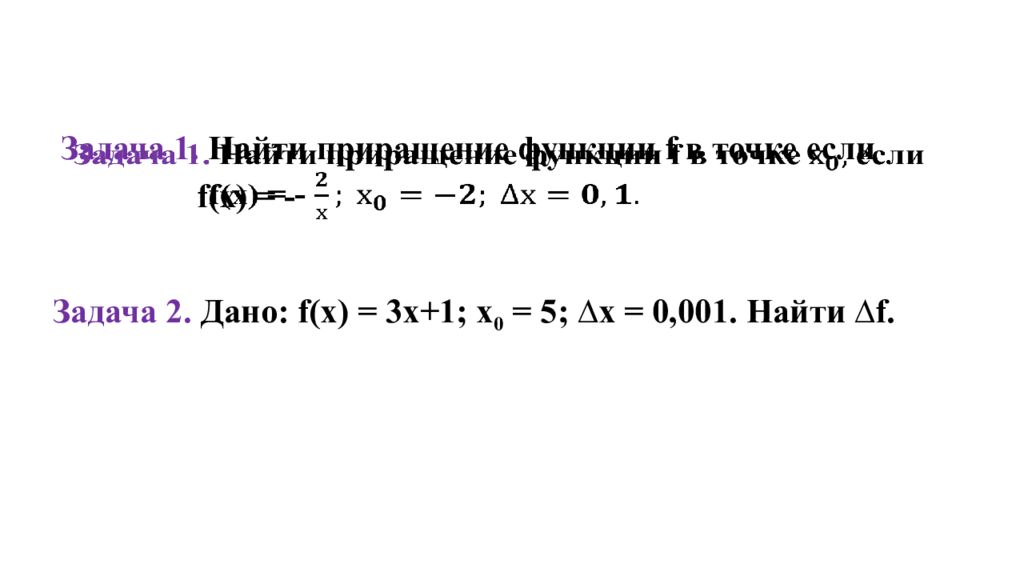ПРОИЗВОДНАЯ ФУНКЦИИ Автор: Припускова И. Г., преподаватель математики
Цель: изучить понятия приращения аргумента и функции, производной функции, правила дифференцирования; получить навыки нахождения производной функции по определению. План лекции: 1. Приращение аргумента и функции. 2. Производная. 3. Нахождение производной функции. 4. Правила дифференцирования.
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления. Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – Исаак Ньютона и Гофрид Лейбница.
Механическое истолкование производной было впервые дано И. Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени. Г. Лейбниц пришел к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной уравнением.
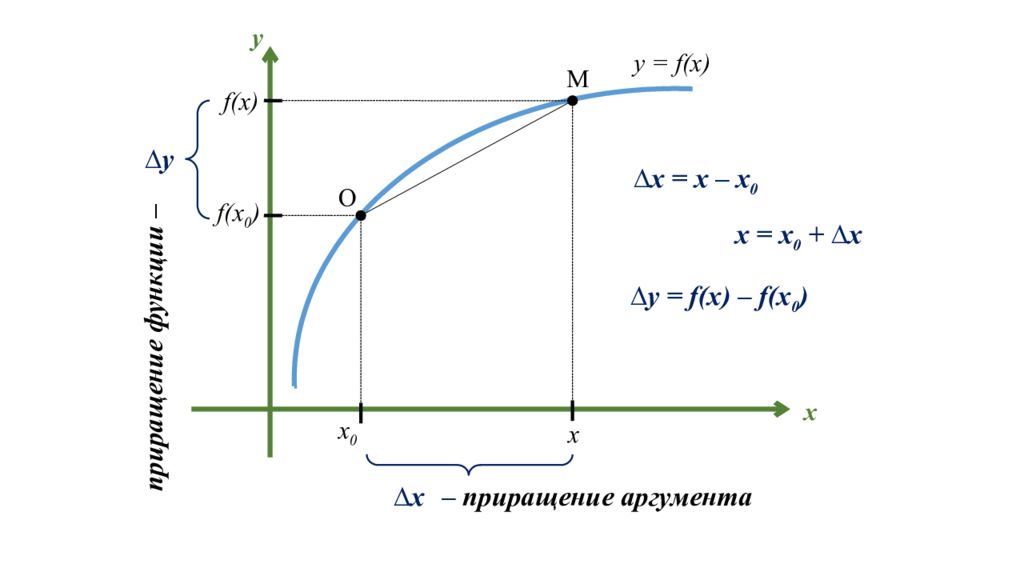
f( х 0 ) х х 0 О М f( х ) х y ∆ x ∆ y – приращение аргумента приращение функции – ∆ x = х – х 0 ∆ y = f( х ) – f( х 0 ) y = f( х ) x = х 0 + ∆х
Разность между новым значением аргумента и первоначальным называются приращение аргумента. ∆ х = х – х 0 - приращение аргумента х = х 0 + ∆х. Разность между новым значением функции и первоначальным называется приращением функции. ∆ y = f( х ) – f( х 0 ) f ( x 0 + ∆ x ) – новое значение функции ( эф от икс нулевое плюс дельта икс ). f ( x 0 ) – первоначальное значение функции. ∆ f – приращение к функции ( дельта эф ). ∆ f = f(x 0 + ∆x) – f(x 0 )
Задача 1. Найти приращение функции f в точке если f (х) = - Задача 2. Дано: f ( x ) = 3 x +1; x 0 = 5; ∆ x = 0,001. Найти ∆ f.
Определение производной Аргумент - это независимая переменная величина (х ). Функция - это зависимая переменная величина (у ). Пример. Движение характеризуют переменные величины: t – время, S - расстояние, V - скорость. t - время – это независимая величина, для математики – это аргумент. S – расстояние- это зависимая переменная величина, для математики – это функция. V - скорость при движении может быть переменной и может быть постоянной величиной.
Рассмотрим пример движения поезда. Например, поезд идет из Владивостока в Москву. Мы решили определить его скорость. Сели в Красноярске, вышли в Ачинске и говорим, что расстояние 180 км мы проехали за 3 часа. скорость поезда V = Но на этом пути было несколько остановок, когда на прямолинейном участке пути она была и 80, и 90 км/час в близи вокзалов при остановке и при отправлении была разной: и 1, и 2, и 5 и 10 (км/час). А мы говорим, что скорость поезда 60(км/час). О какой скорости идет речь?
К акая скорость называется мгновенной? Мгновенная скорость – это средняя скорость за очень маленький промежуток времени, близкий к нулю. ∆t → 0 – математические обозначения расстояние S для математики - это функция, то обозначим отрезок пути вместо ∆S знаком ∆у время t для математики - аргумент, то отрезок времени Δ t обозначим за Δх м гновенная скорость для математики является производной и обозначается у ’ или f ’ (х )
Ф ормула мгновенной скорости в математическом виде: ∆х → 0 можно считать точкой
Предел отношения приращения функции к приращению аргумента при ∆х → 0 называется производной функции f(x) в точке х 0 Штрих - обозначает действие нахождения производной Производная – это скорость изменения функции!
Действие нахождения производной называется - дифференцированием. Функция, имеющая производную, называется дифференцируемой. Другие обозначения:
ОБЩЕЕ ПРАВИЛО ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ:
Задача 3. Найти производную функции f ( х) = 5х + 3 в точке Задача 4. Дана функция f ( х) = 4 – 7х. Найдите производную f ( х). Задача 5. Дана функция f ( х) = х. Найдите производную f ( х). Задача 6. Дана функция f ( х) = х. Найдите производную f ( х). Задача 7. Дана функция f ( х) =. Найдите производную f ( х). Задача 8. Дана функция f ( х) =. Найдите производную f ( х). производная степенной функции ( x n ) ′ = nx n -1 Задача 9. Дана функция f ( х) = 9. Найдите производную f ( х).
ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 1) 2) 3) 4) 5) СТЕПЕННЫЕ ФУНКЦИИ
ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 6) 7) 8) 9) 10) ПОКАЗАТЕЛЬНЫЕ ФУНКЦИИ ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 11) 12) 13) 14) ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Самостоятельная работа ВАРИАНТ 1 1. Найдите приращение функции f в точке х 0, если f (х) = 2х 2 – 3, х 0 = 3 и Δх = - 0,2. 2. Пользуясь определением производной, найдите производную функции f (х) = х 2 – 3х. ВАРИАНТ 2 1. Найдите приращение функции f в точке х 0, если f (х) = 3х + 1, х 0 = 5 и Δх = 0,01. 2. Пользуясь определением производной, найдите производную функции f (х) = 4 - х 2.
