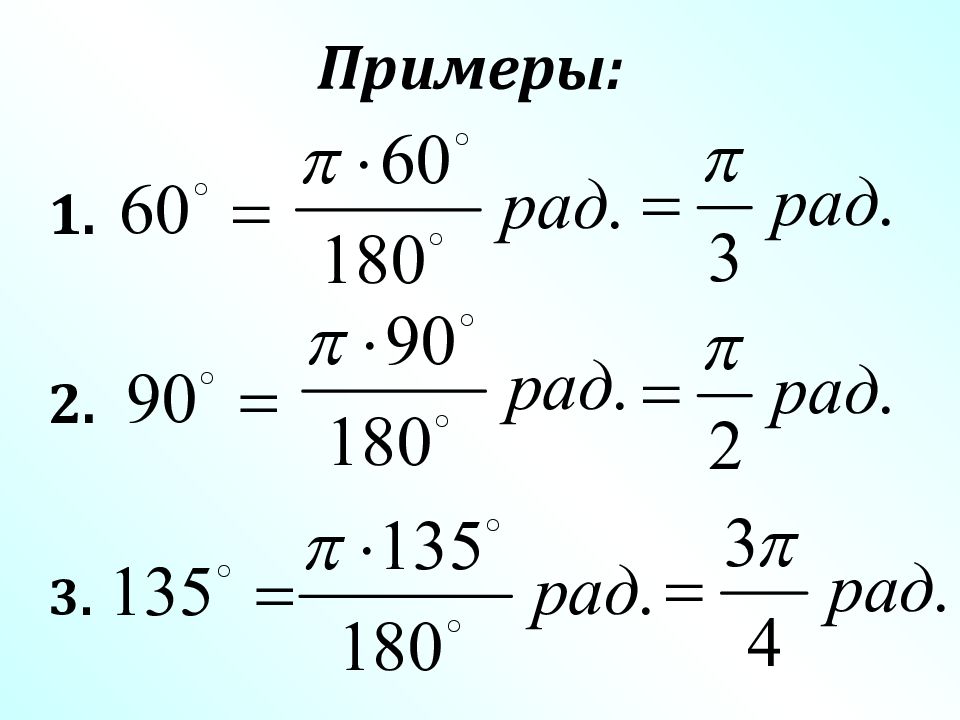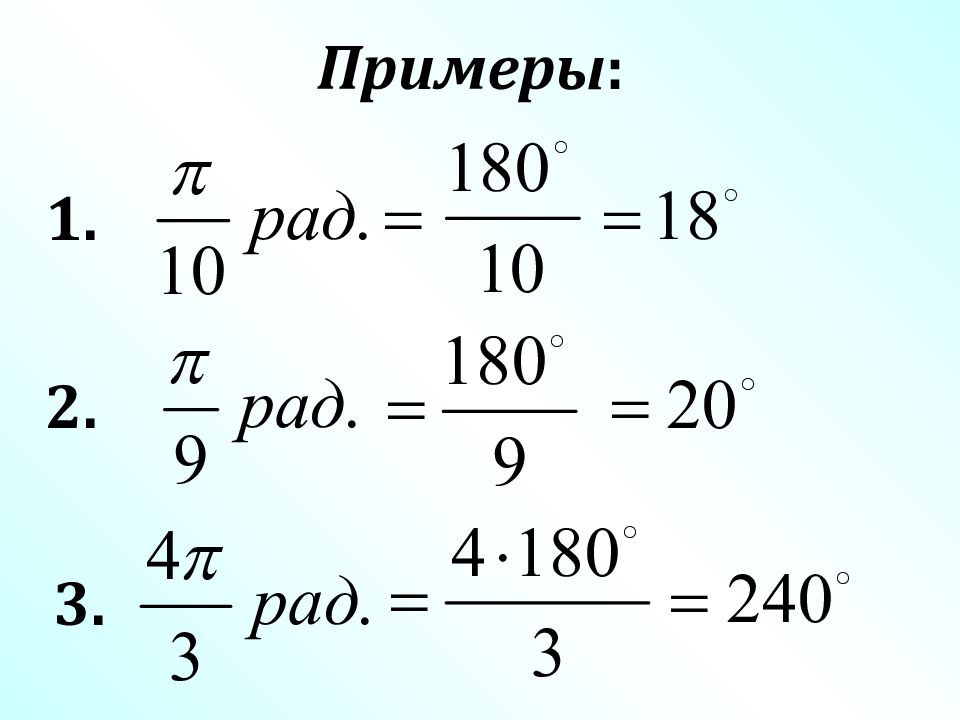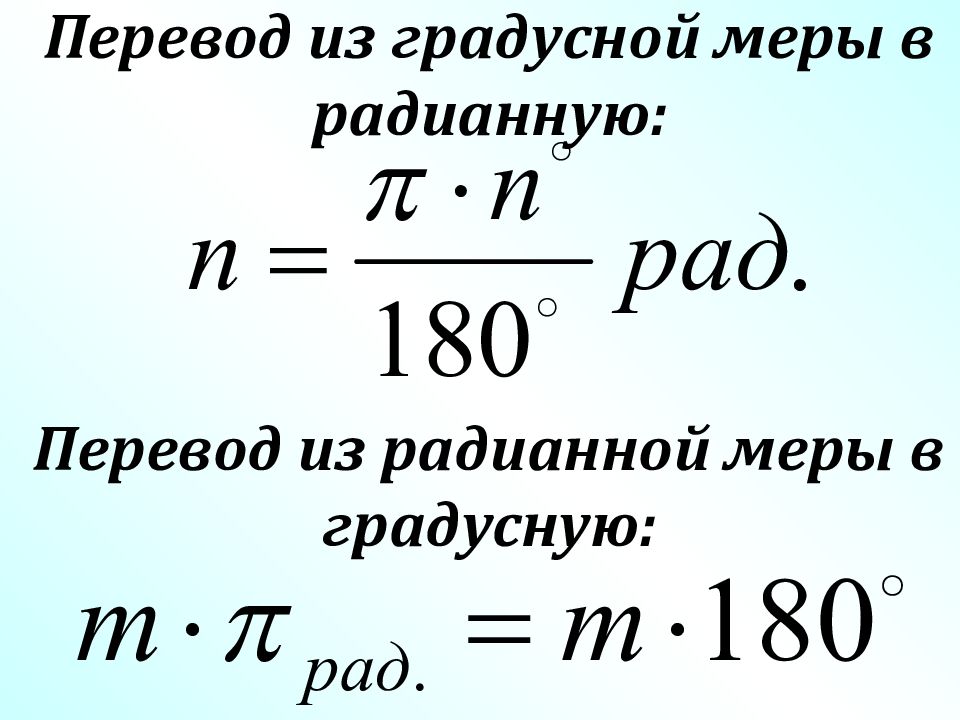Слайд 2
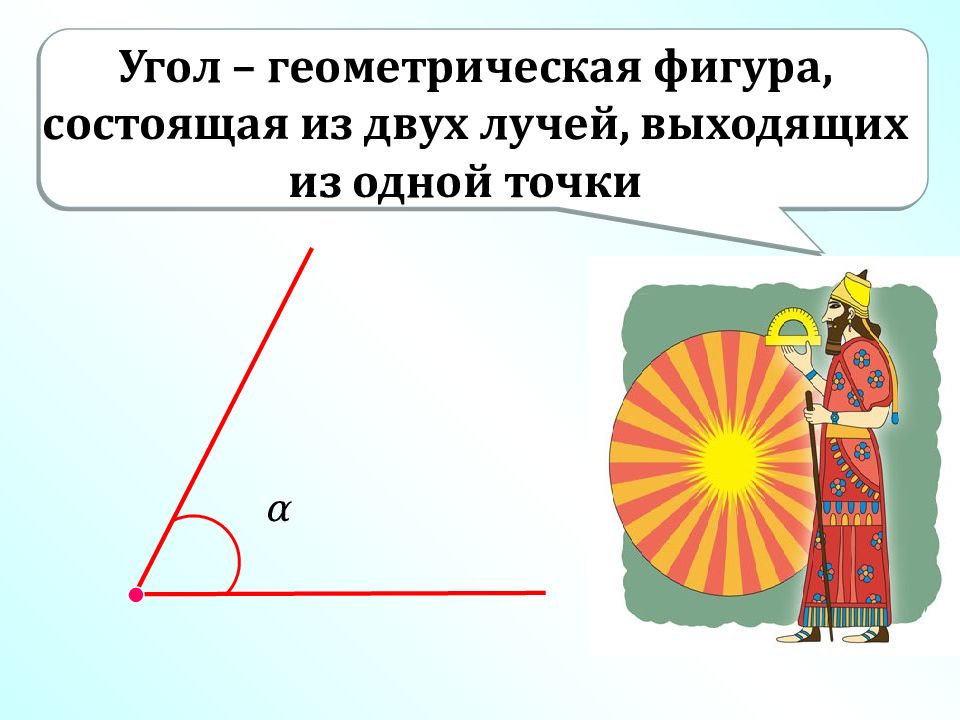
Угол – геометрическая фигура, состоящая из двух лучей, выходящих из одной точки α
Слайд 3: Измерение углов
Слайд 4
Единицы измерения угла: 1 минута ( 1 ’) - часть градуса 1 секунда ( 1 ’’) - часть минуты
Слайд 5
Вавилоняне считали, что за каждые сутки солнце делало один «шаг», поэтому разделили окружность на 360 равных частей, каждую из которых называют градусом (от лат. gradus — шаг, ступень).
Слайд 6
Развитие тригонометрии вызвало необходимость в 19 веке введения новой меры измерения углов- радианной.
Слайд 7
Измерение углов 1 радиан ( от латинского radius - спица колеса) - центральный угол, длина дуги которого равна радиусу окружности
Слайд 8
Число Пи – математическая константа, которая выражает отношение длины окружности к её диаметру
Слайд 14
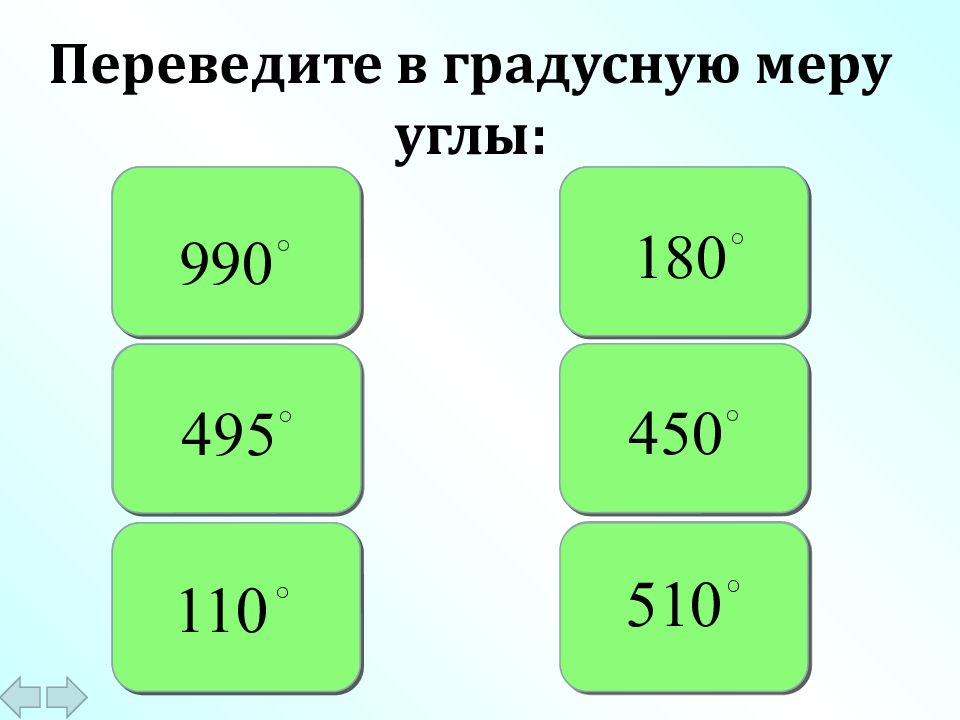
Переведите в радианную меру углы: 45 10 36 240 150 330 180 270 360 2
Слайд 19
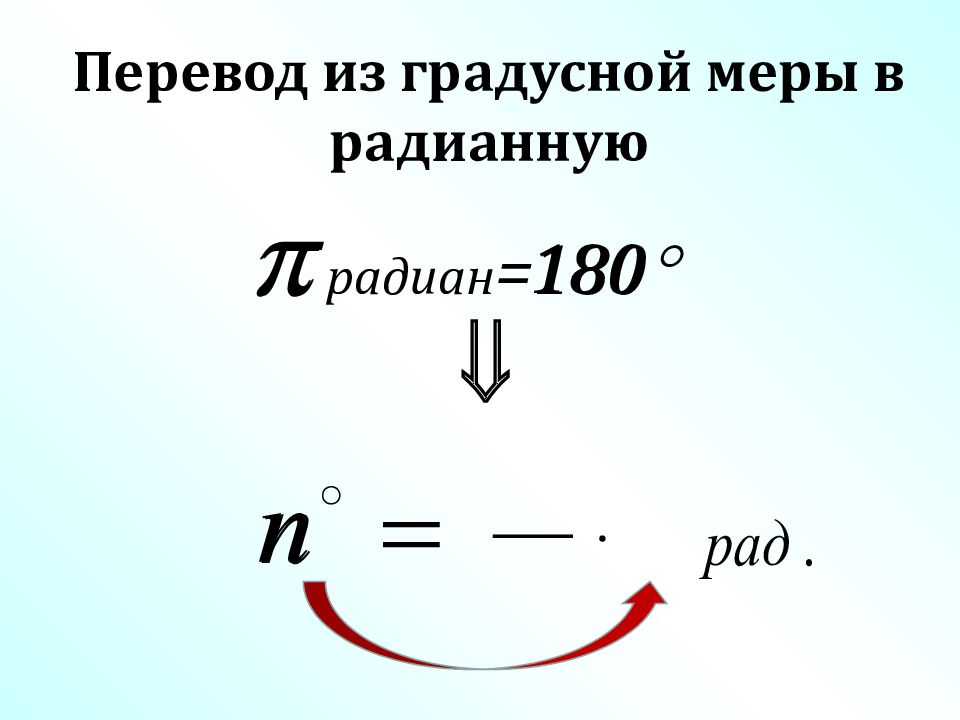
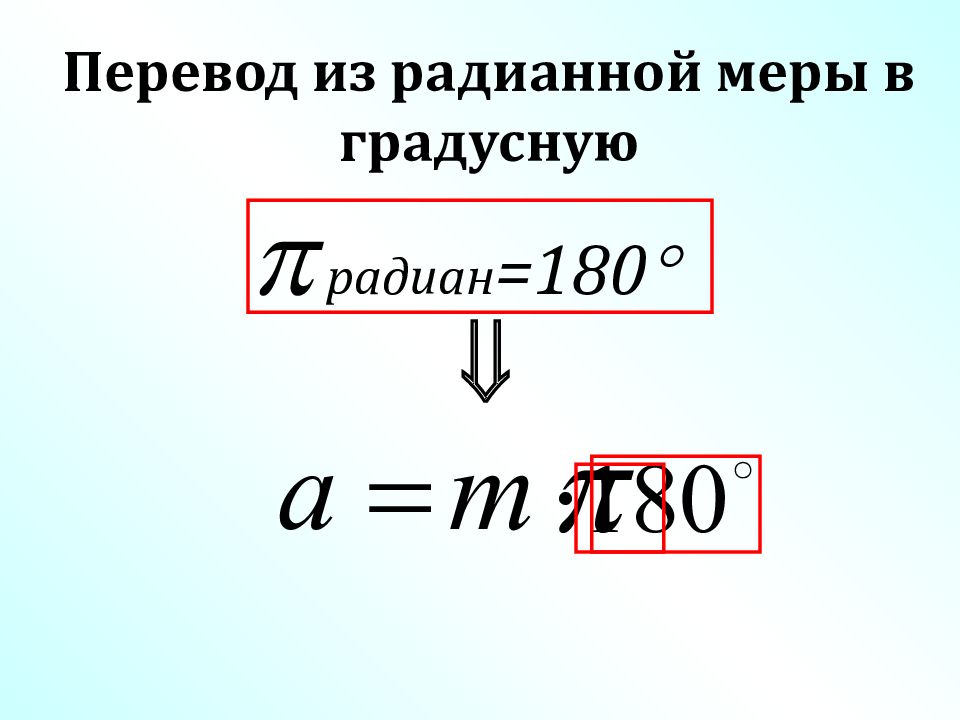
Перевод из градусной меры в радианную: Перевод из радианной меры в градусную:
Слайд 20
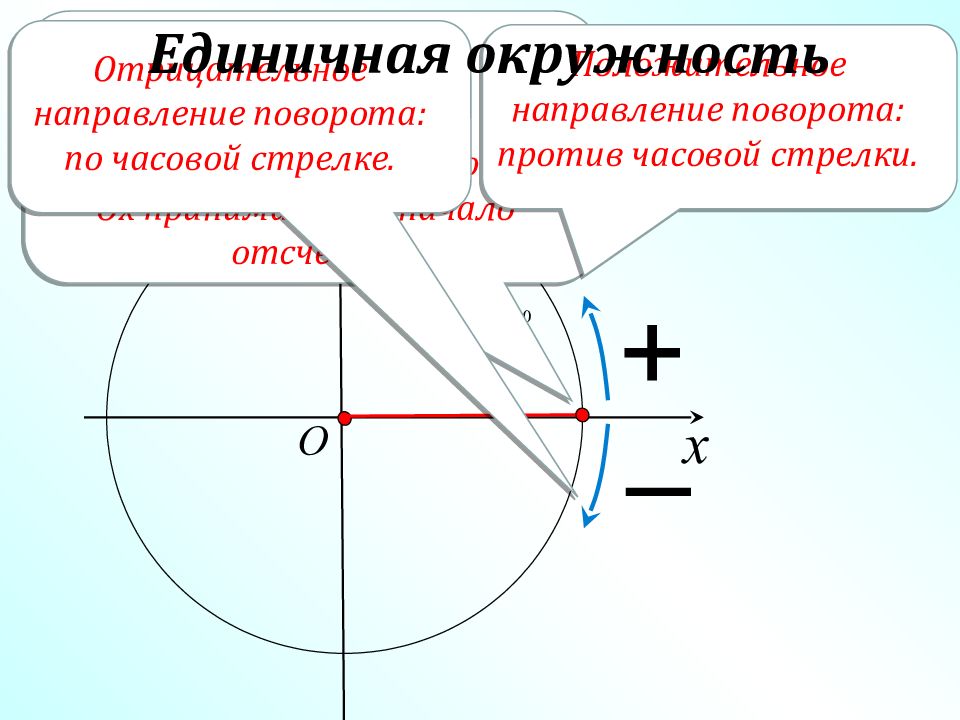
x y O + – Окружность с центром в начале системы координат Oxy и радиусом, равным единице, называется единичной, а ограниченный ей круг – тригонометрическим. Точку пересечения окружности с положительной частью оси Ох принимают за начало отсчета Положительное направление поворота: против часовой стрелки. Отрицательное направление поворота: по часовой стрелке. Единичная окружность
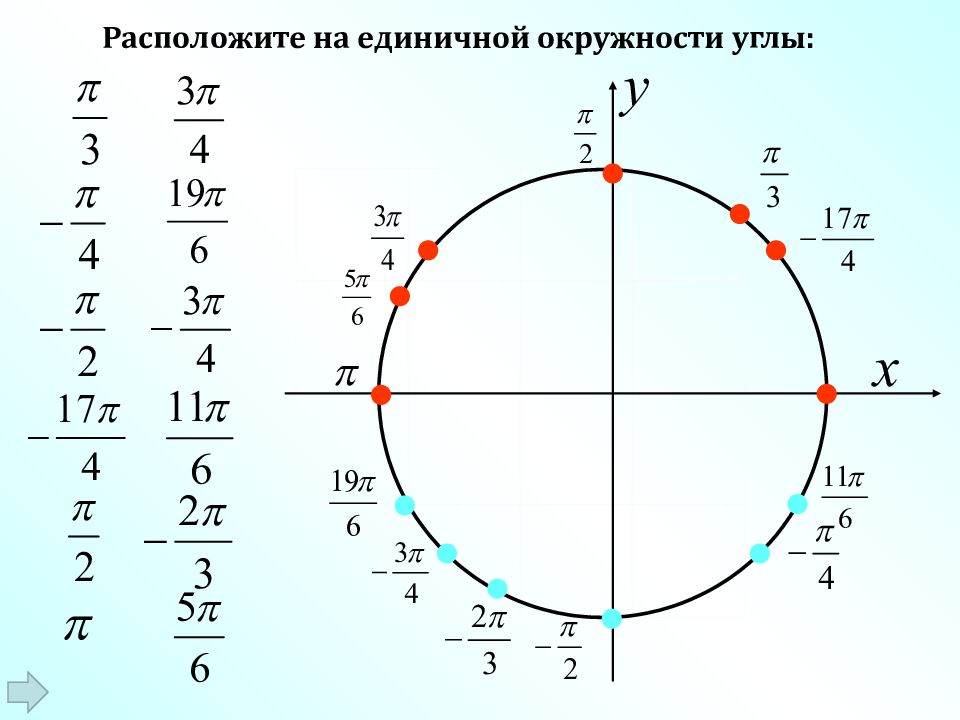
Слайд 21
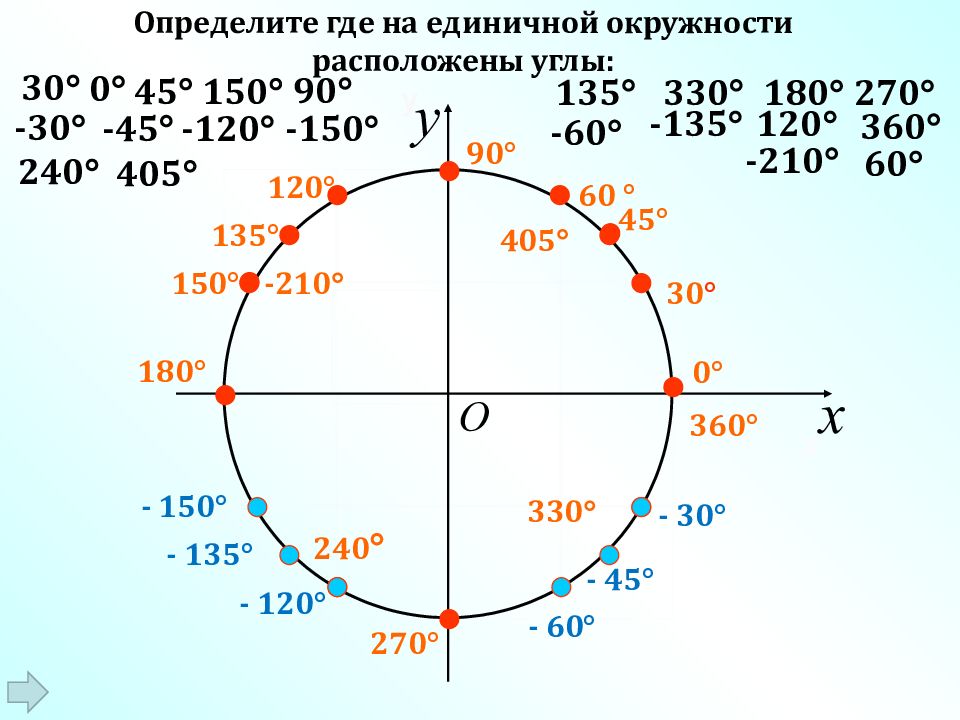
45 -60 135 240 150 Х у 0 ° 180 ° 30 ° 60 ° 90 ° 270 ° 45° - 30 ° - 45 ° - 60 ° 150 ° 135 ° 120 ° - 120 ° - 135 ° - 150 ° x y O Определите где на единичной окружности расположены углы: 0 30 60 90 180 330 240 270 330 -30 -45 -120 -150 120 360 -135 -210 -210 405 405 360 °
Слайд 23
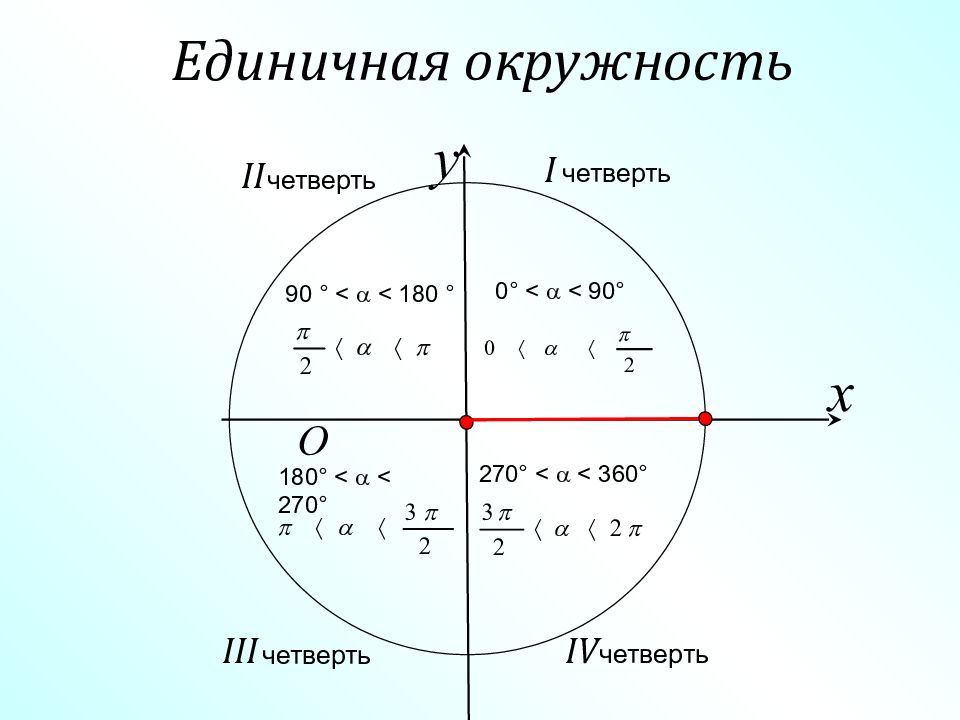
x y O III 0 ° < < 90 ° 90 ° < < 180 ° 180 ° < < 270 ° 270 ° < < 360 ° I II IV четверть четверть четверть четверть Единичная окружность
Слайд 24
x y O Определите, в какой четверти расположены углы: = 25 ° = = 220 ° = I четверть четверть III III четверть четверть II
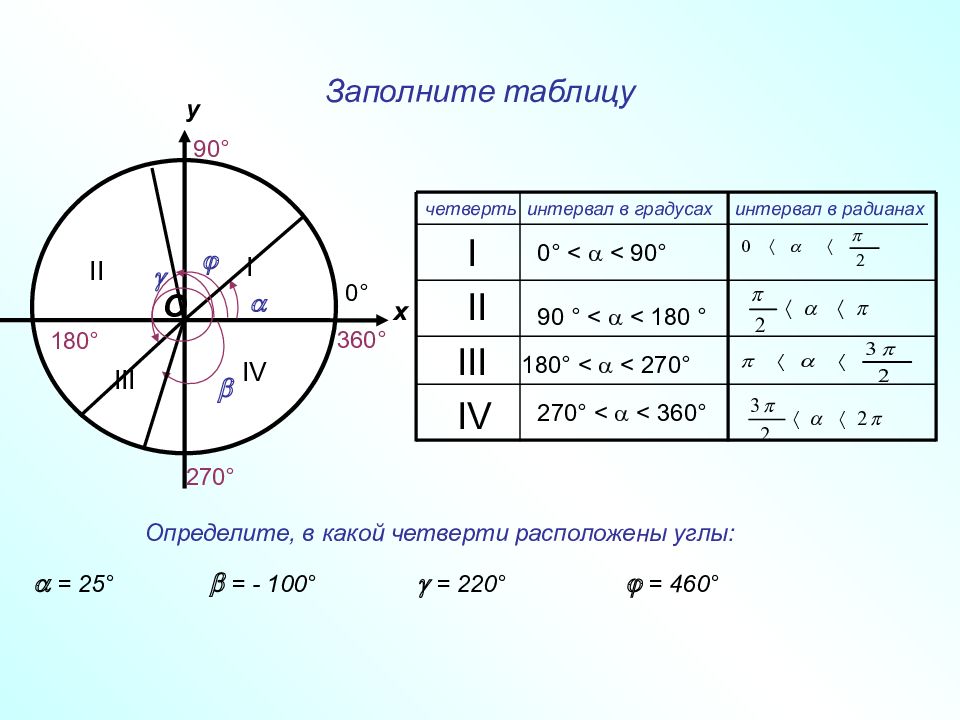
Слайд 25: Заполните таблицу
у О х 90 ° 270 ° 180 ° 0 ° 360 ° IV III II I интервал в градусах четверть 0 ° < < 90 ° 90 ° < < 180 ° 180 ° < < 270 ° I II IV III Определите, в какой четверти расположены углы: = 25 ° = - 100 ° = 460 ° = 220 ° интервал в радианах 270 ° < < 360 °
Последний слайд презентации: Радианная мера угла Угол поворота
Самостоятельная работа 1. Переведите в радианную меру углы, определите в какой четверти они расположены: 1) 60 2) 145 3) 240 I вариант II вариант 1) 320 2) 105 3) 40 2. Переведите в градусную меру углы, определите в какой четверти они расположены: 1) 2) 1) 2)