Первый слайд презентации: Тема: Вычисление производной
Урок 40-41 Повторение пройденного: ? Записать наизусть формулы производных 1. Постоянной функции 2 Линейной функции 3 Степенной функции Правило вычисления: (с· х )´= Обратной функции (1/ х )´= У= ( √х )´=
Слайд 2: Определение производной
Математический анализ, созданный Ньютоном и Лейбницем, долго развивался на основе понятия производной как «скорости изменения функции».
Слайд 3: Самопроверка
0 35 -6 ¼ 1/ √х -1/ х ² 8х 0 -1 1 11. 3х² (Устный счет) Найти производные: 132´= (35· х )´= (1-6х)´= (¼· х+ 21)´= (2√х+1)´= (1/ х +3)´= (4· х ²)´= (-0,25)´= (-х+2)´= (х+26)´=
Слайд 4: Самопроверка
0 -5 1/ х ² х /2 4/ √х -9/ х ² 28х 0 -7 1 11. ( Игра-1 : «Кто быстрей?») Найти производные: (-1/12)´= (-5· х )´= (8-1/ х )´= (¼· х²+ 2)´= (8√х+ ⅓ )´= (9/ х +73)´= ( 1 4· х ²)´= (-0,265)´= (-7х+92)´= (х-6)´=
Слайд 5: Закрепление пройденного
Задание. Решение. Вычислить производную функции у=х³+2х²-6 в данной точке х 0= 2. 1) у´= (х³+2х²-6)´= 2) у´(х 0 )= у´(2)= Ответ: у´(2)=20
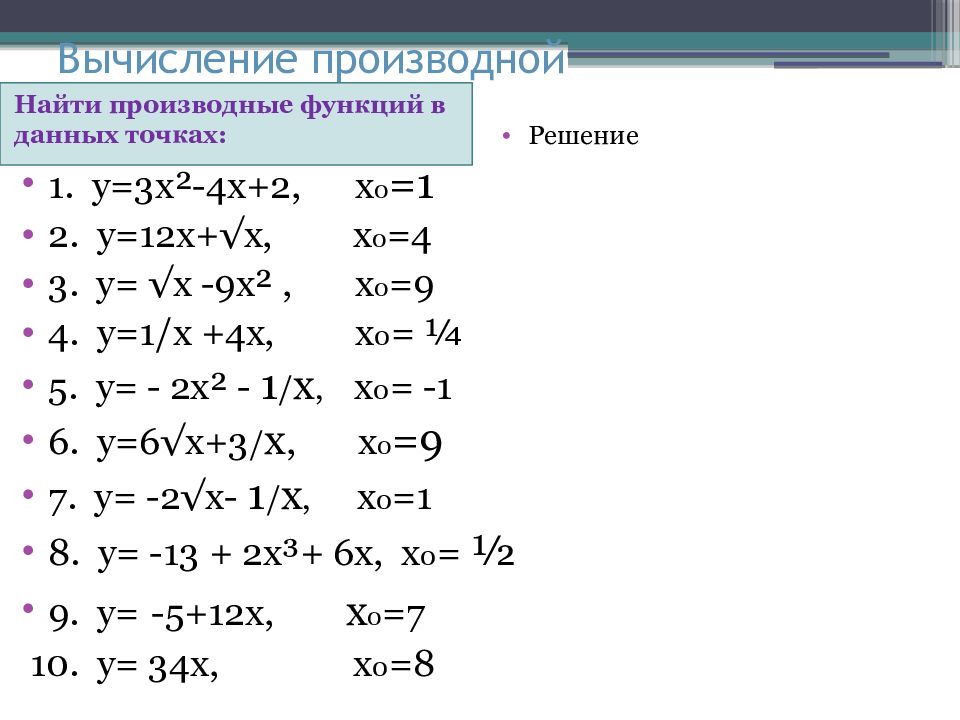
Слайд 6: Вычисление производной
Найти производные функций в данных точках: 1. у=3х²-4х+2, х 0 =1 2. у=12х+√х, х 0 =4 3. у= √х -9х², х 0 =9 4. у=1/ х +4х, х 0 = ¼ 5. у= - 2х² - 1 / х, х 0 = -1 6. у=6√х+3 / х, х 0 =9 7. у= -2√х- 1 / х, х 0 =1 8. у= -13 + 2х³+ 6х, х 0 = ½ 9. у= -5+12х, х 0 =7 10. у= 34х, х 0 =8 Решение
Слайд 7: Вычисление производной
Найти производные функций в данных точках: 1. у=3х²-4х+2, х 0 =1 2. у=12х+√х, х 0 =4 3. у= √х -9х², х 0 =9 4. у=1/ х +4х, х 0 = ¼ 5. у= - 2х² - 1 / х, х 0 = -1 Решение
Слайд 8: Вычисление производной
Найти производные функций в данных точках: Ответы для самопроверки 1. у=3х²-4х+2, х 0 =1 2. у=12х+√х, х 0 =4 3. у= √х -9х², х 0 =9 4. у=1/ х +4х, х 0 = ¼ 5. у= - 2х² - 1 / х, х 0 = -1 6. у=6√х+3 / х, х 0 =9 7. у= -2√х- 1 / х, х 0 =1 8. у= -13 + 2х³+ 6х, х 0 = ½ 9. у= -5+12х, х 0 =7 10. у= 34х, х 0 =8 1. у(х 0 )=2 2. у(х 0 )=12,25 3. у(х 0 )=- 161,8 4. у(х 0 )=- 12 5. у(х 0 )=5 6. у(х 0 )=26/27 7. у(х 0 )=0 8. у(х 0 )=7,5 9. у(х 0 )=12 10. у(х 0 )=34